运筹系列65：TSP问题的精确求解法概述

Posted 2023-03-05 IE06

1. 给定upbound的Christofides方法

这是可以给出上界的一个方法，可以证明构造出的路线不超过最优路线的1.5倍。步骤为：
1）构造MST（最小生成树）
2）将里面的奇点连接起来构成欧拉回路称为完美匹配。Edmonds给出了多项式时间内构造最小代价完美匹配的方法，其长度不超过最优解的1.5倍。

证明方法也很直观，奇点最短路径可以拆分成两条完美匹配，其中总有一条的长度$\le$最优奇点路径长度/2$\le$最优完整路径长度/2

3）按欧拉回路顺序逐个扫描点，跳过重复经过的点，即可构造一条完整的路径。

2. 给定lowerbound的松弛问题

首先看一个例子：

我们定义$x_{ij}$为边ij是否在路径上。根据TSP问题的要求，每个点只能路过一次，因此每个点连着两条边，有：

3. 割平面法

3.1 子回路约束

如下图，上面的模型无法避免subtour

为了消除两个子路径的情形，再增添约束条件：

要想完全枚举出所有这样的约束条件很难，在城市数目为10时，不等式数目就达到51043900866个。因此我们常采用行生成（也叫割平面）的方法，从松弛问题开始，每次求解完后，若发现有子路径，则不断增添拆散子路径的约束条件即可。示意如下，其中红色表示0.5，黑色表示1：

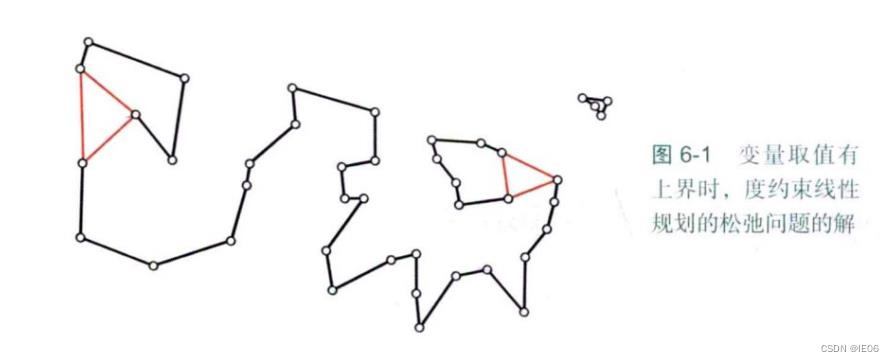
3.2 梳子约束

接下来，为了取整，我们再添加4集合约束：


后面逐步增加个数，称为梳子不等式，每条回路穿过边界的数目至少是3k+1次，其中k是梳齿的数目。

4. 行生成算法

4.1 生成子回路约束

如上图，我们随意选定两个点，得到它们之间的最大流，这个值等于最小割。因此，我们计算n-1个最大流，如果得到小于2的值，那么找到对应的最小割加入约束集。

4.2 生成梳子约束

使用启发式方法，如下图，对每个红色子图构造梳子约束：

生成梳子的研究可以参考：

Sylvia Boyd/Sally Cockburn/ Danielle Vella
Daniel Espinoza/Marcos Goycoolea

4.3 blossom不等式

可以看作subtour约束的加强版。选取顶点数目为奇数的簇，完美匹配中至少有一条边穿过簇的边界（相对应的，subtour约束的右边是2）。

5. 分枝定界

如果只用subtour约束，我们可以结合分枝定界算法来处理整数约束条件：

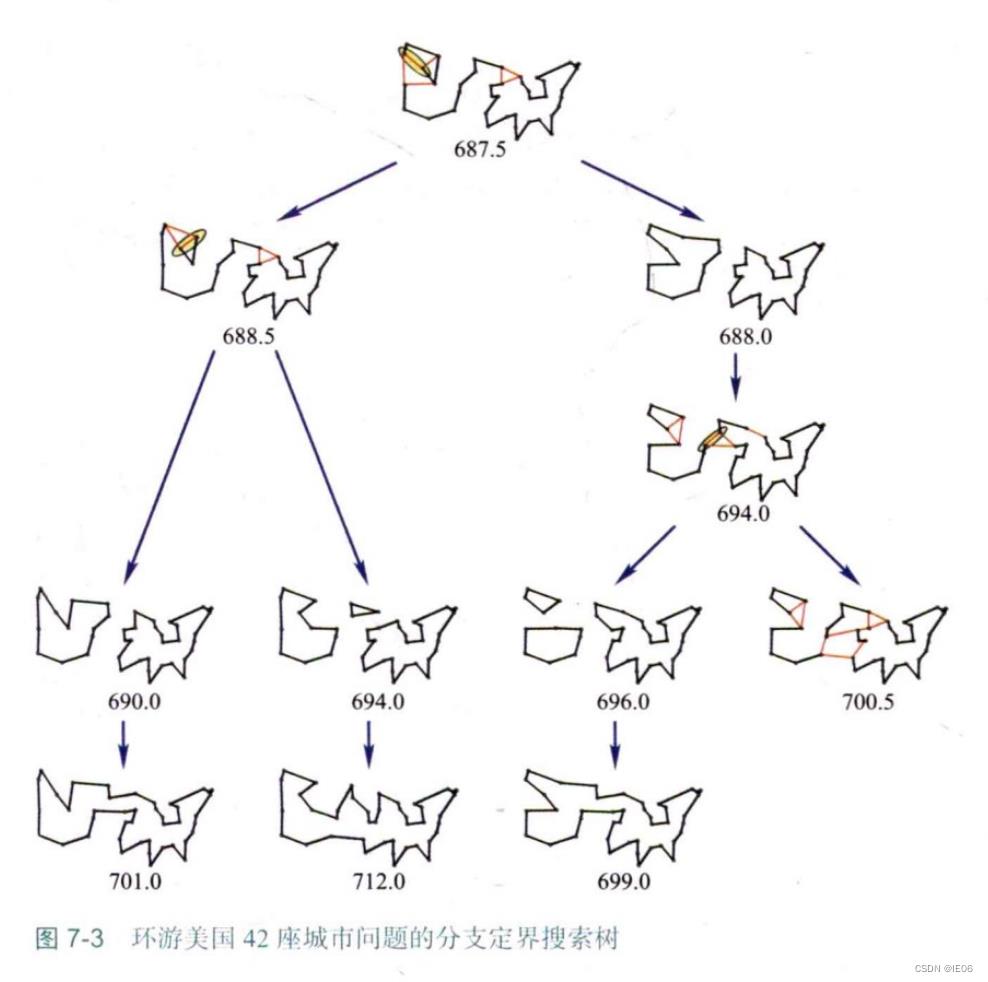
分枝定界的关键是如何快速确定下界，否则膨胀速度会非常快。因此将其与分割法结合起来，得到新的分枝切割法。