TSP问题基于禁忌搜索算法求解TSP问题

Posted 2021-06-30 MatlabQQ1575304183

文章目录

• 一、TSP问题概述
• 二、禁忌搜索算法
• • 1、基本原理
  • 2、参数设置
  • 3、算法特点
  • 4、算法流程
• 三、MATLAB程序实现
• • 1、问题描述
  • 2、禁忌搜索算法求解
  • 3、仿真结果

一、TSP问题概述

旅行商问题(traveling salesman problem,TSP)又称为推销员问题、货郎担问题，该问题是最基本的路线问题。该问题寻求单一旅行者由起点出发，通过所有给定的需求点之后，最后再回到起点的最小路径成本。最早的旅行商问题的数学模型是由Dantzig(1959)等人提出的。旅行商问题是车辆路线问题(VRP)的特例，已证明旅行商问题是NP难题。

二、禁忌搜索算法

1、基本原理

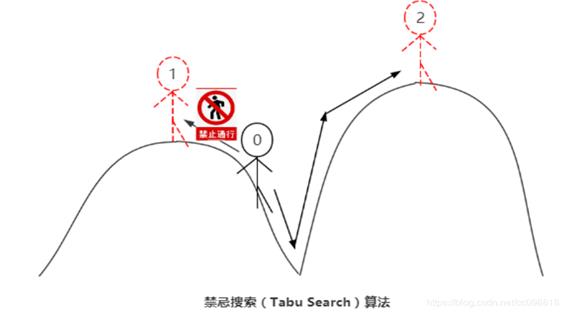
标记已经解得的局部最优解或求解过程，并在进一步的迭代中避开这些局部最优解或求解过程。局部搜索的缺点在于，太过于对某一局部区域以及其邻域的搜索，导致一叶障目。为了找到全局最优解，禁忌搜索就是对于找到的一部分局部最优解，有意识地避开它，从而或得更多的搜索区域。

比喻：兔子们找到了泰山，它们之中的一只就会留守在这里，其他的再去别的地方寻找。就这样，一大圈后，把找到的几个山峰一比较，珠穆朗玛峰脱颖而出。

2.2 算法过程

step1：给以禁忌表H=空集，并选定一个初始解xnow；

step2：满足停止规则时，停止计算，输出结果；否则，在xnow的邻域N(xnow)中选择不受禁忌的候选集Can_N(xnow)；在Can_N(xnow)中选一个评价值最佳的解xnext，xnow=xnext；更新历史记录H，保存f(xnow)，重复step2；

step3：在保存的众多f中，挑选最小（大）值作为解；

1. 兔子们找到了泰山，它们之中的一只就会留守在这里，其他的再去别的地方寻找。当兔子们再寻找时，一般地会有意识地避开泰山，因为他们知道，这里已经找过，并且有一只兔子在那里看着了。这就是禁忌搜索中“禁忌表(tabulist)”的含义。

2. 那只留在泰山的兔子一般不会就安家在那里了，它会在一定时间后重新回到找最高峰的大军，因为这个时候已经有了许多新的消息。这个归队时间，在禁忌搜索里面叫做“禁忌长度(tabu length)”;

3. 如果在搜索的过程中，留守泰山的兔子还没有归队，但是找到的地方全是华北平原等比较低的地方，兔子们就不得不再次考虑选中泰山，泰山毕竟也有一个不错的高度，也就是说，当一个有兔子留守的地方优越性太突出，超过了“best so far”“的状态，就可以不顾及有没有兔子留守，都把这个地方考虑进来，这就叫“特赦准则(aspiration criterion)”

这三个概念就是禁忌搜索和一般搜索准则最不同的地方，算法的优化也关键在这里。

构成要素

1. 评价函数 (Evaluation Function):评价函数是用来评价邻域中的邻居、判断其优劣的衡量指标。大多数情况下，评价函数为目标函数。但自定义的形式也可存在，算法也可使用多个评价函数，以提高解的分散性（区分度）。

2. 邻域移动（Move Operator）：邻域移动是进行解转移的关键，又称“算子”，影响整个算法的搜索速度。邻域移动需要根据不同的问题特点来自定义，而整个邻近解空间是由当前解通过定义的移动操作构筑的所有邻域解构成的集合。

3. 禁忌表（Tabu Table）：禁忌表记录被禁止的变化，以防出现搜索循环、陷入局部最优。对其的设计中最关键的因素是禁忌对象（禁忌表限定的对象）和禁忌步长（对象的禁忌在多少次迭代后失效）禁忌表是禁忌搜索算法的核心，禁忌表的对象、步长及更新策略在很大程度上影响着搜索速度和解的质量。若禁忌对象不准确或者步长过小，算法避免陷入局部最优的能力会大打折扣；若禁忌表步长过大，搜索区域将会限制，好的解就可能被跳过。)。

4. 禁忌长度：禁忌表中所能接受的最多禁忌对象的数量。

5. 禁忌步长：对象的禁忌在多少次迭代后失效。

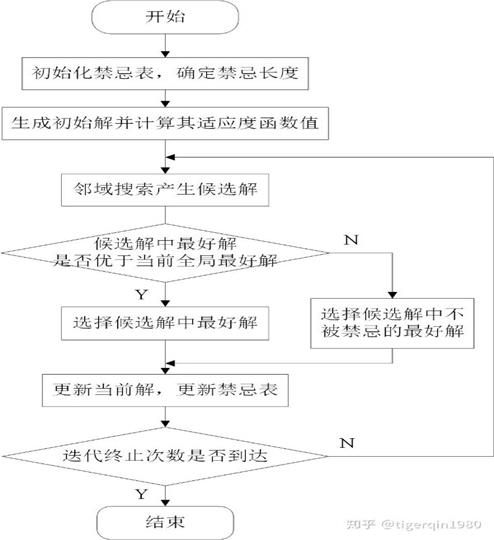
算法流程

图1 TS算法的流程图

三、MATLAB程序实现

1、问题描述

假设有意旅行商要拜访全国31个省会城市（不包括港澳台），从一个城市出发，需要经过，所有城市后，回到出发地。每个城市只能经过一次，要求选择一个最短路径。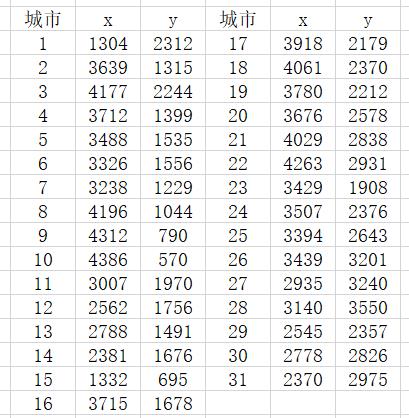

表1 各个城市的坐标

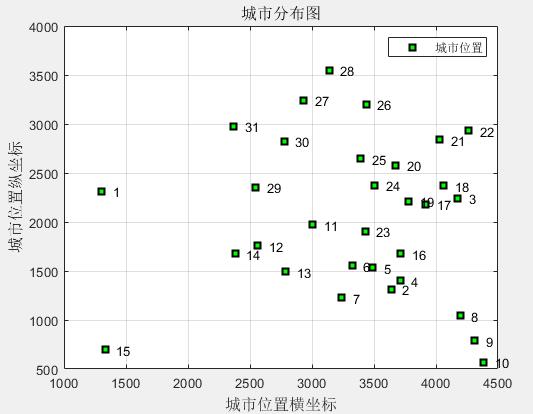
图2 31个城市分布图

2、禁忌搜索算法求解

（1）初始化参数、置空禁忌表。初始化城市规模n=31，禁忌长度TabuL=22，候选解的个数Ca=200，最大迭代次数iter_max=1000，citys表示31个城市的坐标等参数。代码如下：

load citys_data.mat;
n = size(citys, 1);                   % 城市数目
D = zeros(n);                         % 距离矩阵
Tabu = zeros(n);                      % 禁忌表
TabuL = round(sqrt(n*(n-1)/2));       % 禁忌长度
Ca = 200;                             % 候选集的个数(全部邻域解个数)
Canum = zeros(Ca, n);                 % 候选解集合
S0 = randperm(n);                     % 随机产生初始解
bestsofar = S0;                       % 当前最佳解
BestL = Inf;                          % 当前最佳解距离
iter = 1;                             % 初始迭代次数
iter_max = 1000;                      % 最大迭代次数

%% 计算距离矩阵
for i = 1:n
    for j = i+1:n
        D(i, j) = sqrt(sum((citys(i, :)-citys(j, :)).^2));
        D(j, i) = D(i, j);
    end
end

（3）定义初始解的邻域映射为2-opt形式，即初始解路径中随机交换两个城市。代码如下：

i = 1;
A = zeros(Ca,2);            % 交换的城市矩阵，200行2列
%% 求邻域解中交换的城市矩阵
% 将一个200行2列的A阵用随机的方式填满，且没有任意两组数是相等的
while i <= Ca
    r = ceil(n*rand(1,2));         % 随机交换两个城市
    if r(1) ~= r(2)
        A(i, 1) = max(r(1), r(2));
        A(i, 2) = min(r(1), r(2));
        if i == 1
            flag = 0;
        else
            for j = 1:i-1
                if A(i, 1) == A(j, 1) && A(i, 2) == A(j, 2)
                    flag = 1;
                    break;
                else
                    flag = 0;
                end
            end
        end
        if ~flag
            i = i + 1;
        end
    end
end
%% 产生邻域解
% 保留前BestCanum个最好候选解
BestCanum = Ca/2;
BestCa = Inf * ones(BestCanum, 4);
F = zeros(1, Ca);
for i = 1:Ca
    Canum(i, :) = S0;
    Canum(i, [A(i, 2), A(i, 1)]) = S0([A(i, 1), A(i, 2)]);  % 交换A(i, 1)和A(i, 2)列的元素
    F(i) = fitness(D, Canum(i, :));
    if i <= BestCanum    % 选取候选集
        BestCa(i, 1) = i;       % 第1列保存序号
        BestCa(i, 2) = F(i);   % 第2列保存适应度值(路径距离)
        BestCa(i, 3) = S0(A(i, 1));     % 第3列保存交换后的数据
        BestCa(i, 4) = S0(A(i, 2));     % 第4列保存交换后的数据
    else
        for j = 1:BestCanum   % 更新候选集
            if F(i) < BestCa(j, 2)
                BestCa(j, 1) = i;
                BestCa(j, 2) = F(i);
                BestCa(j, 3) = S0(A(i, 1));
                BestCa(j, 4) = S0(A(i, 2));
                break;
            end
        end
    end
end
% 对候选集按照适应度值进行升序排列
[value, index] = sort(BestCa(:, 2));
SBest = BestCa(index, :);
BestCa = SBest;                     % 选取前100个比较好的候选解

（4）判断选出的解是否满足特赦准则。代码如下：

%% 特赦准则
if BestCa(1,2) < BestL     % 候选解比最佳值都还小，那么不管在不在禁忌表中，都是一样的操作
    % 在禁忌表中，全部减1，特赦出来，放在最后；
    % 不在禁忌表中，全部减1，放在最后；
    BestL = BestCa(1, 2);               % BestL当前最优解适配值
    S0 = Canum(BestCa(1,1), :);     % 最优解的替换
    bestsofar = S0;
    % 更新禁忌表
    for i = 1:n
        if Tabu(i, :) ~= 0
            Tabu(i, :) = Tabu(i, :)-1;
        end
    end
    Tabu(BestCa(1, 3), BestCa(1, 4)) = TabuL;         % 更新禁忌表，把特赦的这个放在最末端
else                 % 候选解中最佳的解 仍然没有比目前最佳值更优，则：
    for i = 1:BestCanum                        % 遍历候选集
        if Tabu(BestCa(i, 3), BestCa(i, 4)) == 0  % BestCa就是从小到大排列的，选取第一个不在禁忌表中的解，即禁忌长度为0
            S0 = Canum(BestCa(i, 1), :);         % 则释放，并作为下一次迭代的初始解
            for j = 1:n
                if Tabu(j, :) ~= 0
                    Tabu(j, :) = Tabu(j, :)-1;
                end
            end
            Tabu(BestCa(i, 3), BestCa(i, 4)) = TabuL;   % 放到禁忌表最末端
            break;  %  立刻跳出for循环，因为已经选中不在禁忌表中的最佳解了
        end
    end
end

3、仿真结果

​

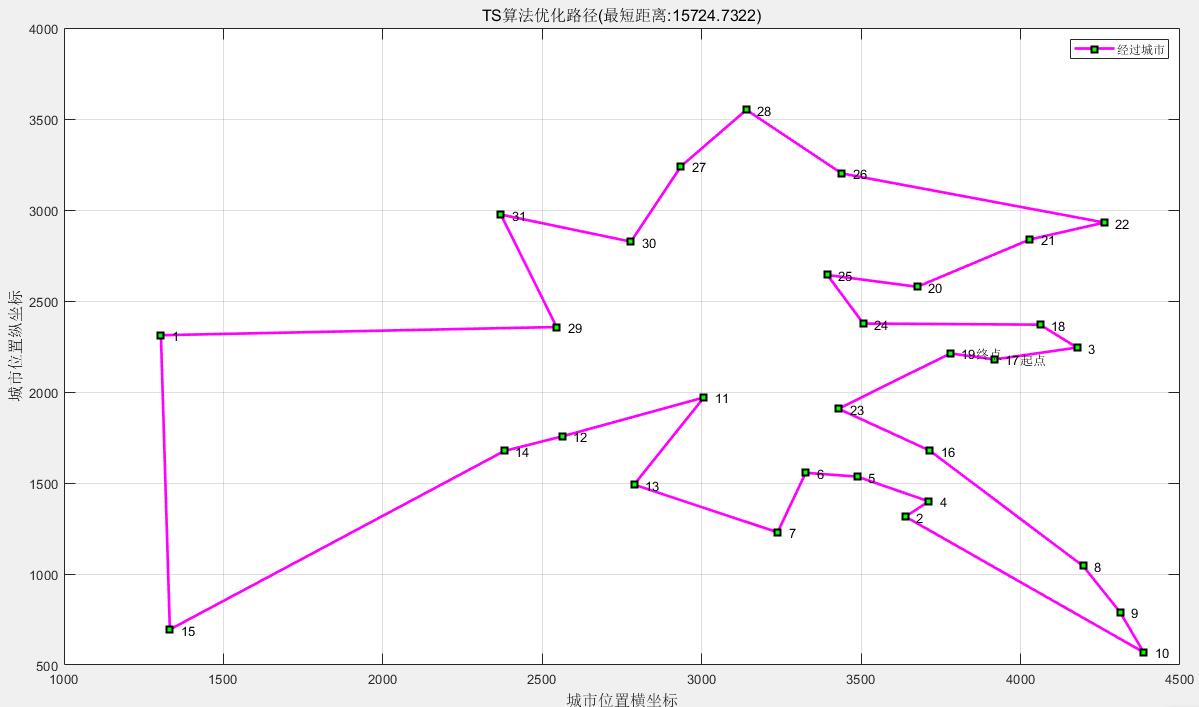
图3 TS算法优化路径

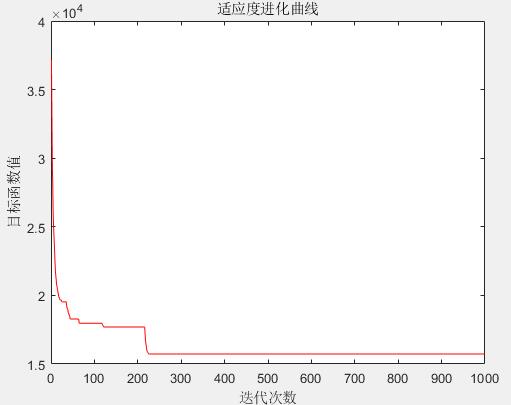
图4 适应度进化曲线

代码下载或者仿真咨询添加QQ1575304183