js数据结构可逐次添加叶子的二叉树（非最优二叉树）

Posted 2020-09-09 卡迪斯上小学

最近小菜鸟西瓜莹看到了一道面试题：

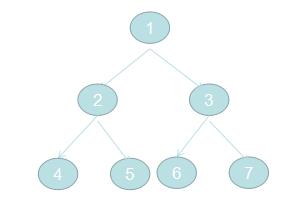
　　给定二叉树，按层打印。例如1的子节点是2、3， 2的子节点是3、4， 5的子节点是6，7.

　　需要建立如图二叉树：

 

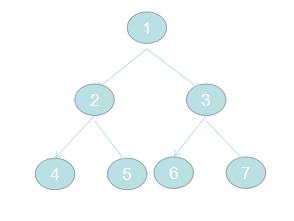
　　但是西瓜莹找到的相关代码都是用js构建最优二叉树，假如，依次向二叉树中添加4，2，6，1，3，5，7最优二叉树如图：

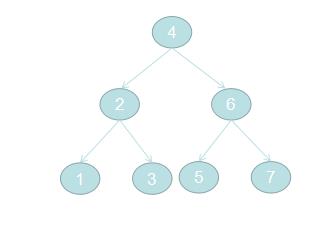
　　比根节点小的节点总是放在根节点的左节点上，比根节点大的节点总是放在根节点的右节点上。

　　假如想依次向二叉树添加1，2，3，4，5，6，7 二叉树又是如何呢？

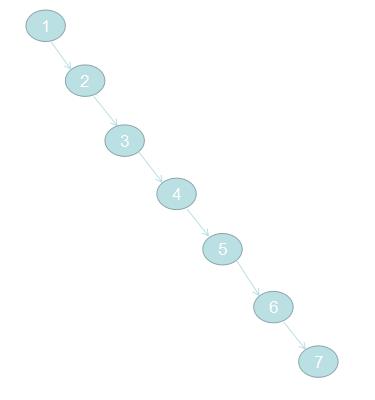
　　后一个数据总是比前一个数据大，那么就会一直在根节点的右节点上。

　　构建最优二叉树的核心就是添加节点的函数，记录当前节点，如果新数据比当前节点小，则让新数据成为左节点。否则成为右节点。

　　代码如下：

function addNode(ele){
    var n = new Node(ele, null, null);
    var Que = [];
    if(this.root == null)
    {
        this.root = n;
    }
    else {
            var curr = this.root;
            var parent;
             while(true)
             {
                 parent = curr;
                 if(ele<curr.element)
                 {
                     curr = curr.left;
                     if( curr == null)
                     {
                     parent.left = n;
                     break;
                     }
                 }
                 else{
                     curr = curr.right;
                     if(curr == null)
                     {
                         parent.right = n;
                         break;
                     }
                 }
             }

         }

    }

}
 

　　可是目的并不是创建最优二叉树，而是创建1，2，3，4，5，6，7这样的二叉树，那么如何实现呢？

　　思路：用一个队列来存储节点，将根节点放入队列中，如果根节点既有左节点又有右节点，将左右节点放入队列，如果没有左节点，将新数据放在左节点上，如果没有右节点，就将新数据放在右节点上。

　　代码：

function addNode(ele){
    var n = new Node(ele, null, null);
    var Que = [];
    if(this.root == null)
    {
        this.root = n;
    }
    else {
        var curr = this.root;
        Que.push(curr);
    }
    while(Que.length>0)
    {
        curr = Que.shift();
        if(curr.left != null && curr.right != null)
        {
            Que.push(curr.left);
            Que.push(curr.right);
        }
        else if(curr.left == null )
        {
            curr.left = n;
            break;
        }
        else if(curr.right == null)
        {
            curr.right = n;
            break;
        }
    }

}　

　　

　　

 二叉树的遍历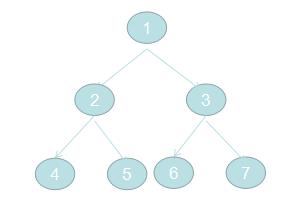

 

　　层次遍历也采用队列思想：

function showLevel(node)
{
    var queue = [];
    var curr;
    if(this.root != null)
    {
        queue.push(this.root)
    }
    while(queue.length>0)
    {
        curr = queue.shift();
        console.info(curr.element)
        if(curr.left != null && curr.right != null)
        {
            queue.push(curr.left);
            queue.push(curr.right);
        }
        else if(curr.left == null )
        {
            continue;
        }
        else if(curr.right == null)
        {
            queue.push(curr.left);
            continue;
        }
    }
}

　执行结果：

　

　　

　　先序遍历:

function showTree(node){
    if(!(node == null))
    {
        node.show();
        showTree(node.left);
        showTree(node.right);
    }
}

　　运行结果：

 

　　

完整代码：

function Node(ele, left, right){
    this.element = ele;
    this.left = left;
    this.right  = right;
    this.show = show;
}
function show(){
    console.log(this.element);
}
function BinaryTree(){
    this.root = null;
    this.addNode = addNode;
    this.showTree = showTree;
    this.showLevel = showLevel;
}

function addNode(ele){
    var n = new Node(ele, null, null);
    var Que = [];
    if(this.root == null)
    {
        this.root = n;
    }
    else {
        var curr = this.root;
        Que.push(curr);
    }
    while(Que.length>0)
    {
        curr = Que.shift();
        if(curr.left != null && curr.right != null)
        {
            Que.push(curr.left);
            Que.push(curr.right);
        }
        else if(curr.left == null )
        {
            curr.left = n;
            break;
        }
        else if(curr.right == null)
        {
            curr.right = n;
            break;
        }
    }

}

function showTree(node){
    if(!(node == null))
    {
        node.show();
        showTree(node.left);
        showTree(node.right);
    }
}

function showLevel(node)
{
    var queue = [];
    var curr;
    if(this.root != null)
    {
        queue.push(this.root)
    }
    while(queue.length>0)
    {
        curr = queue.shift();
        console.info(curr.element)
        if(curr.left != null && curr.right != null)
        {
            queue.push(curr.left);
            queue.push(curr.right);
        }
        else if(curr.left == null )
        {
            continue;
        }
        else if(curr.right == null)
        {
            queue.push(curr.left);
            continue;
        }
    }
}


var Tree = new BinaryTree();
Tree.addNode(1)
Tree.addNode(2)
Tree.addNode(3)
Tree.addNode(4)
Tree.addNode(5)
Tree.addNode(6)
Tree.addNode(7)
showTree(Tree.root)
Tree.showLevel(Tree.root)

　

　　这样，我们就构建了一个二叉树：