最优二叉树

Posted 2022-11-22 wlytctw

一、概述

针对数据结构中的最优二叉树章节，做出笔记，以支持后期的回顾和了解。主要囊括了如下部分：

• 什么是哈弗曼
• 怎么创建最优二叉树
• 哈弗曼编码，用途

二、讲解

1、哈弗曼

定义：
树中带有权值，并且权值最小，路径最短的二叉树，也称为最优二叉树。

如图：
给定权值分别为 4、5、6、7 的A1、B1、C1、D1，可以构成几种或者多中的二叉树。

图a
则该树的带权路径长度（WPL）：4*1+5*3+7*3+6*2 = 52

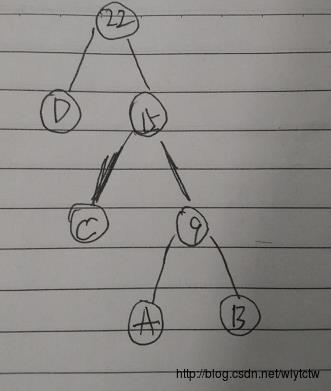
图b
则该树的带权路径长度（WPL）：7*1+6*2+4*3+5*3 = 46
其他的就不在绘制，但是最终发现，每次以最小权值，构建出的二叉树WPL 最小，也就是最小二叉树。（权值越大，离根节点就越近）

2、如何构建最优二叉树

1.从已知结点个数中选择两个权值最小的两个节点，构成二叉树中的左子树、右子数

2.由步骤1,中的左右子树构造一棵新的二叉树，与未使用过的结点或子树组成新的森林。

3.重复步骤1、2，直到森林中构成一棵二叉树为止，
该步骤论述生成的二叉树如图b。

3、哈弗曼编码

可以用作密文编码
若有英文字母构成的密码是：“ACBCCACBCCDCBC”，其中A，B，C，D，分别用二进制码00，01，10，11，分别代替，则译出的二进制密码是“0010011010001001101011100110”，共28位。当然希望代码短，消除冗余度，而且唯一。为了解决这个问题，我们可以使用二叉树来是实现。

首先我们将二叉树的左右分支分别定义为0、1。已知A、B、C、D所代表的权值分别为4、5、6、7，则构造的哈弗曼书为：

字母编码：A(110)，B(111)，C(10)，D(0)

我们需要说明的是哈弗曼并没有指定和规则说左右分支必须为0、1 的规则，所以我们可以指定左右分支为1、0，这样就是不同的字母编码。
字母编码：A(001)，B(000)，C(01)，D(1).

综述：实现频度越高的字符，编码越短，而出现频度越低的字符，编码越长，这是合理的。