数学实验 MATLAB？

Posted 2023-05-12

如图第二题

1、什么是美赛

美国大学生数学建模竞赛（MCM/ICM）由美国数学及其应用联合会主办，是唯一的国际性数学建模竞赛，也是世界范围内最具影响力的数学建模竞赛，着重强调研究和解决方案的原创性、团队合作、交流及结果的合理性，体现了参赛选手研究问题、解决方案的能力及团队合作精神，为现今各类数学建模竞赛之鼻祖。赛题内容涉及经济、管理、环境、资源、生态、医学、安全等众多领域。

2、关于美赛

美国大学生数学建模竞赛目前分为两种类型MCM（Mathematical Contest In Modeling）和ICM（Interdisciplinary Contest In Modeling)，两种类型竞赛采用统一标准进行，竞赛题目出后，参赛队伍通过美赛官网进行选题，一共分为6种题型：

每个团队由1-3名同一所学校/机构中全日制或非全日制注册的本科生学生组成。在四天时间内，就指定的问题完成从建立模型、求解、验证到论文撰写的全部工作。

3、只要努努力，你就可以获奖

比赛奖项一般设置七项，Finalist 进入特等奖角逐未得到特等奖;且Unsuccessful Participant 和Disqualified 不计入统计。

67.50%+15.35%+7.09%+0.17%+0.14%=90.25%

4、2022年美赛关键时间点

报名截止时间 美国东部时间2022年2月17日 15:00之前（星期四） 北京时间2022年2月18日 凌晨4:00之前（星期五）

比赛开始时间 美国东部时间2022年2月17日 17:00（星期四） 北京时间2022年2月18日 上午6:00（星期五）

比赛截止时间 美国东部时间2022年2月21日 20:00（星期一） 北京时间2022年2月22日 上午9:00（星期二）

提交方案截止时间 美国东部时间2022年2月21日 21:00（星期一） 北京时间2022年2月22日 上午10:00（星期二）

比赛结果公布时间 美国东部时间2022年5月20日之前发布

2022年美赛（MCM/ICM）辅助报名

识别二维码立即报名

辅助报名优势

通过辅助报名过程简单，直接在线报名组队，使用微信/支付宝即可缴费，无须VISA等国外银行卡，很大程度地方便了学生的报名。了解详情请识别上方二维码！

欢迎同学们加入QQ交流群

5、参加美赛能获得什么？

1. 锻炼和增强数学应用和科研创新能力；

2. 提升英语水平（最终参赛论文全部以英文形式提交）；

3. 保研留学直通车（美赛奖项价值颇高，在申请奖学金、保研和出国留学时具有很大优势）。

6、美赛准备小tips

为了帮助数学建模初学者快速学习数学建模，掌握数学建模基本知识，极值学院邀请数模名师肖老师、周老师、清华张博士、上交张博士共同开展了“数学建模系统培训课程”课程。

课程内容依托《全国大学生数学建模竞赛指南》书籍，重点讲解数学建模方法的原理和编程实现算法，深入浅出地为参赛者们讲解数学模型、Matlab编程、论文写作方法等各方面数学建模基础知识。

数学建模竞赛是一项综合的技术，不光学习成绩好就能拿到奖项，需要综合应用数学的能力、编程能力、网络搜索方法、论文写作方法、团队配合能力等。

自己看书入门有一定困难，建议在老师的指导下，边学习边练习能达到更好的学习效果。

课程福利

《大学生数学建模竞赛指南》书籍1本

100G 的数模资料大礼包（历年国赛、美赛优秀论文集、软件资料集、教程等）

课程内容

课程大纲

（上下滑动查看全部）

第一章：数学建模竞赛入门

1、数学建模基础
2、数学建模简单模型
养猪致富、体育决策、传染模型、天气预测、衰变测年
3、论文写作排版
全文搭结构、逐条磨细节、档次靠亮点、功力在深美
4、竞赛简介与文献检索
了解赛事概况与评阅，查找文献助推思路

第二章：数学实验操作

5、MATLAB入门——快速掌握matlab基本用法
6、lingo入门——快速掌握lingo基本用法
7、用MATLAB求解一些基本的高数问题
8、用MATLAB求解一些基本的概率论问题
9、用MATLAB进行矩阵运算和解决线性代数类问题
10、MATLAB工具箱——封装好的功能直接调用

第三章：数学模型与算法

11、线性规划
线性规划与整数线性规的分类
12、非线性规划
罚函数法、近似规划法、二次规划和一般非线性规划
13、层次分析法
层次分析法的原理与步骤
14、插值与拟合
不同次方的插值与拟合的MATLAB求解方法
15、时间序列
移动平均法、指数平滑法、自适应滤波法
16、微分方程
微分方程（A题的重点）的基本介绍与经典案例
17、动态规划
基本概念与最短路问题、投资分配问题和背包问题
18、回归与统计
参数估计、显著性检验、置信区间、逐步回归分析
19、经济类问题
五类相关经济问题的处理方法
20、计算机模拟
应用随机数的蒙特卡罗（Monte Carlo）方法及求解实例
21、图论
TSP问题、最短路问题、状态转移、最优树问题、竞赛图
22、排队论
详解排队论的四种重要模型及其求解
23、数据处理类问题
Logistic模型、灰色预测、神经网络、模糊综合评判
24、智能算法
元胞自动机、模拟退火与遗传算法

主讲老师

肖老师

985高校数学建模教练，人称“模教教主”。发表科研论文41篇， 带队获得国际竞赛：特等奖1项,一等奖12项，二等奖11项，获得全国竞赛:全国一等9项，获得研究生数模竞赛全国一等奖2项，二等奖7项。主编教材《大学生数学建模竞赛指南》、《实用数学建模与软件应用》、《基于Matlab和Lingo的数学实验》、《统计计算与软件应用》 等7本书籍。

朱老师

大学数学建模实验室主任，科技论文写作专家。2000年起先后指导学生参加各类大学生数学建模竞赛、节能减排社会实践与科技竞赛、挑战杯科技竞赛等。指导学生发表科技论文600多篇。

周老师

985高校副教授，硕士生导师。作为数学建模教练指导学生参加国际大学生数学建模竞赛获得特等奖一次、特等奖提名两次。

建模狂人

清华大学博士生，曾获得MathorCup 大学生数学建模挑战赛特等奖，美国大学生数学建模竞赛一等奖（两项），“高教社杯”全国大学生数学建模竞赛二等奖（两项），以及其他类型的数学建模竞赛奖项80多项。学校的数学建模竞赛指导和培训骨干成员。

如何报名课程

扫码查看课程详情

咨询课程获取资料

扫码添加老师微信

回复“数模资料”

即可免费领取建模竞赛资料大礼包

2022年美国大学生数学建模竞赛指南

资料一览表

（上下滑动查看全部）

千里之行，始于足下


快来PICK这份美赛指南

参考技术A

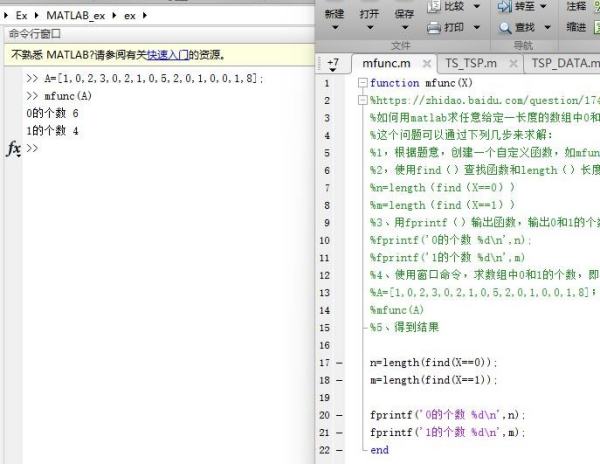
如何用matlab求任意给定一长度的数组中0和1的个数？

这个问题可以通过下列几步来求解：

1，根据题意，创建一个自定义函数，如mfunc(X)

2，使用find（）查找函数和length（）长度函数，来查找0和1。即

n=length（find（X==0））

m=length（find（X==1））

3、用fprintf（）输出函数，输出0和1的个数，即

fprintf('0的个数 %d\\n',n);

fprintf('1的个数 %d\\n',m)

4、使用窗口命令，求数组中0和1的个数，即

A=[1,0,2,3,0,2,1,0,5,2,0,1,0,0,1,8]；

mfunc(A)

5、得到结果

参考技术B

1、什么是美赛

美国大学生数学建模竞赛（MCM/ICM）由美国数学及其应用联合会主办，是唯一的国际性数学建模竞赛，也是世界范围内最具影响力的数学建模竞赛，着重强调研究和解决方案的原创性、团队合作、交流及结果的合理性，体现了参赛选手研究问题、解决方案的能力及团队合作精神，为现今各类数学建模竞赛之鼻祖。赛题内容涉及经济、管理、环境、资源、生态、医学、安全等众多领域。

2、关于美赛

美国大学生数学建模竞赛目前分为两种类型MCM（Mathematical Contest In Modeling）和ICM（Interdisciplinary Contest In Modeling)，两种类型竞赛采用统一标准进行，竞赛题目出后，参赛队伍通过美赛官网进行选题，一共分为6种题型：

每个团队由1-3名同一所学校/机构中全日制或非全日制注册的本科生学生组成。在四天时间内，就指定的问题完成从建立模型、求解、验证到论文撰写的全部工作。

3、只要努努力，你就可以获奖

比赛奖项一般设置七项，Finalist 进入特等奖角逐未得到特等奖;且Unsuccessful Participant 和Disqualified 不计入统计。

67.50%+15.35%+7.09%+0.17%+0.14%=90.25%

4、2022年美赛关键时间点

报名截止时间 美国东部时间2022年2月17日 15:00之前（星期四） 北京时间2022年2月18日 凌晨4:00之前（星期五）

比赛开始时间 美国东部时间2022年2月17日 17:00（星期四） 北京时间2022年2月18日 上午6:00（星期五）

比赛截止时间 美国东部时间2022年2月21日 20:00（星期一） 北京时间2022年2月22日 上午9:00（星期二）

提交方案截止时间 美国东部时间2022年2月21日 21:00（星期一） 北京时间2022年2月22日 上午10:00（星期二）

比赛结果公布时间 美国东部时间2022年5月20日之前发布

2022年美赛（MCM/ICM）辅助报名

识别二维码立即报名

辅助报名优势

通过辅助报名过程简单，直接在线报名组队，使用微信/支付宝即可缴费，无须VISA等国外银行卡，很大程度地方便了学生的报名。了解详情请识别上方二维码！

欢迎同学们加入QQ交流群

5、参加美赛能获得什么？

1. 锻炼和增强数学应用和科研创新能力；

2. 提升英语水平（最终参赛论文全部以英文形式提交）；

3. 保研留学直通车（美赛奖项价值颇高，在申请奖学金、保研和出国留学时具有很大优势）。

6、美赛准备小tips

为了帮助数学建模初学者快速学习数学建模，掌握数学建模基本知识，极值学院邀请数模名师肖老师、周老师、清华张博士、上交张博士共同开展了“数学建模系统培训课程”课程。

课程内容依托《全国大学生数学建模竞赛指南》书籍，重点讲解数学建模方法的原理和编程实现算法，深入浅出地为参赛者们讲解数学模型、Matlab编程、论文写作方法等各方面数学建模基础知识。

数学建模竞赛是一项综合的技术，不光学习成绩好就能拿到奖项，需要综合应用数学的能力、编程能力、网络搜索方法、论文写作方法、团队配合能力等。

自己看书入门有一定困难，建议在老师的指导下，边学习边练习能达到更好的学习效果。

课程福利

《大学生数学建模竞赛指南》书籍1本

100G 的数模资料大礼包（历年国赛、美赛优秀论文集、软件资料集、教程等）

课程内容

课程大纲

（上下滑动查看全部）

第一章：数学建模竞赛入门

1、数学建模基础
2、数学建模简单模型
养猪致富、体育决策、传染模型、天气预测、衰变测年
3、论文写作排版
全文搭结构、逐条磨细节、档次靠亮点、功力在深美
4、竞赛简介与文献检索
了解赛事概况与评阅，查找文献助推思路

第二章：数学实验操作

5、MATLAB入门——快速掌握matlab基本用法
6、lingo入门——快速掌握lingo基本用法
7、用MATLAB求解一些基本的高数问题
8、用MATLAB求解一些基本的概率论问题
9、用MATLAB进行矩阵运算和解决线性代数类问题
10、MATLAB工具箱——封装好的功能直接调用

第三章：数学模型与算法

11、线性规划
线性规划与整数线性规的分类
12、非线性规划
罚函数法、近似规划法、二次规划和一般非线性规划
13、层次分析法
层次分析法的原理与步骤
14、插值与拟合
不同次方的插值与拟合的MATLAB求解方法
15、时间序列
移动平均法、指数平滑法、自适应滤波法
16、微分方程
微分方程（A题的重点）的基本介绍与经典案例
17、动态规划
基本概念与最短路问题、投资分配问题和背包问题
18、回归与统计
参数估计、显著性检验、置信区间、逐步回归分析
19、经济类问题
五类相关经济问题的处理方法
20、计算机模拟
应用随机数的蒙特卡罗（Monte Carlo）方法及求解实例
21、图论
TSP问题、最短路问题、状态转移、最优树问题、竞赛图
22、排队论
详解排队论的四种重要模型及其求解
23、数据处理类问题
Logistic模型、灰色预测、神经网络、模糊综合评判
24、智能算法
元胞自动机、模拟退火与遗传算法

主讲老师

肖老师

985高校数学建模教练，人称“模教教主”。发表科研论文41篇， 带队获得国际竞赛：特等奖1项,一等奖12项，二等奖11项，获得全国竞赛:全国一等9项，获得研究生数模竞赛全国一等奖2项，二等奖7项。主编教材《大学生数学建模竞赛指南》、《实用数学建模与软件应用》、《基于Matlab和Lingo的数学实验》、《统计计算与软件应用》 等7本书籍。

朱老师

大学数学建模实验室主任，科技论文写作专家。2000年起先后指导学生参加各类大学生数学建模竞赛、节能减排社会实践与科技竞赛、挑战杯科技竞赛等。指导学生发表科技论文600多篇。

周老师

985高校副教授，硕士生导师。作为数学建模教练指导学生参加国际大学生数学建模竞赛获得特等奖一次、特等奖提名两次。

建模狂人

清华大学博士生，曾获得MathorCup 大学生数学建模挑战赛特等奖，美国大学生数学建模竞赛一等奖（两项），“高教社杯”全国大学生数学建模竞赛二等奖（两项），以及其他类型的数学建模竞赛奖项80多项。学校的数学建模竞赛指导和培训骨干成员。

如何报名课程

扫码查看课程详情

咨询课程获取资料

扫码添加老师微信

回复“数模资料”

即可免费领取建模竞赛资料大礼包

2022年美国大学生数学建模竞赛指南

资料一览表

（上下滑动查看全部）

千里之行，始于足下


快来PICK这份美赛指南

SOR迭代法实验报告c语言,数学实验“线性方程组的J-迭代,GS-迭代,SOR-迭代解法”实验报告(内含matlab程序代码).doc...

西京学院数学软件实验任务书

课程名称

数学软件实验

班级

数0901

学号

0912020107

姓名

李亚强

实验课题

线性方程组的J-迭代，GS-迭代，SOR-迭代方法。

实验目的

熟悉线性方程组的J-迭代，GS-迭代，SOR-迭代方法。

实验要求

运用Matlab/C/C++/Java/Maple/Mathematica等其中一种语言完成。

实验内容

线性方程组的J-迭代；

线性方程组的GS-迭代；

线性方程组的SOR-迭代。

成绩

教师

实验四实验报告

1、 实验名称：线性方程组的J-迭代，GS-迭代，SOR-迭代。

2、 实验目的：熟悉线性方程组的J-迭代，GS-迭代，SOR-迭代，SSOR-迭代方法，编程实现雅可比方法和高斯-赛德尔方法求解非线性方程组的根，提高matlab编程能力。

3、 实验要求：已知线性方程矩阵，利用迭代思想编程求解线性方程组的解。

4、 实验原理：

1、雅可比迭代法(J-迭代法)：

线性方程组，可以转变为：

迭代公式

其中，称为求解的雅可比迭代法的迭代矩阵。以下给出雅可比迭代的分量计算公式，令，由雅可比迭代公式有

，既有，于是，解的雅可比迭代法的计算公式为

2、 高斯-赛德尔迭代法(GS-迭代法)：

GS-迭代法可以看作是雅可比迭代法的一种改进，给出了迭代公式：

其余部分与雅克比迭代类似。

3、 逐次超松弛迭代法(SOR-迭代法)：

选取矩阵A的下三角矩阵分量并赋予参数w，将之作为分裂矩阵M，，其中，w>0，为可选择的松弛因子，又(1)公式构造一个迭代法，其迭代矩阵为从而得到解的逐次超松弛迭代法。

其中：

由此，解的SOR-迭代法的计算公式为

(2)

观察(2)式，可得结论：

(1) 、当w=1时，SOR-迭代法为J-迭代法。

(2) 、当w>1时，称为超松弛迭代法，当w<1时，称为低松弛迭代法。

5、 实验内容：

%1.J-迭代

function x1=jacobi(A,b,y);

m=input('请输入迭代次数m:');

eps=input('请输入精度eps:');

D=diag(diag(A));

L=triu(A)-A;

U=tril(A)-A;

M=D\\(L+U);

g=D\\b;

a=1;

k=0;

while a>eps

x2=M*x1+g;

a=norm(x2-x1,inf);

x1=x2;

k=k+1;

end

%输出方程组的近似解、精确值及误差

disp('近似解：');

disp(x1);

x2=x1-y;

a=norm(x2,inf);

fprintf('误差：%.6f;迭代次数：%d\\n',a,k);

%2.GS-迭代

function x1=G_S(A,b,y)

n=100;

m=input('请输入迭代次数m:');

eps=input('请输入精度eps:');

D=diag(diag(A));

L=triu(A)-A;

U=tril(A)-A;

%生成矩阵M,向量g

M=(D-L)\\U;

g=(D-L)\\b;

%迭代首项

x1=eye(n-1,1);

x2=eye(n-1,1);

for i=1:n-1

x1(i)=1;

x2(i)=0;

end

a=1;

k=0;

while a>eps

x2=M*x1+g;

a=norm(x2-x1,inf);

x1=x2;

k=k+1;

end

%输出方程组的近似解、精确值及误差

disp('近似解：')；

x2=x1-y;

a=norm(x2,inf);

fprintf('误差：%.4f;迭代次数：%d\\n',a,k);

%3.SOR-迭代

function a=p(A)

[n,n]=size(A);

x=eig(A);

a=0;

for i=1:n

b=abs(x(i));

if b>a

a=x(i);

end

end

a=abs(a);

function x1=SOR(A,b,y) %y为精确解

%超松弛迭代

D=diag(diag(A));

L=triu(A)-A;

U=tril(A)-A;

%求最佳松弛因子w

M=D\\(L+U);

w=p(M);

w=2/(1+sqrt(1-w^2));

if w<0||w>2

disp('迭代不收敛');

return;

end

%生成矩阵M,向量g

M=(D-w*L)\\((1-w)*D+w*U);

g=(D-w*L)\\b*w;

%进行迭代

w=1;

k=0;

%x1=eye(n,1);

while w>1e-6

x2=M*x1+g;

w=norm(x2-x1,inf);

x1=x2;

k=k+1;

end

%输出方程组的近似解、精确值及误差

disp('近似解：');

disp(x1);

x2=x1-y;

w=norm(x2,inf);

disp('误差:');

disp(w);

disp('迭代次数：');

disp(k);

6、 实验结果：

A=[5 2 0;6 4 1;1 2 5];b=[10 18 -14]';

X1= G_S (A,b,[0 0 0]')

X1 =

-0.8750

7.1874

-5.5000

- 9 -

展开阅读全文