运筹学的图书目录

Posted 2023-05-12

参考技术A

第1章 绪论
1.1 运筹学发展简史
1.2 运筹学的内容及特点
1.3 运筹学在管理领域
的应用
1.4 运筹学的展望
第2章 线性规划及单纯
形法
2.1 线性规划的概念及
其建模
2.2 图解法
2.3 线性规划解的概
念、性质
2.4 单纯形法
2.5 线性规划应用举例
2.6 上机指导——使用
QSB软件求解线性规划
第3章 对偶理论与灵敏度
分析
3.1 线性规划的对偶问题
3.2 线性规划的对偶理论
3.3 影子价格
3.4 对偶单纯形法
3.5 灵敏度分析
第4章 运输问题
4.1 运输问题概念及模型
4.2 表上作业法求解运
输问题
4.3 产销不平衡的运输
问题
4.4 运输问题的应用举例
第5章 整数规划
5.1 整数规划问题的模
型及解的特点
5.2 0-1规划
5.3 指派问题
5.4 上机指导——使用
QSB软件求解整数规划
第6章 动态规划
6.1 多阶段决策过程的最
优化
6.2 动态规划的基本概
念和基本原理
6.3 动态规划模型的建
立和求解
6.4 动态规划在经济管
理中的应用
6.5 上机指导——使用
QSB软件求解动态规划
问题
第7章 对策论
7.1 对策论的基本概念
7.2 矩阵对策的基本理论
7.3 矩阵对策的求解
7.4 矩阵对策的应用
第8章 决策分析
8.1 决策的分类与过程
8.2 不确定型决策
8.3 风险型决策
8.4 效用理论在决策中的
应用
第9章 存贮论
9.1 存贮论的基本概念
9.2 重复周期存贮模型
9.3 单周期存贮模型
第10章 图与网络分析
10.1 图的基本概念与基本
定理
10.2 树
10.3 最短路问题
10.4 最大流问题
10.5 最小费用最大流问题
10.6 网络计划
10.7 上机指导——使用
QSB软件求解最小树和最短路等问题

运筹学笔记 网络计划

文章目录

• • 一. 网络图
  • 二. 时间参数的计算
  • • 1. 工序的作业时间 T( i, j )的确定
    • 2. 事项的时间参数（事项最早时间和最迟时间）
    • 3. 工序的时间参数（工序最早开始时间、最早结束时间、最迟开工时间、最迟完工时间）
    • 4. 时差（工序的总时差、单时差）
    • 5. 关键路线
  • 三. 网络优化

用网络分析的方法编制的计划称为网络计划。它是五十年代末发展起来的一种编制大型工程进度计划的有效方法。
1956年，美国杜邦公司在制定企业不同业务部门的系统规划时，制定了第一套网络计划。这种计划借助于网络表示各项工作与所需要的时间，以计划时及计划执行过程中的关键路线。

网络计划技术的基本原理：从需要管理的任务的总进度着眼，以任务中各工作做需要的工时为时间因素，按照工作的先后顺序和相互关系作出网络图，以反映任务全貌，实现管理过程的模型化。然后进行时间参数计算，找出计划中的关键工作和关键路线，对任务的各项工作所需的人、财、物通过改善网络计划作出合理安排，得到最优方案并付诸实施。

要解决的问题
1）完成整个项目所需的时间？
2）每一特定作业的开工和完工之进度表是什么？
3）哪些是“关键作业”必须严格按时间表完成？
4）哪些是“非关键作业”？可以拖延的时间是多少？
5）成本如何与时间进行交换？

编制整个网络计划包括： 绘制网络图，计算时间参数，确定关键路线以及网络优化等环节。
下面分别讨论这些内容。

一. 网络图

区别于前面讲的网络图，在此网络图有一些自身的特点和要求，需要专门叙述。

一. 网络图的一些基本概念
1 . 网络图——网络图是由节点、弧及权所构成的有向图，即赋权有向图。
2 . 节点表示一个事项，它是一个或若干个工序的开始或结束，是相邻工序在时间上的分界点。节点用圆圈和里面的数字表示，数字表示节点的编号，如①、②等。
3 . 弧表示一个工序，工序是指为了完成工程项目，在工艺技术 和组织管理上相对独立的工作和活动。一项工程由若干个工序组成。工序需要一定的人力、物力等资源和时间。弧用带箭头的线表示。
4 . 权表示为完成某个工序所需要的时间或资源等数据，通常标注在线的上面或下面。
如：某工序a可以表示为：

其中i为节点，表示工序a开始， j为节点，表示工序a的结束，5表示完成本工序所需的时间。
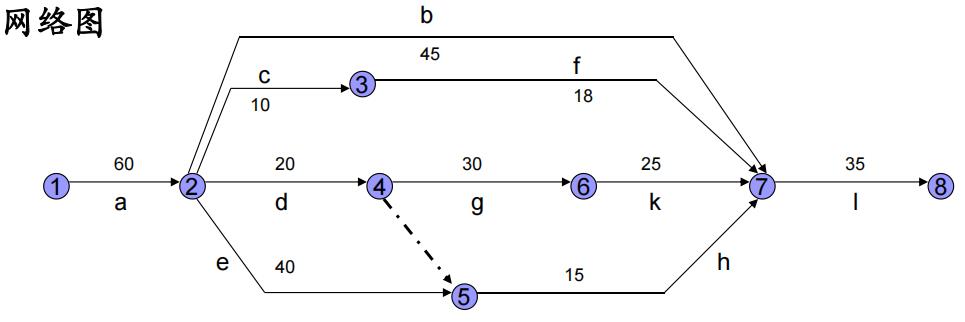
在如：某项新产品投产前全部准备工作，各工序与所需时间以及它们之间的相互关系如下表所示。要求编制该项工程的网络计划。

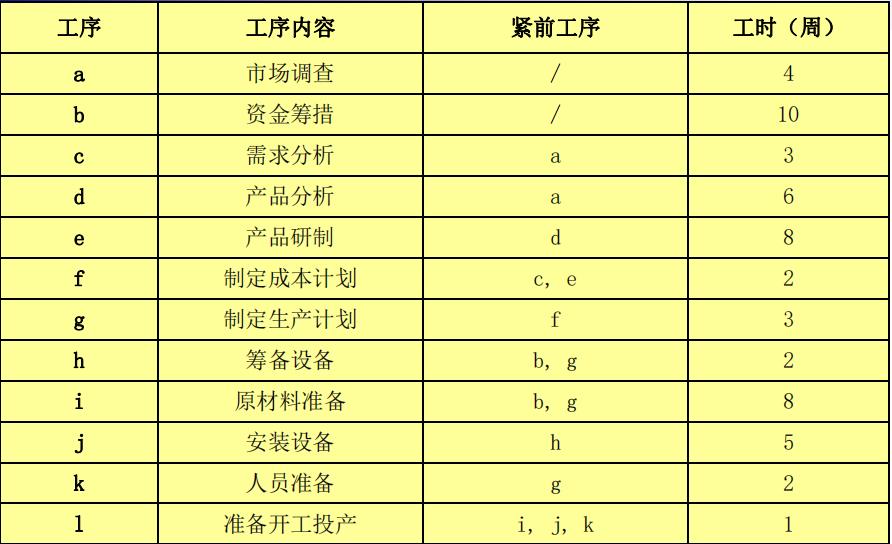
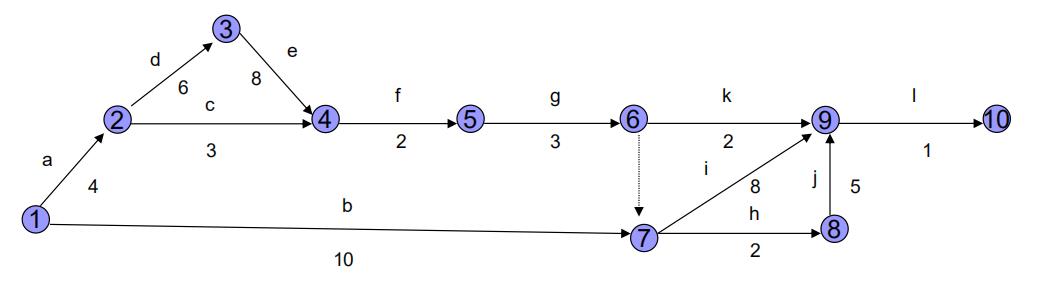在上图中，有向线a, b,…,l分别代表12个工序，有向线下面的数字表示为完出该个工序所需要的时间（天数）。
节点①、②、… 、⑩分别表示某一或某些工序的开始和结束。
如②表示a工序的结束和c、d等工序的开始，即a工序结束后，后2个工序才能开始。

二. 建立网络图的准则和注意事项
为正确反映工程中各个工序的相互关系，在绘制网络图时，应遵循以下规则：
1 . 方向、时序与节点编号
网络图是有向图，按照工艺流程的顺序，规定工序从左向右 排列，再给节点统一编号，节点由小到大编号。
对任一工序 <i, j> 来讲，要求 j>i。始点编号可以从1开始。为 了便于修改编号及调整计划，编号可以不连续，即可以在编号过程中，留出一些编号。 始点编号可以从1开始，图中最大的编号n表示计划结束事项。
2. 始点和终点网络图中只能有一个始点（总起点事项）和终点（总终点事项）
3. 网络图不能有缺口和回路
在网络图中，除始点、终点外，其它各个节点的前后都应有弧连接，即图中不能有缺口，应使网络图从始点经任何路线都可以到达终点。否则，将使某些工序失去与其紧后（或紧前） 工序应有的联系。 也不能有回路，否则将使组成回路的工序永远不能结束，工程永远不能完工。
4. 正确表示工作之间的前行、后继关系
如4道工序a, b, c, d 的关系为：c必须在a, b均完成后才能开工，而 d只要在b 完工后即可开工。若将上述关系画成如下图：

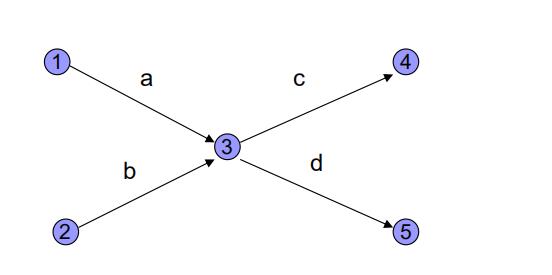
则该图是错误的，因为本来与 a 工作无关的工作 d 被错误地表示为必须在 a 完成后才能开工。
5. 相邻的2个节点之间只能有一条弧
即一个工序用确定的2个相关事项表示，某2个相邻节点只能是一个工序的相关事项。
在计算机上计算各个节点和各个工序的时间参数时，相关事项的2个节点只能表示一道工序，否则将造成逻辑上的混乱。
6. 虚工序的应用
如前面不符合规则的图等，可以用添加虚工作的方法改画。
虚工序：只表示相邻工作之间的逻辑关系，不占用时间和不消耗人力资金等的虚设的工作。可用虚箭线表示……>。
如：
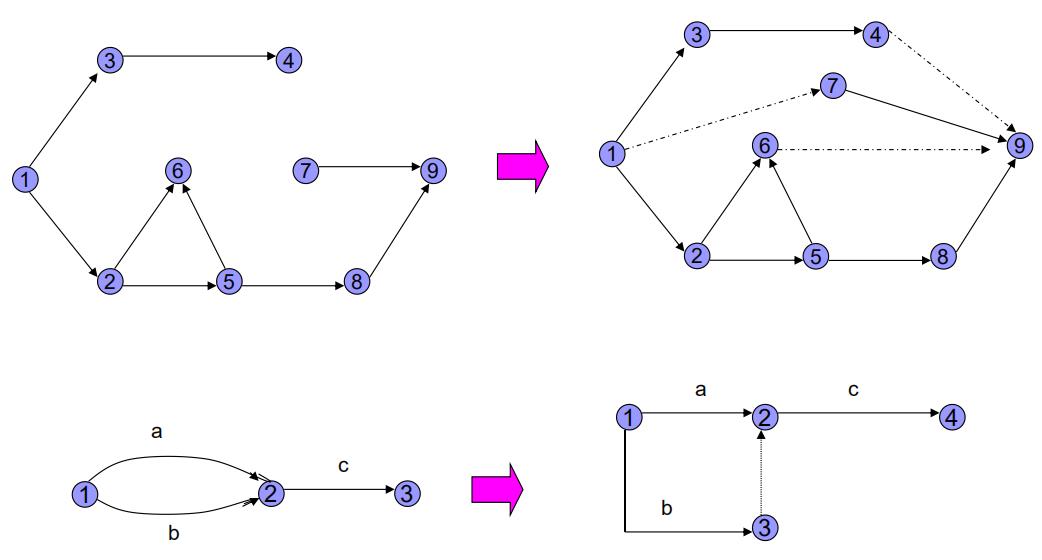如果a, b, c, d的工序关系是：c必须在a、b均完成后才能开工， 而d只要在b完成后即可开工。
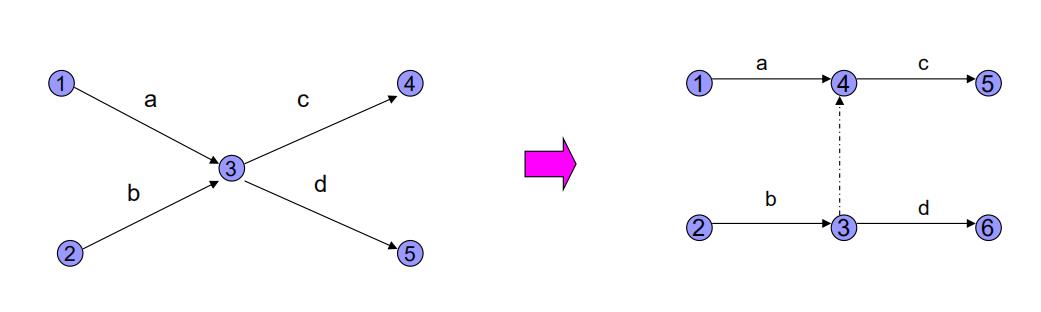其中③→④是一个虚工序，只表示③、④两节点的衔接关系， 不需要人力、物力等资源和时间。

虚工序可以用于正确表示平行与交叉作业。
一道工作分为几道工作同时进行，成为平行工作。
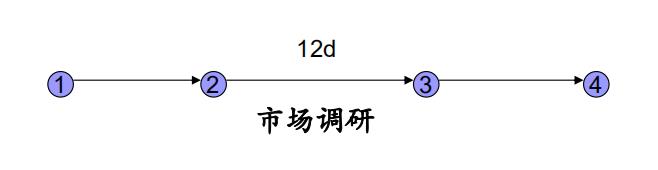
如：下图中市场调研 2…>3 需12天。

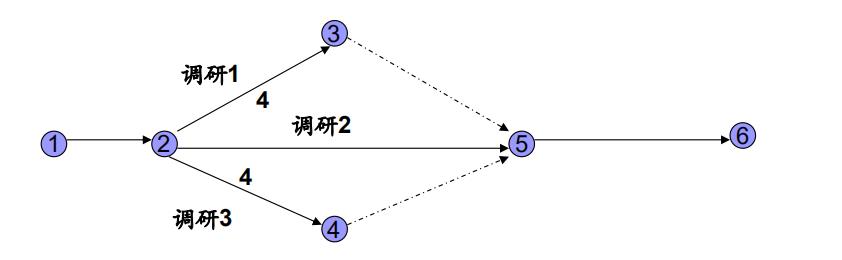
如增加人力分为三组同时进行，则可画为图：
两件或两件以上的工作交叉进行，称为交叉工作。
如工作A与工作B分别为挖沟和埋管子，那么它们的关系可以是挖一段埋一段，不必等沟全部挖好再埋。
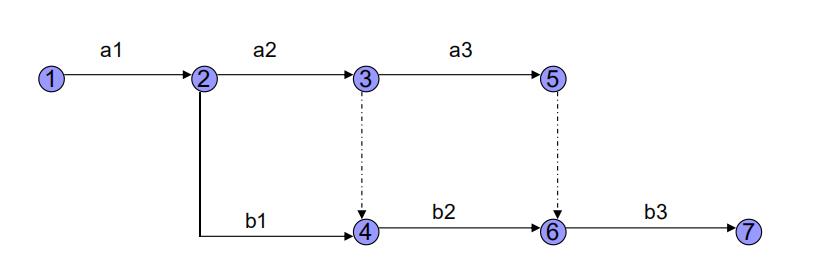
此时可用交叉工作来表示，如把这两件工作各分为三段， A=a1+a2+a3，B=b1+b2+b3，则可用下图表示为：

计算网络图中有关的时间参数，主要的目的是找出关键路线， 为网络计划的优化、调整和执行提供明确的时间概念。

二. 时间参数的计算

计算网络图中有关的时间参数，主要的目的是找出关键路线， 为网络计划的优化、调整和执行提供明确的时间概念。
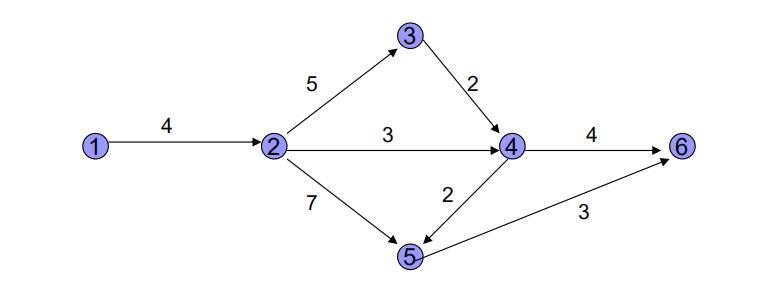可观察网络图中从节点1到节点6的所有通路，分别计算各路线所持续的时间。
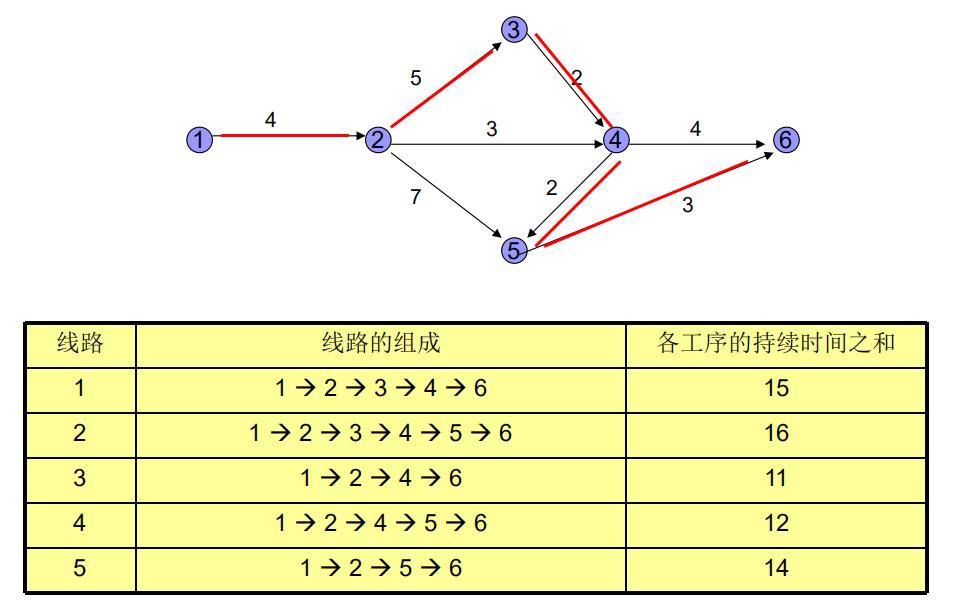5条线路中，其中完成各个工序持续时间最长的线路称为关键路线，或称主要矛盾线。上图第2条线路为关键路线。

完成各个工序持续时间最长的线路称为关键路线，即关键路线为网络图中需时最长的路线。关键路线上的工序称为关键工序。
要想使任务提前完工，就要在关键路线上想办法。
为了编制网络计划和找出关键路线，要计算网络图中各个事项及各个工序的有关时间，称这些有关时间为网络时间。

网络图的时间参数包括工序所需时间、事项最早、最迟的时间，工序的最早、最迟时间及时差等，下面分别叙述：

1. 工序的作业时间 T( i, j )的确定

为完成工序（i，j）所需要的时间称为该工序的作业时间， 可记为T( i, j)。 该参数的计算是一项基础工作，关系到网络计划是否能得到正确实施。
工序的作业时间有以下两种确定方法：
（a）一点时间（单时）估计法
在确定时间时，每项工作只估计或规定一个确定的持续时间值的方法。一般由工作的工作量，劳动定额资料以及投入人力的多少等，计算各工作的持续时间。

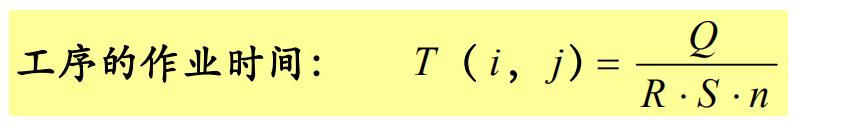
Q：工序的工作量。以时间单位表示，如小时，或以体积、质量、 长度等单位表示；
R：可投入人力和设备的数量；
S：每人或每台设备每工作班能完成的工作量；
n：每天正常工作班数。

（b) 三点时间估计法
在不具备有关工作的持续时间的历史资料时，在较难估计出工作持续时间时，可对工作进行估计三种时间值，然后计算其平均值。这三种时间值是：
乐观时间 （a）——最快可能完成时间，即在顺利情况下，完成 工序所需的最小时间。
最可能完成的时间（m）——在正常条件下，完成工作所需要的时间。
悲观时间（b）——在不顺利条件下，完成工作所需要的时间。
完成工序所需的上述3种时间都具有一定的概率。根据经验，这些时间的概率分布可以认为近似于正态分布。
一般情况下，通过专家估计法，给出三时估计的数据。 可以认为工作进行时出现最顺利和最不顺利的情况比较少， 较多是出现正常的情况。按平均意义可用以下公式计算工作持续时间值：
完成工序所需要的上述三种时间都具有一定的概率。根据经验，这些时间的概率分布可以认为近似于正态分布，

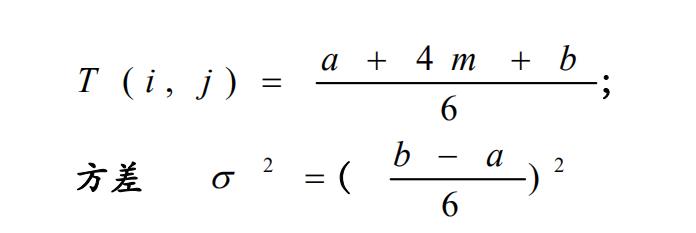
例如，已知某项工程，各关键工序的平均作业时间与方差如下表所示。试求完成该项工序的周期及完工时间为60天的概率。

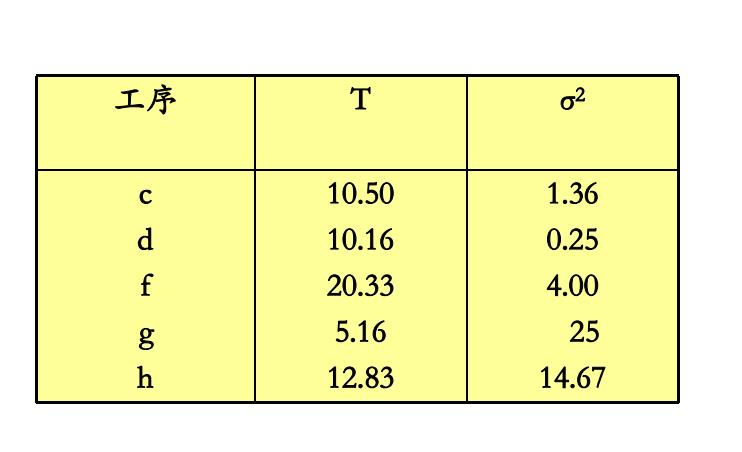
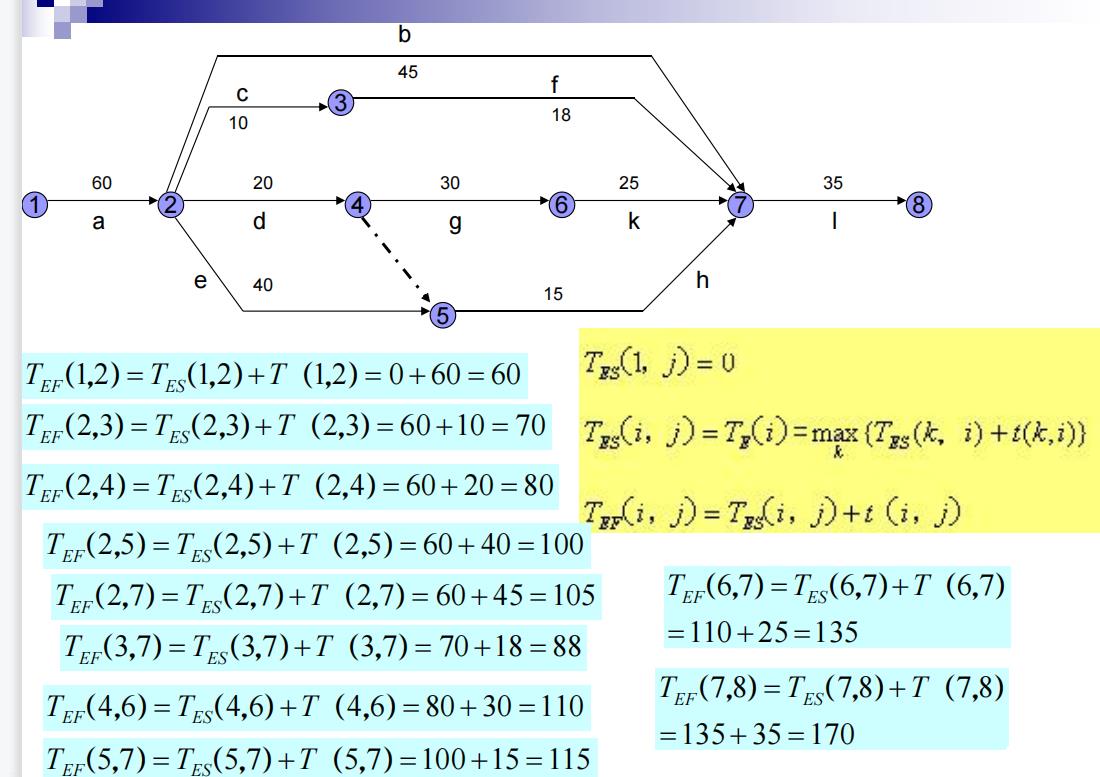
2. 事项的时间参数（事项最早时间和最迟时间）

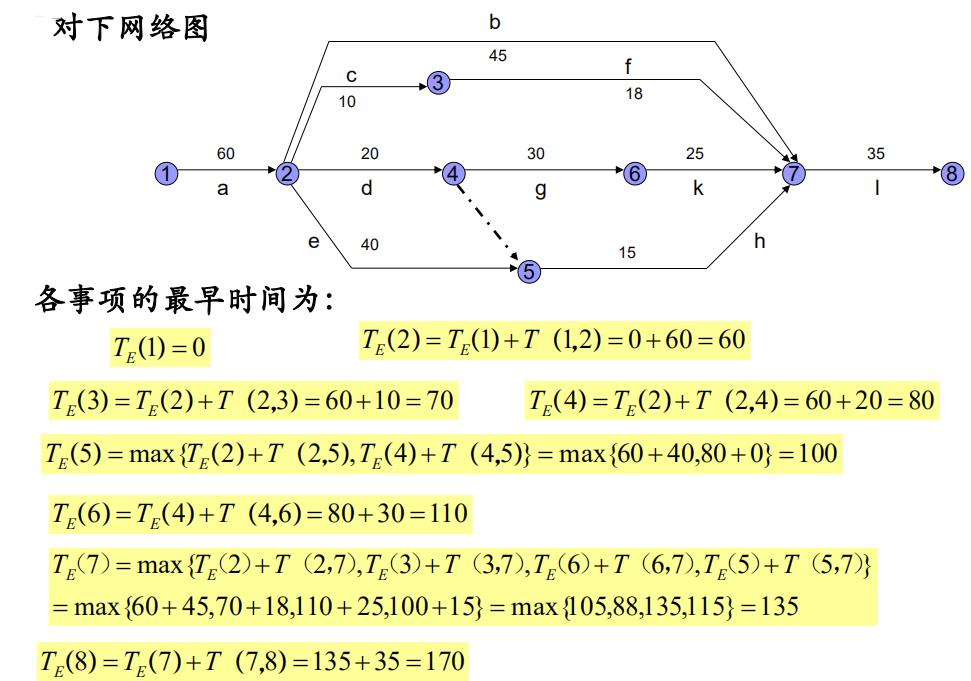
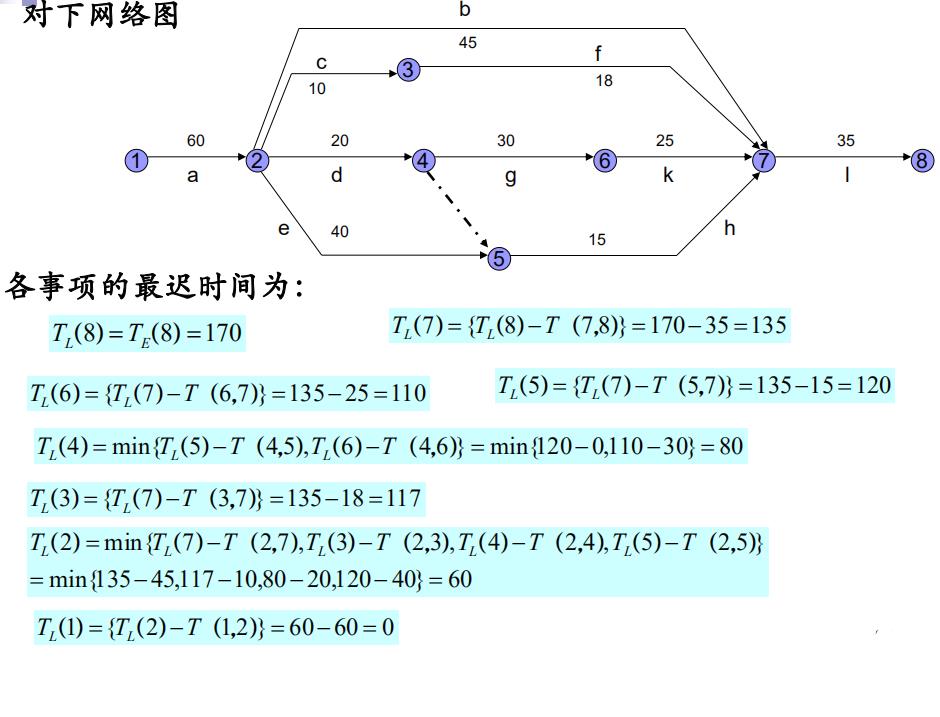
3. 工序的时间参数（工序最早开始时间、最早结束时间、最迟开工时间、最迟完工时间）

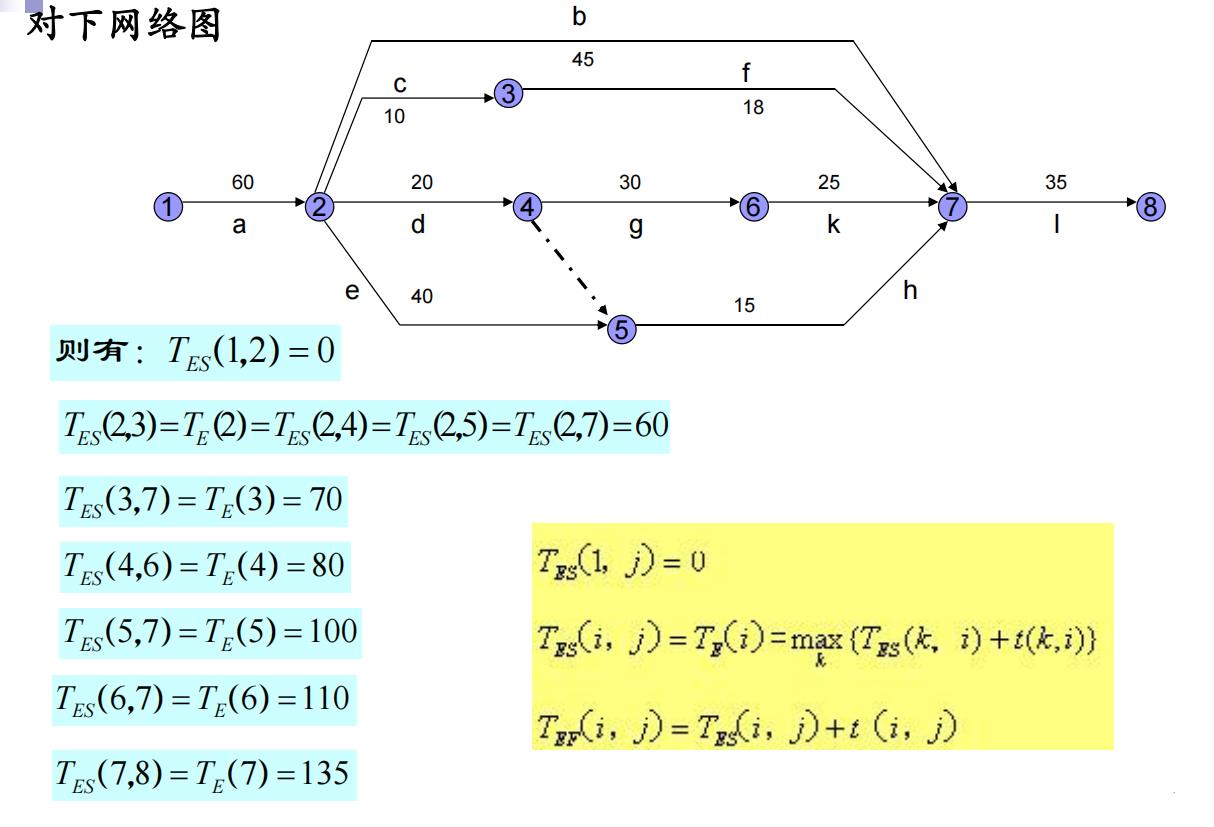
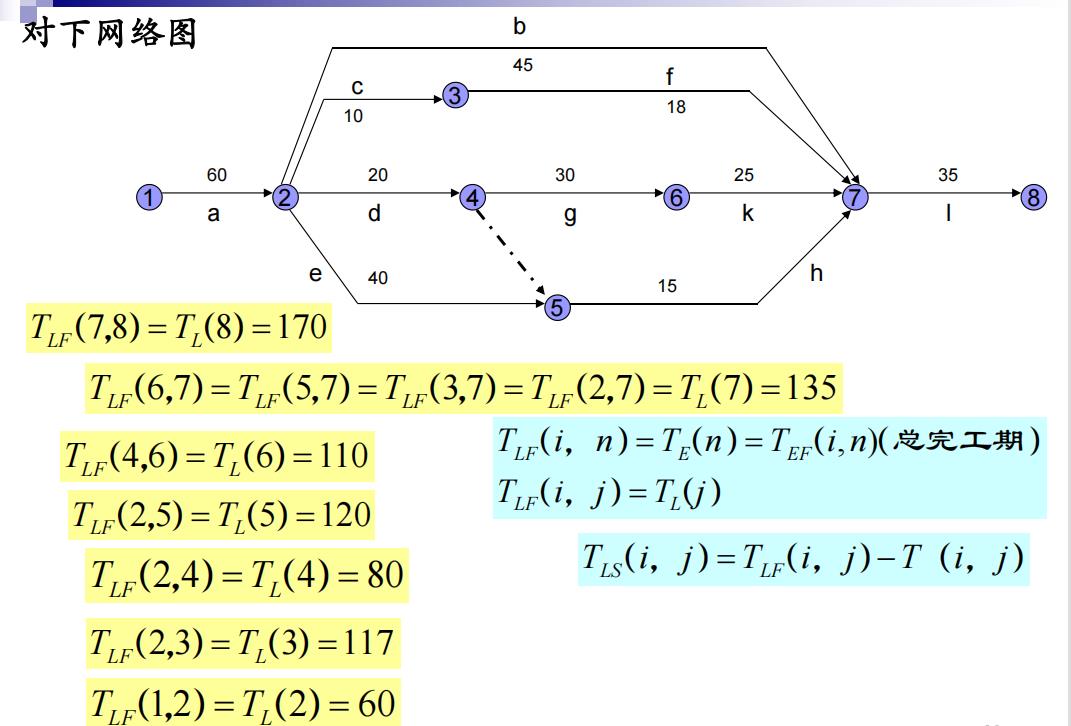
4. 时差（工序的总时差、单时差）

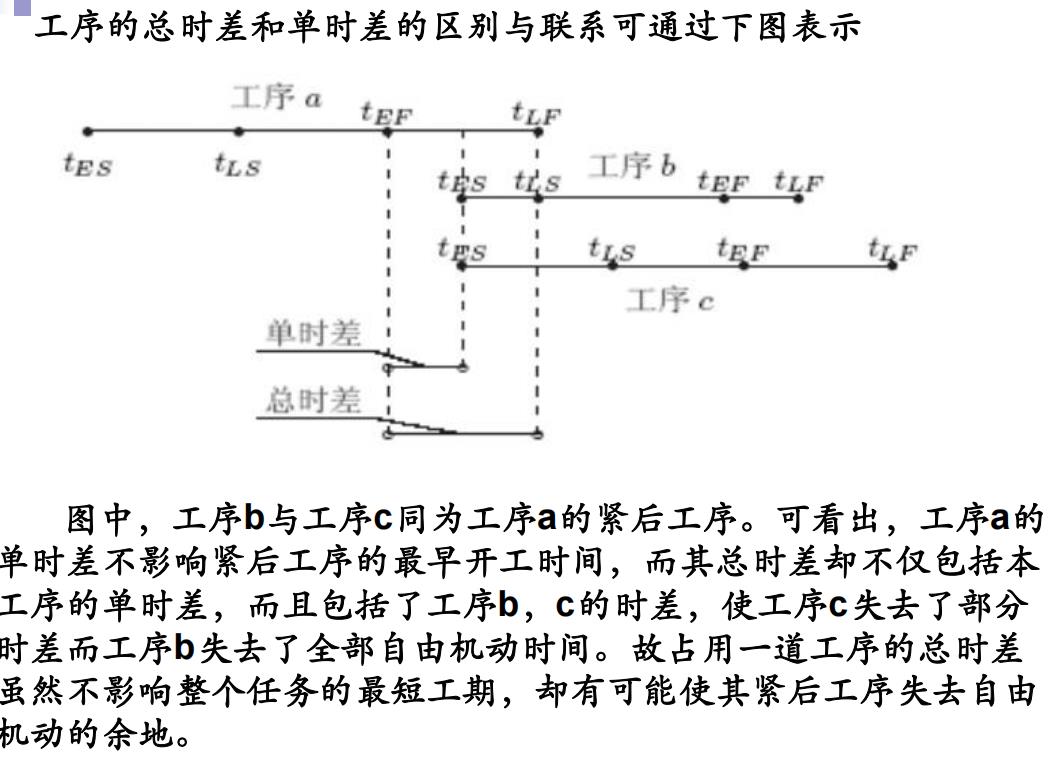
5. 关键路线

网络图中从最初事项——>最终事项的所有不同路线中，作 业总时间延续最长的一条路线称为：关键路线。
在关键路线上，所有工序（i, j）的总时差R（i, j）= 0.
关键路线的意义：
1 . 此条路线的持续时间决定了完成全盘计划所需的最少时间；
2 . 关键路线上的各项作业对影响计划进度起关键作用，是整个工程的薄弱环节，也是需要领导重点抓和安排比较充裕的人力、物力以保证按期完工的关键部位。

在一个PERT网络图中，有时关键路线可能不止一条。此外除关键路线外，还有持续时间十分接近关键路线，被称为次关键路线的一些路线，它也是各线领导指挥人员应该注意抓的环节。因为一旦采取措施缩短了关键路线上作业的完成时间后，那些次关键路线有可能矛盾突出，转变成关键路线。

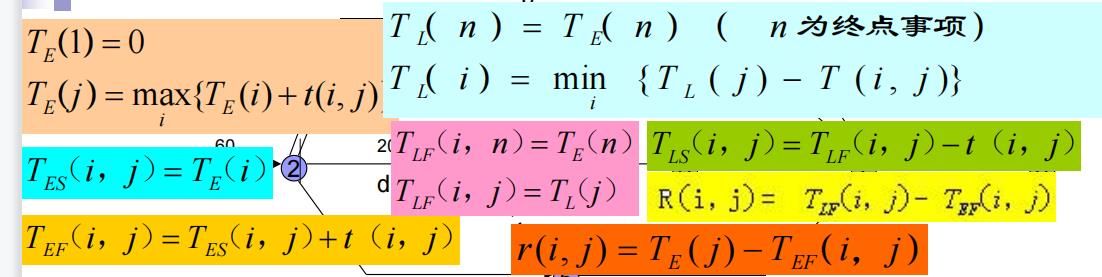
三. 网络优化

绘制网络图、计算网络时间和确定关键路线，得到一个初始的计划方案。
网络优化： 从工期、成本、资源等方面对初步方案做进一步的改善和调整，以求得最佳效果（如缩短工期等）称之。
调整、改善时，需要根据计划的要求，综合地考虑进度，资源利用和降低费用等目标，即进行网络优化，确定最优的计划方案。

目前尚未有能全面反映工期、成本、资源的综合数学模型，因此，网络优化问题是根据实际情况分为时间优化、时间—资源优化和时间—费用优化。
1 . 时间优化(工期优化）
根据对计划进度的要求，缩短工程完工时间。
可以采取的措施有：
• 采取技术措施，提高工效，如把串联工序改为平行或交叉工序，缩短关键工序的作业时间；
• 采取组织措施，充分利用非关键工序的时差，减少这些作业的人力、资源用于关键工序，缩短关键工序的作业时间。

2 . 资源优化
在编制网络计划安排工程进度的同时，就要考虑尽量合理地利用现有资源，并缩短工程周期。
但是，由于一项工程所包含的工序繁多，涉及到的资源利用情况比较复杂，往往不可能在编制网络计划时，一次把进度和资源利用都能够作出统筹合理的安排，常常是需要进行几次综合平衡之后，才能得到在时间进度及资源利用等方面都比较合理的计划方案。

具体的要求和做法是：
(1) 优先安排关键工序所需要的资源；
(2) 利用非关键路线的总时差，错开各工序的开始时间，拉平资源需要量的高峰；
(3) 综合考虑资源和时间，必要时，可适当地推迟工程完工时间。 在优化时，通常将计划的各主要资源需要量按日程排出，再按以上方法，使各主要资源的日负荷相对平衡。

下面举一个拉平资源需要量高峰的实例：
例如：对前已经举的例子，其工程的网络图如下：
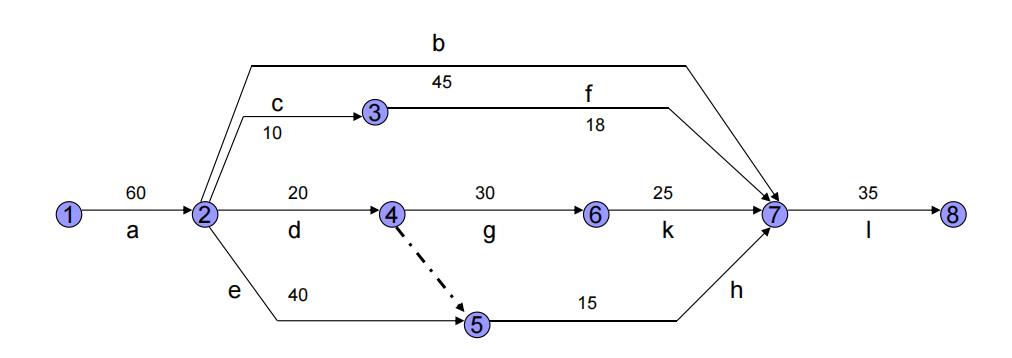现只考虑其中从第2事项到第7事项环节，其网络图可简化如下：
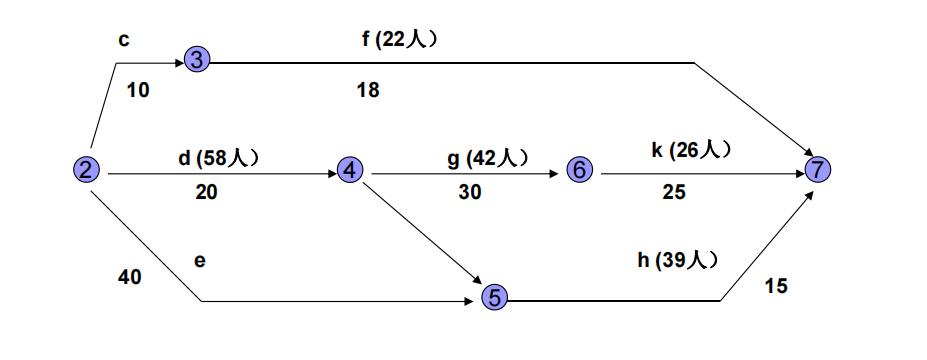若完成工序d, f, g, h, k的机械加工工人数有限制时，并已知现有机械加工工人数为65人，并假设这些工人可以完成上述5个工序中的任何一个工序。

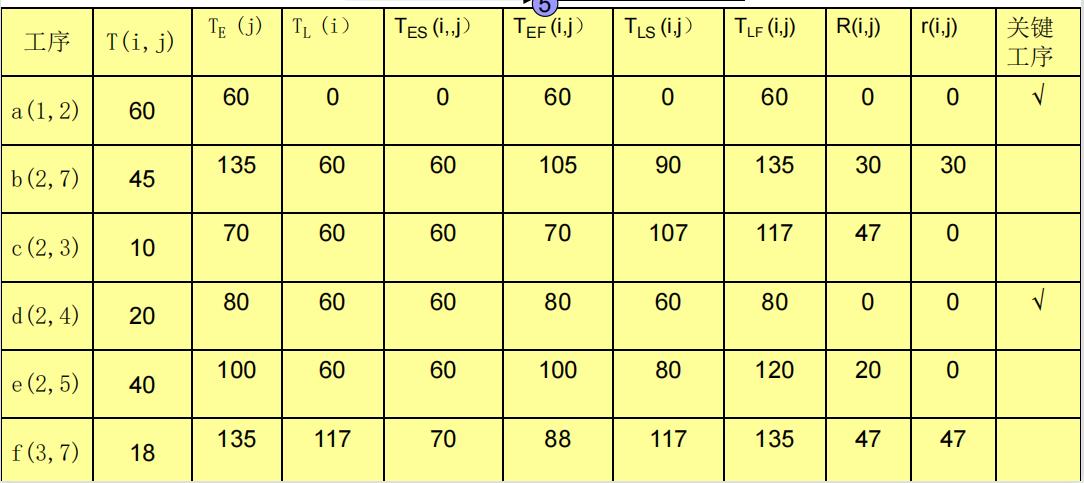
各工序所需要的工人数及上述工序的总时差如下表所示：

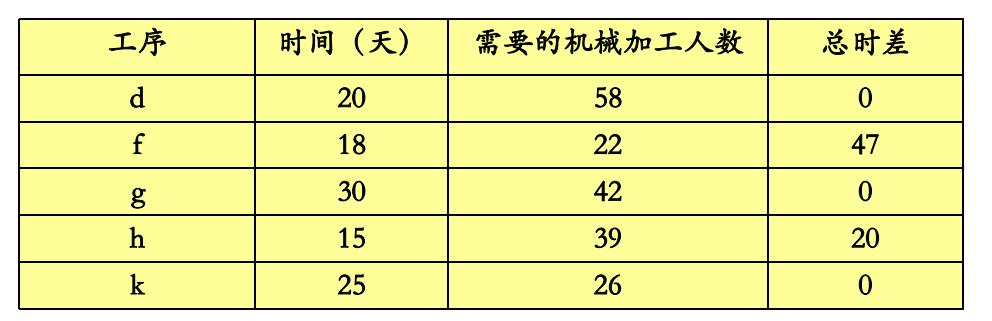
但现有机械加工工人数为65人。
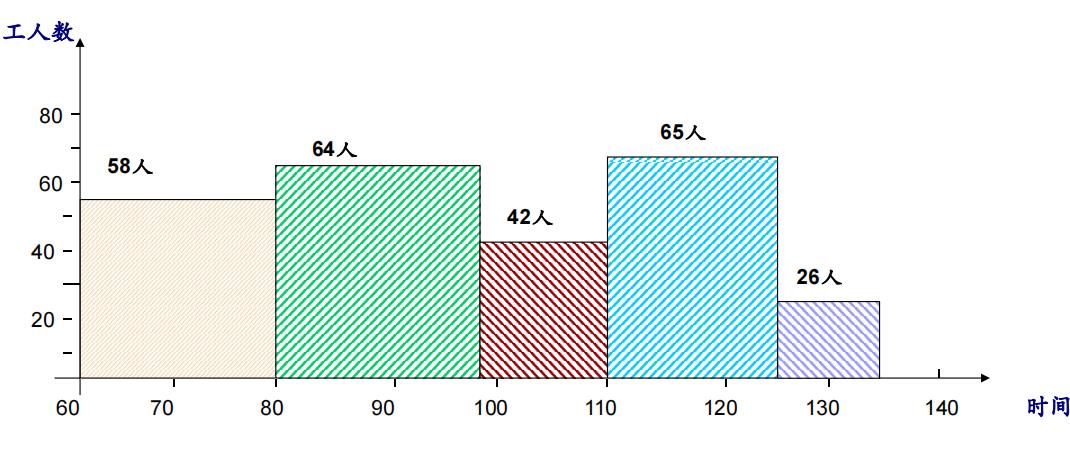
若上述各工序均按最早开始时间安排时，在完成从事项②到事项⑦中各关键工序的75天（=170 - 60 - 35）中，所需要的机械加工工人数如下图所示。


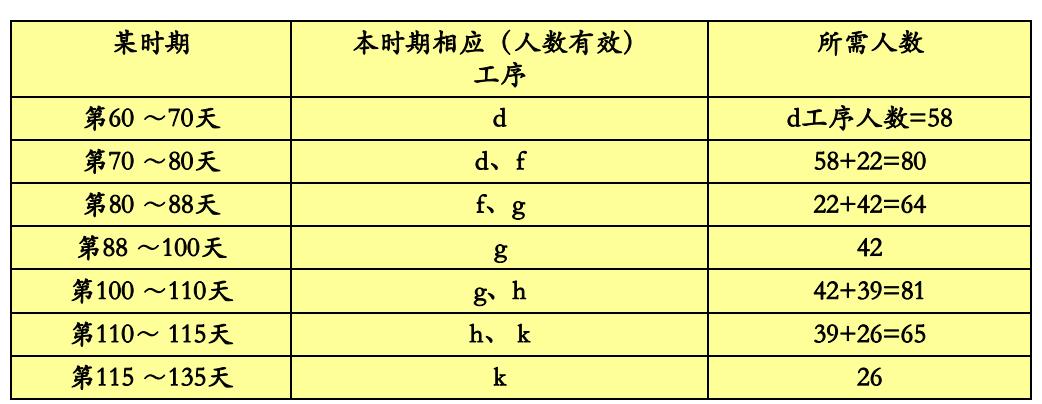
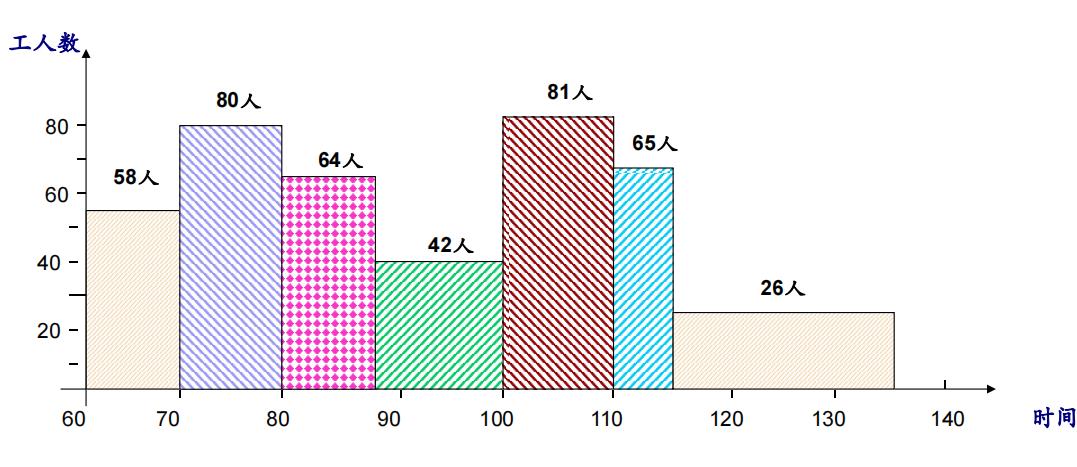
显然，上资源负荷图中的资源负荷是不均匀的，其中有两段时间所需要的工人数都超过了现有工人人数。还有两段时间的工人数远远少于现有工人人数，这种安排是不妥当的。

若各工序都按最迟开始时间安排时，则从第120～135天期间内，需要的机械加工工人数为87（=f、 h、 k工序所需人数=22+26+39）人，也超过了现有的工人数。

下面可以利用非关键工序的总时差，进行调整。
如利用非关键工序f、 h的总时差，由前面计算可知，工序f和h的总时差分别为：R(3,7)=47, R(5,7)=20。

现在让工序f从第80天（比原来晚10天，原来f最早可以第70天开始）开始，工序h从第110天（原来最早第100天开始）开始，就可以拉开资源负荷的高峰，即保证了整个工程周期内各工序所需要的工人人数，又避免了某段时间内所需要的工人人数远远少于现有人数。

现将上述具体安排如下表所示：


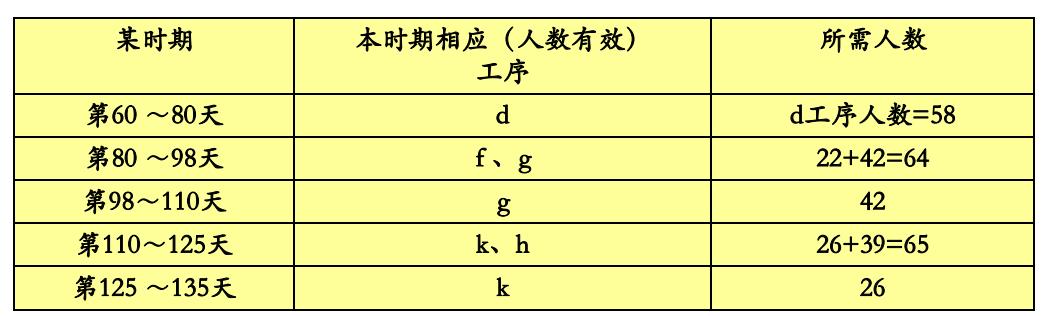
上面以人力资源的限制与要求负荷尽量均匀为例，说明了利用非关键工序总时差拉平资源负荷高峰，经过若干次调整，得到一个可行的最优计划方案的一般方法。这种方法适用与人力、物力、财力等各种资源与时间进度的综合平衡，从而选择一个最优的计划方案。
在拉平资源负荷高峰过程中，还可以采取非关键工序分段作业及减少所需资源等措施。必要时也可以根据计划目标和综合经济效益的要求，适当地拖长工程周期。

3 . 时间—费用优化
在编制网络计划过程中，研究如何使得工程完工时间短、 费用少；或者保证既定的工程完工时间的条件下，所需要的费用最少；或者在限制费用的条件下，工程完工时间最短；这就是时间—费用优化所要研究和解决的问题
为完成一项工程，所需要的费用可以分为2大类：
(1) 直接费用
是指完成这项工作直接所需的人力、资源设备费用。包括直接生产的工人的工资及附加费，设备、能源、工具及材料消耗等直接与完成工序有关的费用。
为缩短工序的作业时间，需要采取一定的技术组织措施，相应地要增加一部分直接费用。
在一定条件下和一定范围内，工序的作业时间越短，直接费用越多。
(2) 间接费用
是指管理费（如管理人员的工资），办公费等，一般按施工时间长短分摊。
在一定的生产规模内，工序的作业时间越短， 分摊的间接费用越少。

完成工程项目的直接费用、间接费用、总费用与工程完工时间的关系，一般情况下如下图所示。

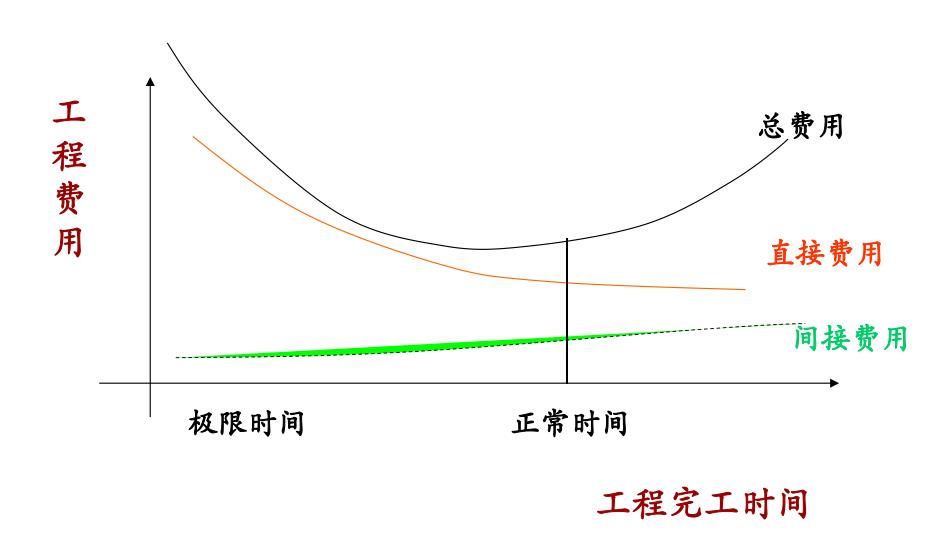
在进行时间-费用优化时，需要计算在采取各种技术措施之后， 工程项目的不同的完工时间所对应的工序总费用和工程项目所需要的总费用。
使得工程费用最低的工程完工时间为最低成本日程。
编制网络计划，无论是以降低费用为主要目的，还是以尽量缩短工程完工时间为主要目的，都要计算最低成本日程，从而提出时间-费用的优化方案。

费用与完工时间的关系

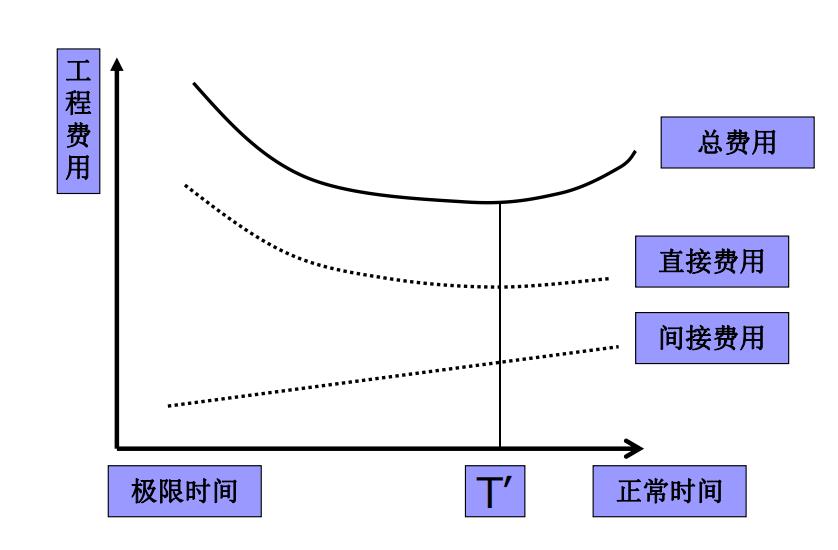
下举例说明计算最低成本日程的一种直观判断的方法。

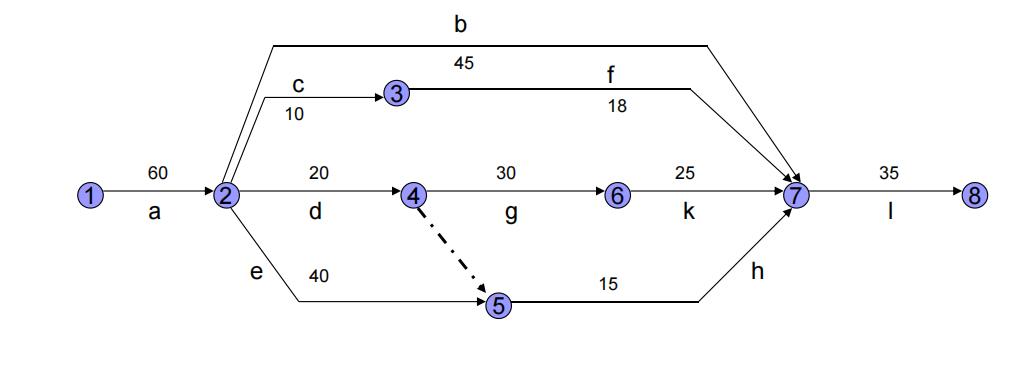
已知图中各道工序正常情况下的作业时间和极限时间，以及对应与正常时间及极限时间各工序所需要的直接费用和每缩短一天工期需要增加的直接费用，见下表：

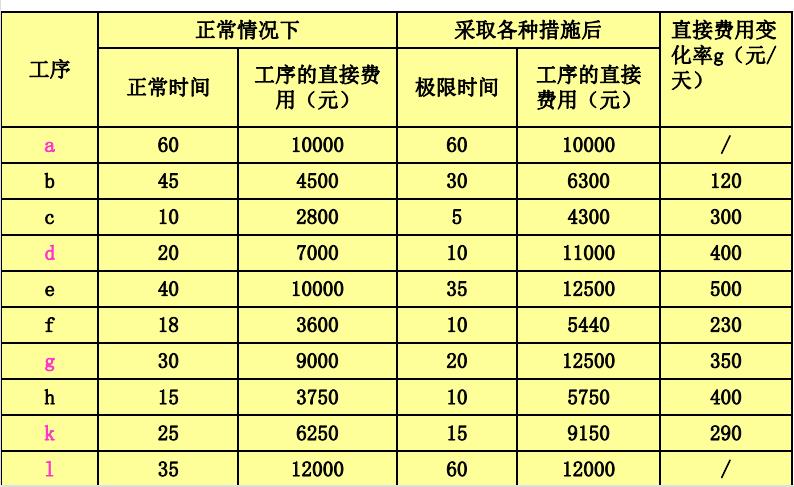
其中，缩短一天工期增加的直接费用称为直接费用变化率 ，用g表示， 它是一个平均数。
工序a、 l由于某种原因（人 员、场地负荷已饱满，为保证产品质量不宜外协），正常时间不能缩短。它们不在直接费用变动率。

若假设工程项目每天的间接费用为400元，则按前图中安排（即工程工期为170天），并根据上表的已知资料，可得工程的直接费用（各工序直接费用之和）为68900（=10000+4500+2800+7000+…+12000)元，间接费用为170*400=68000元,则总费用为136900（=68900+68000），将此方案作为第1方案。

若需要缩短第1方案的完工时间，首先要缩短关键路线上直接费用变动率最低的工序的作业时间。
如，在第1方案的关键工序a、d、g、k、l中，工序k、g的直接费用变动率最低, 且已知这2个工序的作业时间分别都只能缩短10天，则总工期可以缩短20天，即缩短到150天。
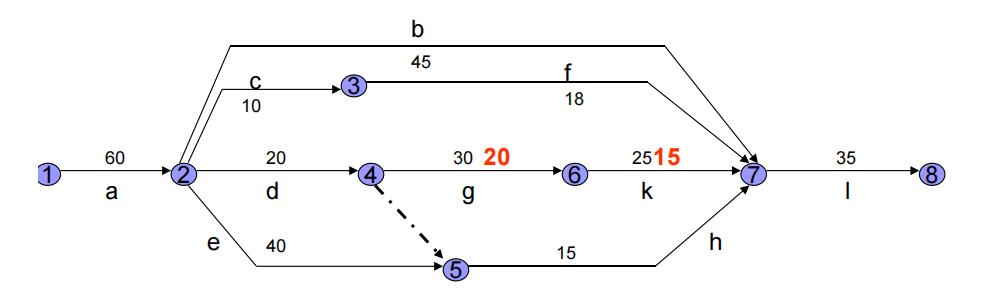工序k、g的这2个工序的作业时间分别都缩短10天
此时各工序的直接费用 = 第1方案中的直接费用 + 由于缩短工期而增加的直接费用 = 68900+35010+29010=75300
间接费用 = 第1方案的间接费用 – 由于缩短工期而节省的间接费用 = 68000-20*400 =60000。
故缩短工期后 总费用 = 75300 + 60000 = 135300（元），工 期为150天，将此方案作为第2方案。

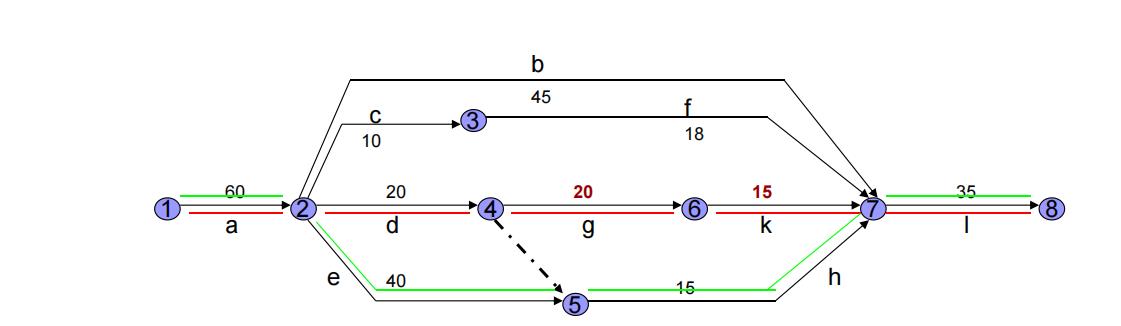
显然第2方案比第1方案好。因为工期缩短了20天，费用节省了 136900-135300 = 1600 元。
观察上图，发现第2种方案中有两条关键路线（如上图所示）。
即①→②→④→⑥→⑦→⑧ 和 ①→②→⑤→⑦→⑧。 长度均为150 若再缩短工期，考虑费用情况？

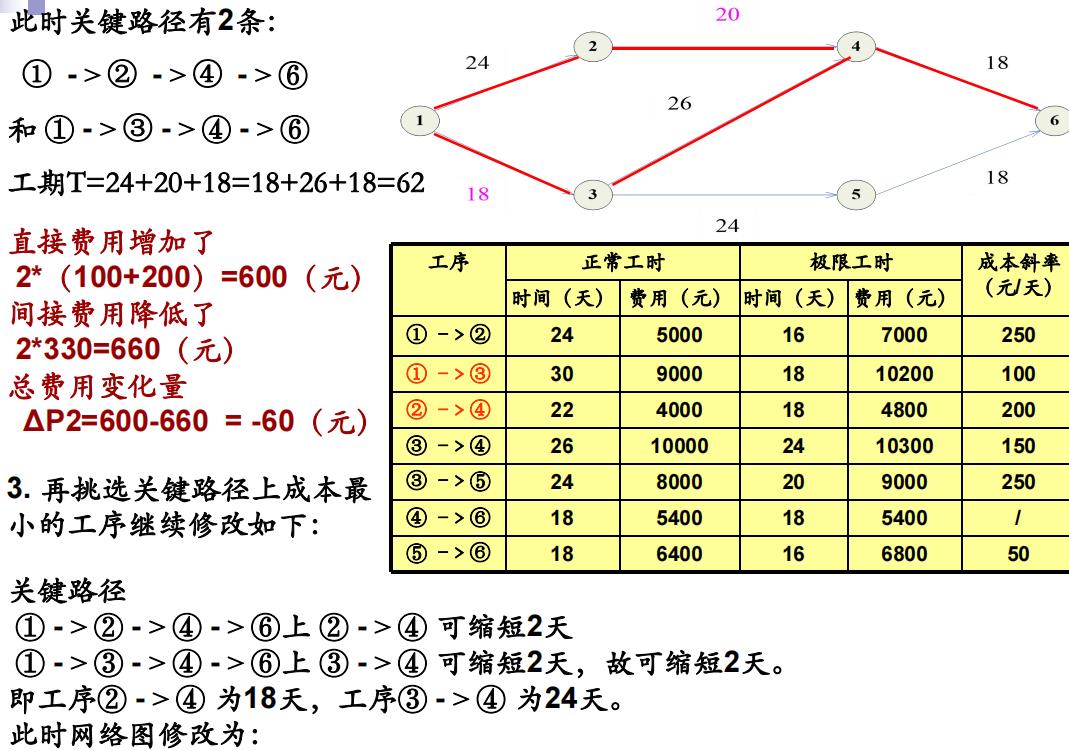
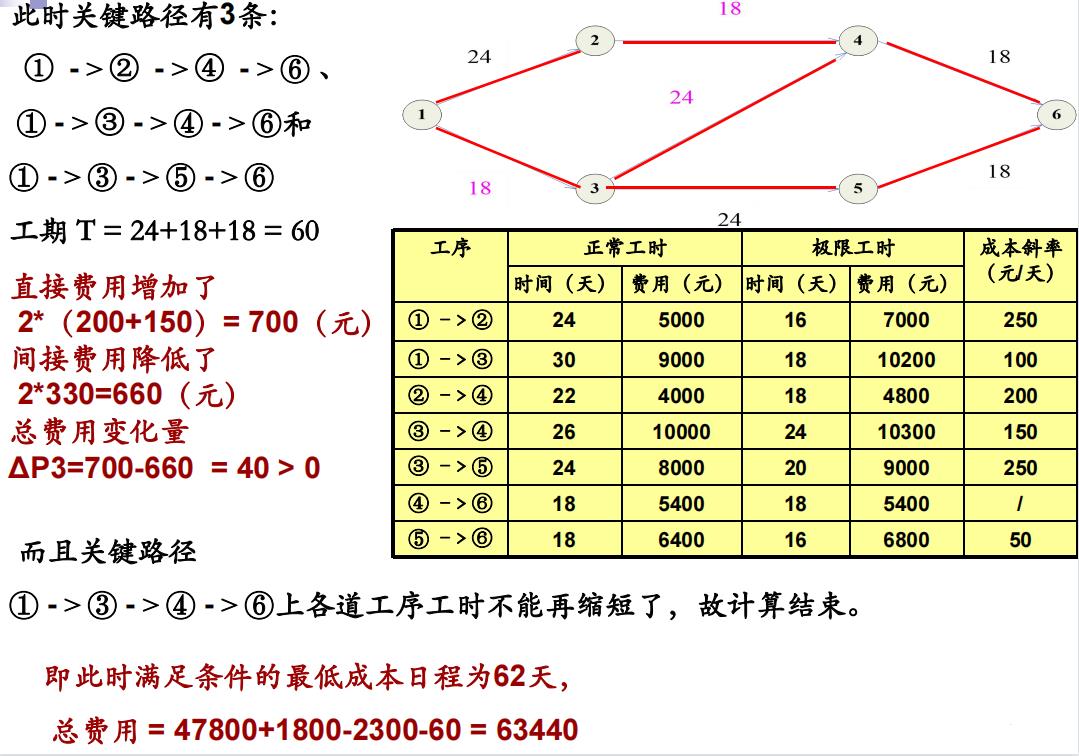
例1. 已知网络计划各工序的正常工时，极限工时及相应费用如下表所示，网络图如下图所示。


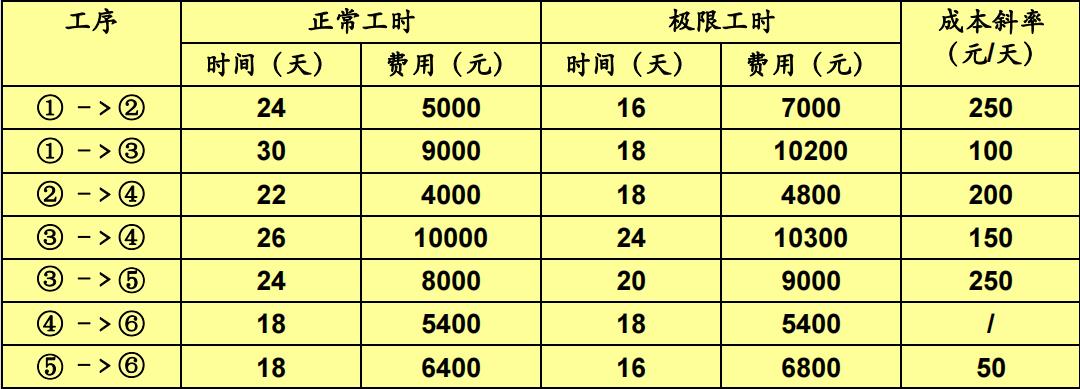
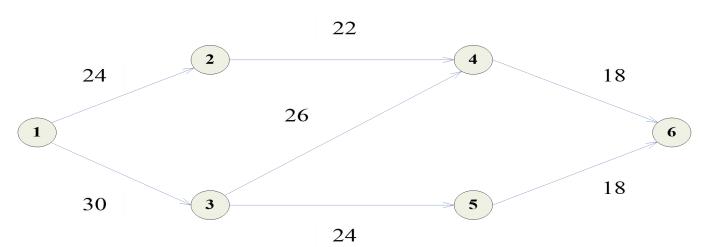
设在正常工时下，任务总间接费用为18000元，工期每缩短1天，间接费用可节省330元，求最低成本日程？

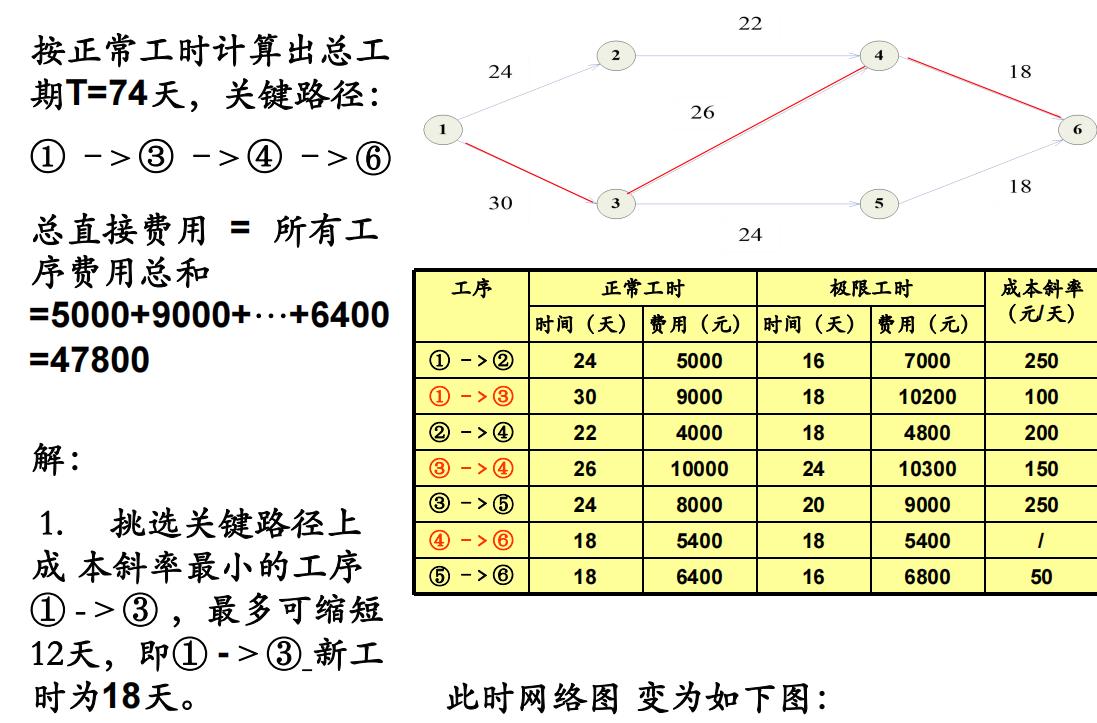
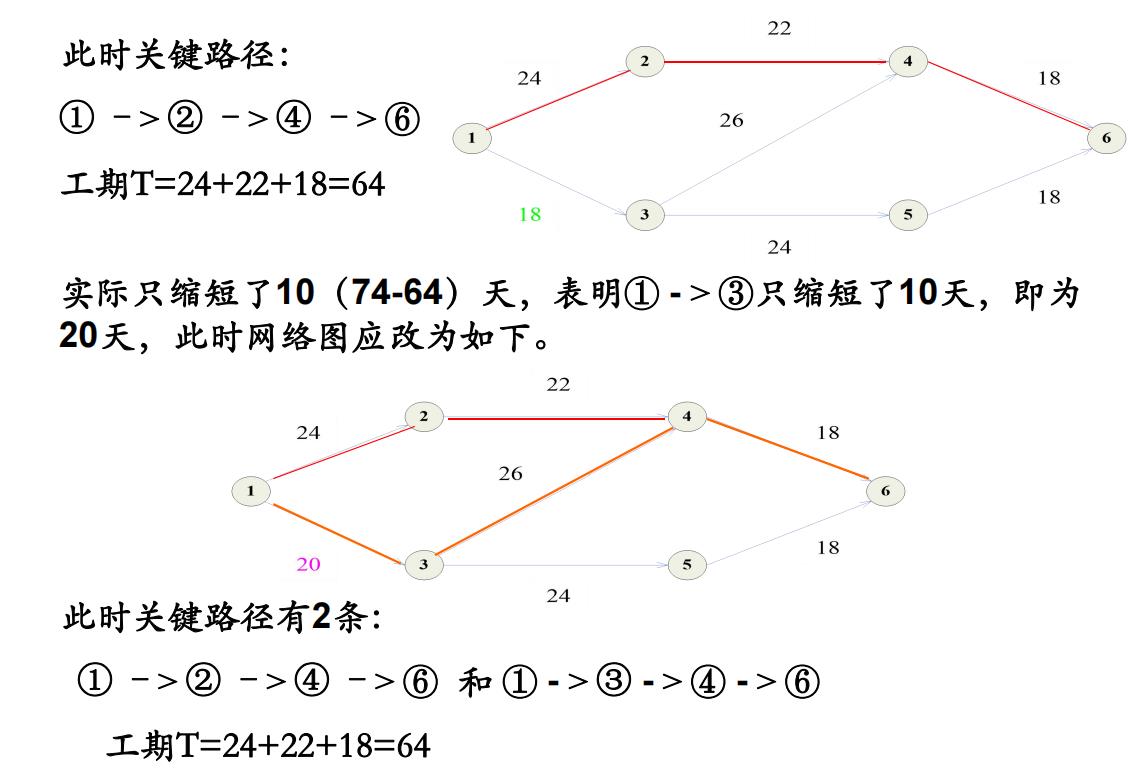
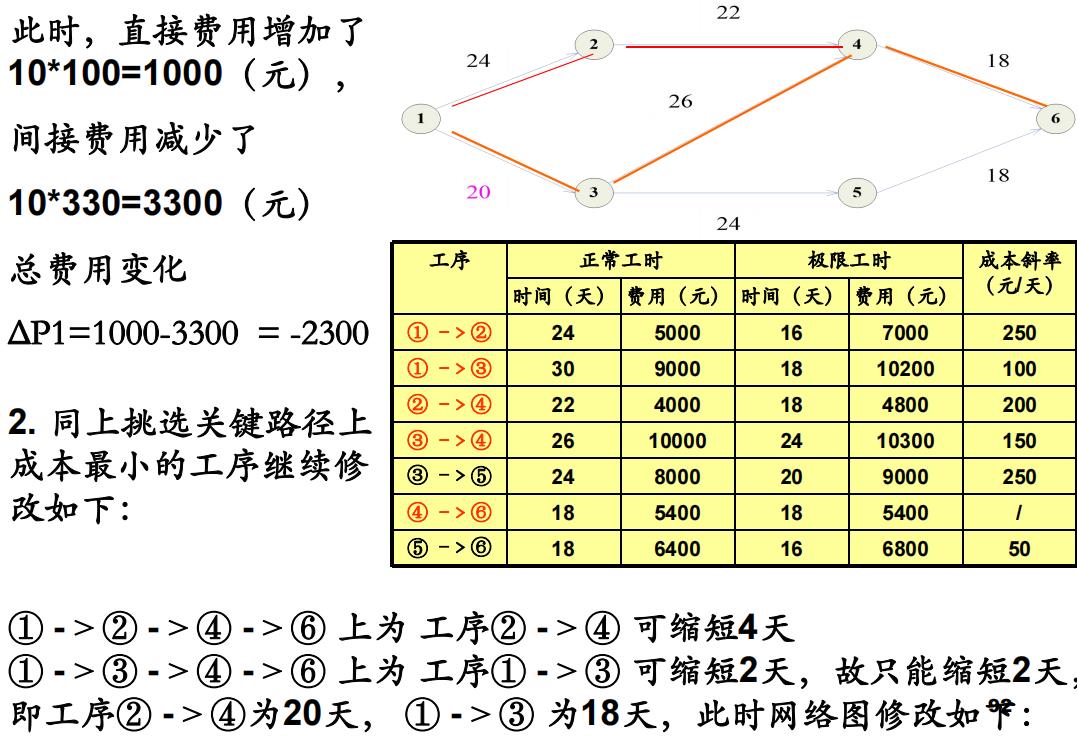
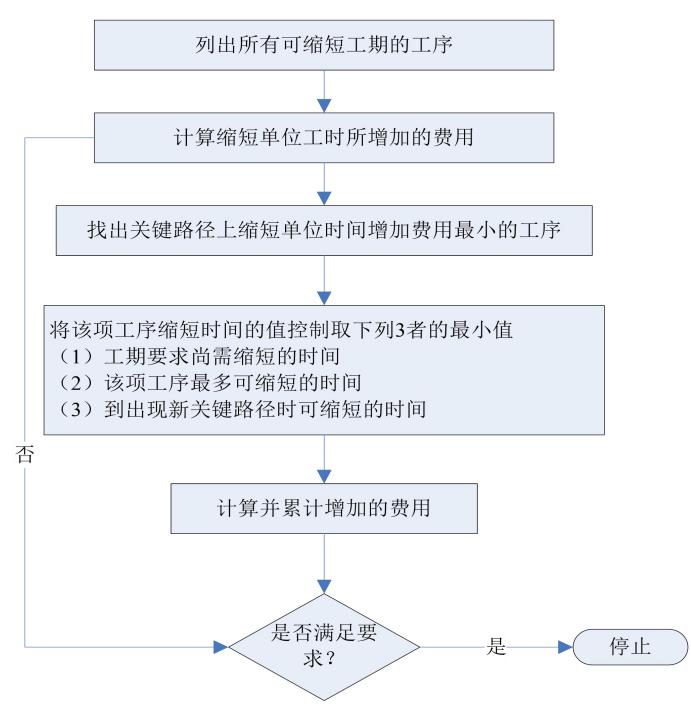
综合归纳步骤如下：
当有多条关键路径时， 往往优先考虑缩短它们的共同工序的工时