运筹学决策分析实例

Posted 2022-01-28 书槑

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了运筹学决策分析实例相关的知识，希望对你有一定的参考价值。

决策分析可以看成人与自然的博弈。

决策者需要在几个选择中做一个决策，自然环境也会有一个状态。每一个决策和自然环境状态的组合都会产生收益（可正可负），列在收益矩阵里面。最终的目标是根据一定的评判标准做出最优决策。接下来会通过英文教材上的一个例题介绍几种评判标准。

最小收益最大化准则

某公司有块地，分析师认为地里有0.25的概率有石油(oil)，0.25的概率没有(dry)。另一家公司想买这块地，但这家公司在犹豫是卖掉(sell)还是自己开发(dirll)。各种决策和状态的收益矩阵如下：

根据最小收益最大化原则，比较两种选择中的最小收益，因此选择卖地

这一标准的理由是，它提供了将获得的回报的最佳保证。例如，无论自然的真实情况是如何，出售土地的收益都不能少于90美元。这一标准是悲观的，即无论选择哪种选择，这种选择都可能出现最坏的自然状态。

当一个人与一个理性和怀有恶意的对手竞争时，这个理由是相当有效的。然而，这个标准并不经常用于和自然的博弈中，因为在这种情况下，它是一个非常保守的标准。实际上，它假设自然是一个有意识的对手，想要对决策者造成尽可能多的损害。但大自然不是一个恶意的对手，决策者不需要只关注每个选择可能最坏的回报，因此可以使用其他的评判标准。

极大似然准则

极大似然准则：确定最有可能的自然状态（具有最大先验概率的状态）。对于这种自然状态，找到具有最大回报的决策。

上面的例子中Dry具有最大的先验概率。在Dry的一列中，选择出售有最大的回报，所以选择出售土地。这一标准的吸引力在于，基于这种自然最可能发生的状态的假设，往往比假设任何其他自然状态都更能得到有利的结果。

此外，该标准并不依赖于对各自自然状态的概率的主观估计，但主要缺点是它完全忽略了许多相关的信息。除了最可能的状态，没有其他自然状态。在一个有许多可能的自然状态的问题中，最有可能的自然状态的可能性可能很小，所以只关注这种自然状态是完全没有根据的。即使在这个例子中，dry的先验概率是0.75，这个标准也忽略了当公司钻探并发现石油时，能获得700极具吸引力的回报。实际上，该标准不允许选择在低概率的大回报，无论回报多有吸引力。

贝叶斯准则

贝叶斯的决策规则：使用对各自自然状态的概率（目前的先前概率）的最佳可用估计，计算每个可能的决策方案的预期收益值。选择具有最大预期收益的决策方案。

从表16.2可以算出每个决策收益的期望值

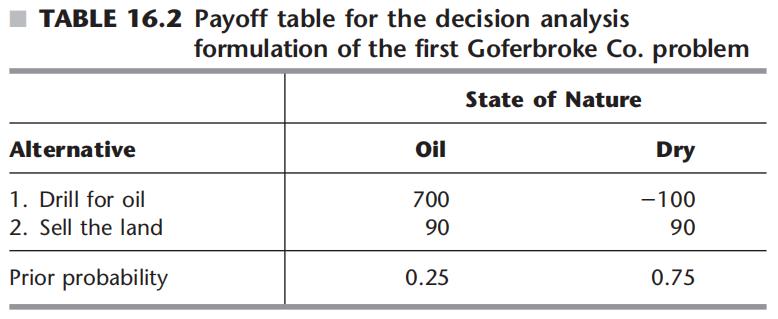
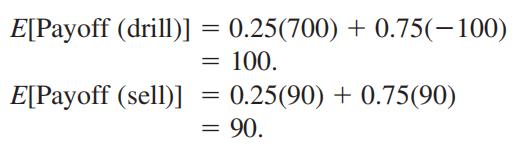
因此选择自己开发

需要注意，此选择与前两个标准下的选择形成对比。贝叶斯决策规则的最大优点是，它包含了所有可用的信息，包括所有的回报和对各自自然状态的概率的最佳可用估计。有时有人认为，这些对概率的估计在很大程度上是主观的，因此它们太不稳定，难以信任。这个论点是有一定道理的。应在每种情况下评估概率估计的合理性。在许多情况下，过去的经验和目前的证据使人们能够对可能性进行合理的估计。因此使用这些信息应该比忽视它更能为一个合理的决定提供更好的理由。此外，如下所述，可以经常进行实验，以改进这些估计值。为了评估先验概率中可能出现的不准确性的影响，通常需要进行敏感性分析，如下所述。

敏感性分析

敏感性分析通常用于运筹学的各个领域，以研究数学模型中包含的一些数字不准确时的影响。表16.2中最值得怀疑的数字是先验概率，因此我们将集中分析这些数字。

两个先验概率的总和必须等于1，因此增加其中一个概率会自动使另一个概率减少相同的量，反之亦然。该公司的管理层认为，在这片土地上拥有石油的真正机会很可能在15%到35%之间。换句话说，拥有油的真正先验概率可能在0.15到0.35之间，因此没有石油的相应先验概率可能在0.85到0.65之间。

令p = 有石油的先验概率，计算drill的期望收益

图中的斜线显示了这个期望收益与p的关系。

可以看到，drill的收益线与sell的收益线相交，交点横坐标可以算出来是0.2375。
因此，当我们试图细化对p的真实值的估计时，关键的问题是它是小于还是大于0.2375，决策会因此不同。

对于其他有两种以上决策替代方案的问题，可以应用相同类型的分析。主要的区别在于，现在对应的图形中将有超过两条收益线。如果超过两条收益线，可能有多个交叉点，决策会在交叉点的地方进行改变。

借助试验的决策

通常，可以进行额外的测试（实验）来改进对先验概率所提供的各自自然状态的概率的初步估计。这些改进的估计被称为后验概率。

在作出决定之前，一个可行方案是对土地进行地震调查，以更好地估计有石油的概率。调查成本是30美元。

地震调查通过地震探测，表明地质构造是否有利于石油存在。我们将调查的可能结果分为以下两类：

USS：不利的地震探测结果，很可能没有石油。
FSS：有利的地震探测结果，很可能有石油。

根据以往的经验，如果有石油，则发生不利地震探测的概率是

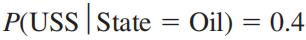
因此

同样，如果没有油（即真实状态为dry），则发生不利地震探测的概率是

因此

我们将使用这些数据来确定给定地震探测结果时各自然状态的后验概率。

后验概率的符号表示：
n = 自然界的真实状态有n种
State i = 自然界处于状态i
Finding j = 第j种实验结果
P(i) = 自然界处于状态i的先验概率
P( state i | finding j ) = 给定第j种结果时自然界处于状态i的后验概率

因此问题可以表述为：给定P(i)和P( j | i )，求P( i | j )

根据概率论的知识

写成贝叶斯公式

因此可以算出后验概率

后验概率现在取代了先验概率。通过使用表16.2中的收益并减去实验的成本，我们得到了如下结果。

如果发现不利的地震探测，将得到预期回报

如果发现有利的地震探测，将得到预期回报

由于目标是使预期收益最大化，这些结果得到表16.5所示的最佳策略。

决策树

我们将各种决策及其相应结果用决策树表示出来

在图中，第一次决策由节点a表示，节点b是表示地震调查结果的随机事件的事件节点。从事件节点b发出的两个分支代表了调查的两个可能的结果。接下来是第二个决策（节点c、d和e）及其两个可能的选择。如果决定是钻探石油，那么我们就会来到另一个事件节点(节点f、g和h)，在那里它的两个分支对应于两种可能的自然状态。

请注意，从节点a到任何终端分支（底部分支除外）的路径是由所做出的决策和决策者无法控制的随机事件决定的。这是通过决策分析所解决的问题的特征。

构建决策树的下一步是在决策树中插入数字，如图所示，没有在括号内的分支下方或上方的数字是在这些分支中发生的现金流量。对于从节点a到终端分支的每条路径，加上这些数字，可以获得该分支右侧的粗体显示的总回报。括号内的数字是随机事件发生的概率。例如从节点h来看，这些概率是这些自然状态的先验概率，因为在这种情况下还没有进行过地震调查来获得更多的信息。但是，事件节点f和g是已经进行过地震勘测（然后进行钻探）。因此，这些事件节点的概率是根据地震调查发现的自然状态的后验概率。

对于每个事件节点，通过将每个分支的预期收益（以分支末端的粗体字显示）乘以该分支的概率，然后对这些乘积求和，来计算该节点的预期收益。节点上方的黑体字记录每个决策节点的预期收益，也是通向此节点的分支的预期收益。