Matrix Derivative矩阵求导

Posted 2023-05-11

参考技术A

Welcome To My Blog
学习机器学习算法时总碰见矩阵求导,现学习一波,主要总结下
注意:这里只涉及实数的求导,研究通信的人可能接触的往往是负数求导
矩阵可以写成列向量(column vectors)或行向量(row vectors)的形式,这两种不同的形式把矩阵求导分成了两种不同的情况

机器学习中,以线性回归为例,每个输入都有多个属性,在表示属性时可以采用列向量或者行向量的形式,这两种形式会造成求导结果形式的不同.
注意是形式上的不同,因为本质上形式的不同不会影响求导结果,只不过将结果按照不同的方式组织起来,方便进一步运算
布局决定(Layout conventions)就是为了将不同形式的求导分类.分为两种布局:分子布局(numerator layout)和分母布局(denominator layout)
通俗解释,现规定 向量或者矩阵 分为原始形式和转置形式两种,比如在线性回归中我们把列向量作为属性值的原始形式,其转置形式就是行向量

将上述表格中的分子布局单独拿出来,求导结果如下

将上述表格中的分母布局单独拿出来,求导结果如下

现给出常见的求导结果,推导相关公式时可以查表
求导有链式法则(Chain Rule),但是矩阵乘积不满足交换律,所以链式法则对于matrix-by-scalar derivatives和scalar-by-matrix derivatives这两种情况不适用
下面贴出三种求导结果

之所以先展示vector-by-vector的表格,是因为所有适用于vector-by-vector求导的操作也直接适用于vector-by-scalar or scalar-by-vector这两种情况

参考:
Matrix calculus

矩阵求导

一、矩阵求导:

一般来讲，我们约定x=(x1,x2,x3....xn)的转置,这是分母布局，当然还有分子布局。常见的矩阵求导方式有：向量对向量求导，标量对向量求导，向量对标量求导。

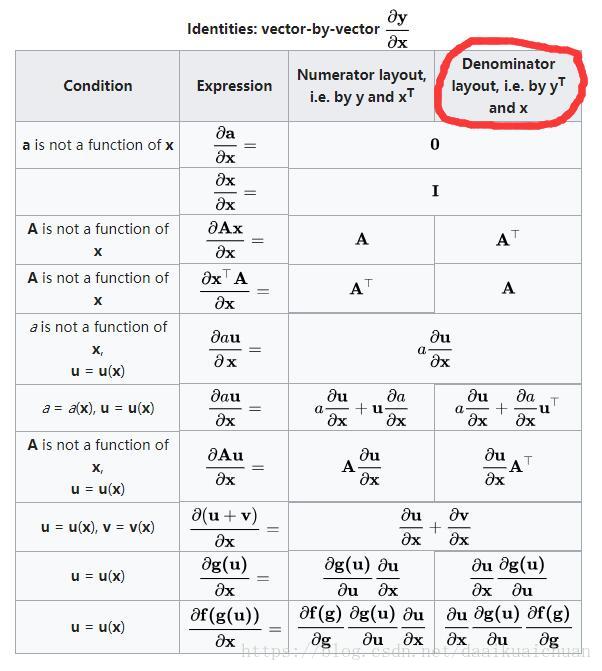
1、向量对向量求导 

       注释： Numerator layout : 分子布局

                  Denominator layout : 分母布局

                《多元统计分析》课堂，按照分子布局来讲。

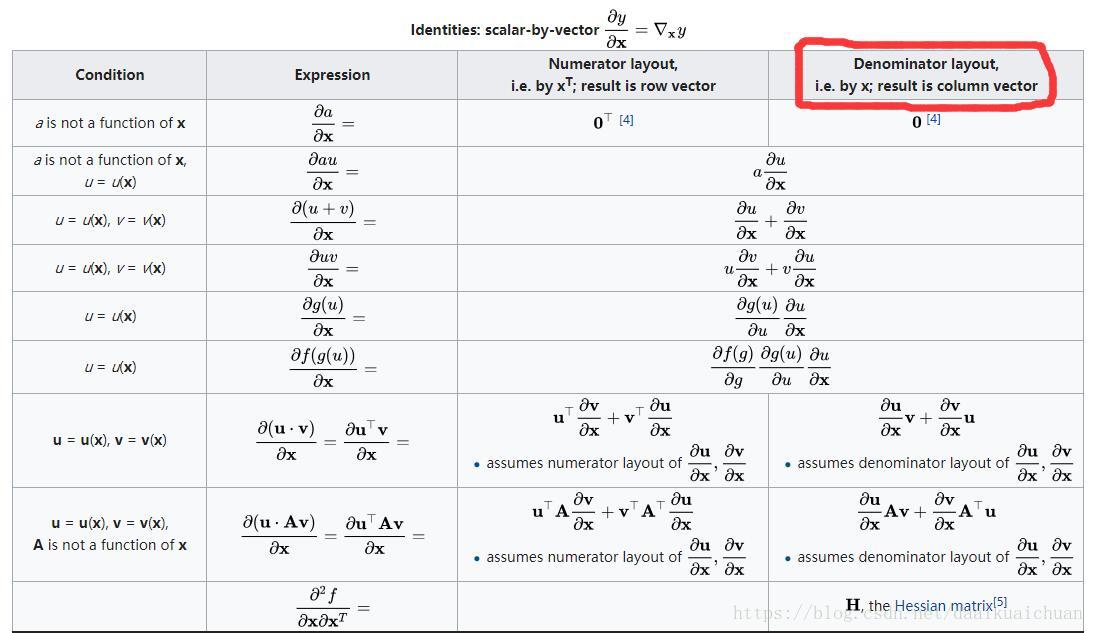
2、标量对向量求导

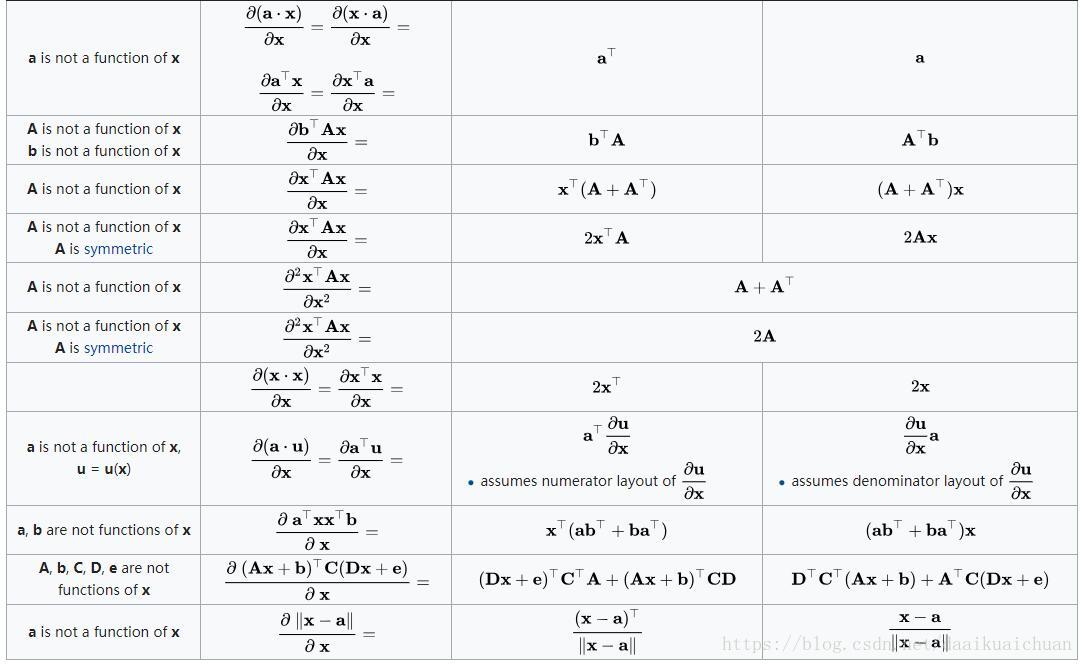
3、向量对标量求导

二、几种重要的矩阵（参见我另一篇博客：https://www.cnblogs.com/cy0628/p/13815909.html）

1、梯度（Gradient）

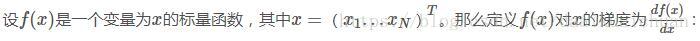
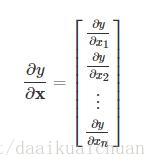
2、雅克比矩阵（Jacobian matrix）

3、海森矩阵（Hessian matrix）

三、常用的矩阵求导公式

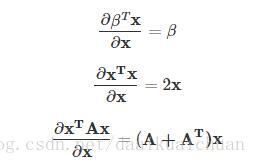
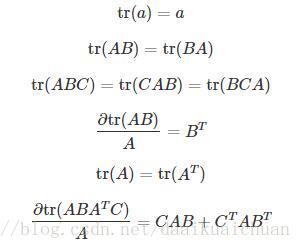
另外：我觉得知乎上某人写的挺好，现给出链接供参考：https://zhuanlan.zhihu.com/p/24709748

书籍推荐：The matrix cookbook （矩阵计算）pdf版本，适合矩阵求导和计算，下载链接：https://pan.baidu.com/s/1CzVIct_1J1pOkOIWW2o_7w

 

参考文献：The matrix cookbook 

                  https://www.cnblogs.com/jiaxinwei/p/11450561.html