怎么理解贝塞尔曲线

Posted 2023-05-02

贝塞尔曲线(Bézier curve)，又称贝兹曲线或贝济埃曲线，是应用于二维图形应用程序的数学曲线。一般的矢量图形软件通过它来精确画出曲线，贝兹曲线由线段与节点组成，节点是可拖动的支点，线段像可伸缩的皮筋，我们在绘图工具上看到的钢笔工具就是来做这种矢量曲线的。贝塞尔曲线是计算机图形学中相当重要的参数曲线，在一些比较成熟的位图软件中也有贝塞尔曲线工具，如PhotoShop等。在Flash4中还没有完整的曲线工具，而在Flash5里面已经提供出贝塞尔曲线工具。

贝塞尔曲线于1962年由法国工程师皮埃尔·贝塞尔（Pierre Bézier）所广泛发表，他运用贝塞尔曲线来为汽车的主体进行设计。贝塞尔曲线最初由Paul de Casteljau于1959年运用de Casteljau演算法开发，以稳定数值的方法求出贝兹曲线。

参考技术A 贝塞尔曲线(Bézier curve)，又称贝兹曲线或贝济埃曲线，是应用于二维图形应用程序的数学曲线。

由于用计算机画图大部分时间是操作鼠标来掌握线条的路径，与手绘的感觉和效果有很大的差别。即使是一位精明的画师能轻松绘出各种图形，拿到鼠标想随心所欲的画图也不是一件容易的事。这一点是计算机万万不能代替手工的工作，所以到目前为止人们只能颇感无奈。使用贝塞尔工具画图很大程度上弥补了这一缺憾。

贝塞尔曲线贝塞尔曲线是计算机图形图像造型的基本工具，是图形造型运用得最多的基本线条之一。它通过控制曲线上的四个点（起始点、终止点以及两个相互分离的中间点）来创造、编辑图形。其中起重要作用的是位于曲线中央的控制线。这条线是虚拟的，中间与贝塞尔曲线交叉，两端是控制端点。移动两端的端点时贝塞尔曲线改变曲线的曲率（弯曲的程度）；移动中间点（也就是移动虚拟的控制线）时，贝塞尔曲线在起始点和终止点锁定的情况下做均匀移动。注意，贝塞尔曲线上的所有控制点、节点均可编辑。这种“智能化”的矢量线条为艺术家提供了一种理想的图形编辑与创造的工具。 参考技术B 怎么理解贝塞尔曲线
“贝塞尔工具” 是所有绘图类软件中最为重要的工具之一。“贝塞尔工具”可以创建比手绘工具更为精确的直线和对称流畅的曲线。对于大多数用户而言，“贝塞尔工具”提供了最佳的绘图控制和最高的绘图准确度。
为使广大图形软件初学用户能了解“贝塞尔工具”的应用，本人这里以CorelDRAW这款软件为例，详细地剖析“贝塞尔工具”的使用方法。
“贝塞尔”是CorelDRAW中的称谓，在Photoshop、Illustrator、InDesign、QuarkXPress等软件中，称之为“钢笔工具”，虽然名称不一样，但作用是一致的，大家可以触类旁通，参照了解。
1、绘制线段
利用“贝塞尔工具”绘制线段的方式和“手绘工具”一样，能绘制直线、斜线。按住Ctrl键即限制水平、垂直或呈角度绘制线段，不同的是“贝塞尔工具”可以连续地绘制多段线段。以图01为例：先在屏幕某个位置单击鼠标以指定起始点，然后将鼠标移向（不必要按住不放）红圈1处单击指定第一个线段的终止点（在绘制多段线时，此终止点同时也为下一线段的起始点），然后继续将鼠标移向经圈2处单击，完成第二线段的绘制；以此类推，鼠标不断地在新的位置点击，就不断地产生新的线段。

必须要理解掌握的贝塞尔曲线（原创）

参考技术A

在Android开发和面试中（尤其是一些中高级岗位面试），面试官可能会问你自定义控件的详细内容，我们知道自定义控件这一块涉及到的内容很多，回答的越多越深入，那么面试的印象会更好。自定义控件涉及的内容比如测量和绘制、事件分发的处理、动画效果的渲染与实现，当然还有不得不提的贝赛尔曲线（实际上一些面试官自己都不是很理解二阶贝塞尔、三阶贝塞尔曲线等概念）。

一些朋友看到以歪果仁大佬名字定义的一些计算公式、定理就头大（比如梅涅劳斯（Menelaus）定理、塞瓦(Ceva)定理等），不得不承认我也是。本着《士兵突击》不抛弃不放弃的精神，因此就算是在难啃的骨头我们也要坚持啃下来！所以本篇文章主要介绍的是贝赛尔曲线的基本概念、在Android的应用场景以及一些思考。不考虑篇幅的情况下力求将概念和理解写的详细。

贝塞尔曲线，这个命名规则一眼看上去大概是一个叫贝塞尔的数学家发明的。但，贝塞尔曲线依据的最原始的数学公式，是在1912年在数学界广为人知的伯恩斯坦多项式。简单理解，伯恩斯坦多项式可以用来证明，在[ a, b ] 区间上所有的连续函数都可以用多项式来逼近，并且收敛性很强，也就是一致收敛。再简单点，就是一个连续函数，你可以将它写成若干个伯恩斯坦多项式相加的形式，并且，随着 n→∞，这个多项式将一致收敛到原函数，这个就是伯恩斯坦斯的逼近性质。

时光荏苒岁月如梭，镜头切换到了1959年。当时就职于雪铁龙的法国数学家 Paul de Casteljau 开始对伯恩斯坦多项式进行了图形化的尝试，并且提供了一种数值稳定的德卡斯特里奥（de Casteljau） 算法。（多数理论公式是建立在大量且系统的数学建模基础之上研究的规律性成果）根据这个算法，就可以实现 通过很少的控制点，去生成复杂的平滑曲线，也就是贝塞尔曲线 。

但贝塞尔曲线的声名大噪，不得不提到1962年就职于雷诺的法国工程师皮埃尔·贝塞尔（Pierre Bézier），他使用这种方法来辅助汽车的车体工业设计（最早计算机的诞生则是为了帮助美国海军绘制弹道图），并且广泛宣传（典型的理论联系实际并获得成功的示例），因此大家称为贝塞尔曲线 。

既然贝赛尔曲线的本质是通过数学计算公式去绘制平滑的曲线，那就可以通过数学工具进行实际求证以及解释说明。当然对其进行数学求证就没必要了，因为这些伟大的数学家们已经做过了，这里只是解释说明：

可能有些朋友还是不理解，那么这个GIF我截下其中的一张图说明，如下图：

动图里的P0、P1、P2分别代表的是上图的：P0 == A；P1 == B；P2 == C。那么这个黑色点，代表的就是F点，绿色线段的2个端点（P0-P1线段上的绿色点，代表是就是D点，P0-P2线段上的绿色点，代表是就是E点）。线段上面点的获取，必须要满足等比关系。

关于贝赛尔曲线的基本数学理论大概就是上面的内容。两个线段根据等比关系找点的贝塞尔曲线，一般也称为二阶贝塞尔曲线。

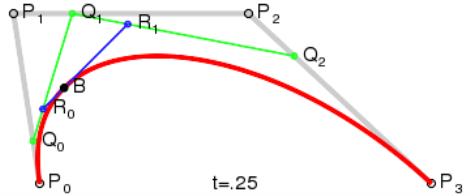
刚才说到，上面的贝赛尔曲线一般称为二阶贝塞尔曲线，既然是二阶贝塞尔曲线，那肯定有三阶贝塞尔曲线、四阶贝赛尔曲线等等。其实三阶贝塞尔与四阶贝赛尔曲线以及N阶贝赛尔曲线曲线的规则都是一样的，都是先在线段上找点，这个点必须要满足等比关系，然后依次连接，下面是三阶贝赛尔曲线的解释说明：

整一个三阶贝赛尔曲线的动作加起来就是下面的一张动图：

那么四阶贝赛尔曲线的实现步骤也是一样的，平面上先选取5个点（5点4线）、依次选点（满足等比关系）、依次连接、根据计算规则找到所有的点（逐个连接）。。。。。。

貌似都是从二阶贝塞尔曲线说起的，那么一阶贝赛尔又是怎么样的？一阶贝赛尔如图：

可以看到一阶贝赛尔是一条直线！因此，N阶贝赛尔不仅可以画平滑的曲线也可以画直线，因此自定义控件画直线又多了一种可选择的方式，但是一般用贝赛尔主要是画曲线，这里只是提供了一种别的解决思路；另外，在Android属性动画，系统为我们提供了一个PathInterpolator插值器。这个PathInterpolator里面就有贝塞尔曲线的身影。有兴趣的小伙伴也可以去了解一下。

未完待续。。。

如果这篇文章对您有开发or学习上的些许帮助，希望各位看官留下宝贵的star，谢谢。