关于多普勒与采样定理的问题 大侠快来帮忙
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了关于多普勒与采样定理的问题 大侠快来帮忙相关的知识,希望对你有一定的参考价值。
采样定理为取样频率必须大于所采对象运动频率的2倍。fd<1/2PRF其中的fd为对象的运动频率 比如电扇转动频率 而多普勒成像也应用了此原理 并把fd附予了 发射频率与接收频率的差 第一个问题 此时的fd能代表血细胞的运动频率吗 而且血液的运动形式也不同于电扇 应该没有周期性吧 也就没有频率吧
再者根据多普勒测速定理 v=fd*c/2f0cos 当探头发射出脉冲后 超声波打在特定深度的血细胞上 定会反射回另一个频率的超声波 并被接受(经过特定时间) 前后两个频率之差即fd 速度应该就能求出来了(哪怕只发射一组脉冲) 为什么还要考虑采样定理呢
能说的通俗一点吗
就算一个信号没有周期,它也有频率,只不过频率是无穷大,就只有一个周期而已。 我觉得只要是要采样,你就必须要遵守采样定理,采样定理都不满足,怎么能采到真正想要的得到的值。 参考技术A 体现在space_time steering vector里的多普勒导向矢量上。 space_time steering vector = kron(space steering vector, doppler steering vector)。 kron表示kronecker积。 当PRF小于多普勒频率时将不满足来奎斯特采样定理,从而出现模糊现象。
数字信号处理4:采样定理
文章目录
采样定理又称奈奎斯特定理,它规定了连续信号抽样成为离散信号时的采样率与信号最大频率之间的关系,那就是:
对于连续信号 x ( t ) x(t) x(t)进行抽样时,抽样信号的最小频率 p ( t ) p(t) p(t)的频率要大于 x ( t ) x(t) x(t)的最大频率的2倍,采样得出的信号 x [ n ] x[n] x[n]才能还原出原始信号 x ( t ) x(t) x(t)。
这一点其实容易想明白,比如下面三个信号:
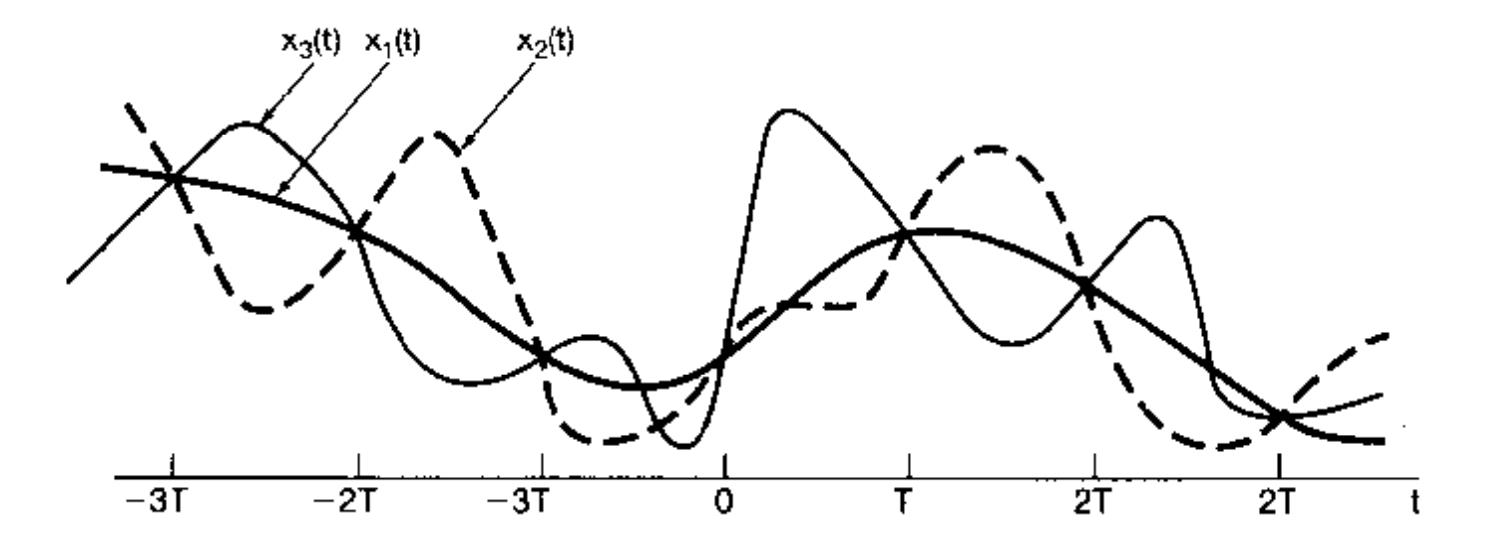
如果在T的整数倍处对三个信号采样,你会发现采样出的信号是完全一致的,这就导致你无法还原原始信号。因此,我们要明确采样频率和原信号的中包含的最高频率分量的关系。
通常来说,我们对于一个连续信号采样时,是截取
x
(
t
)
x(t)
x(t)在某一时刻的值,因此不妨将整个采样过程看做
x
(
t
)
x(t)
x(t)与
p
(
t
)
p(t)
p(t)的乘积,其中
p
(
t
)
p(t)
p(t)是梳妆函数,它是一系列冲激信号的延时叠加:
p
(
t
)
=
∑
n
=
−
∞
+
∞
δ
(
t
−
n
T
)
p(t) = \\sum_n = -\\infty^+\\infty \\delta(t-nT)
p(t)=n=−∞∑+∞δ(t−nT)
它的时域图像如下:
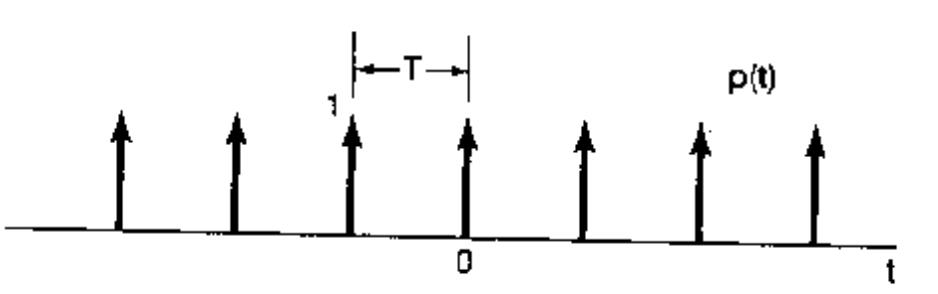
对它做傅里叶变换得到频域图像如下:
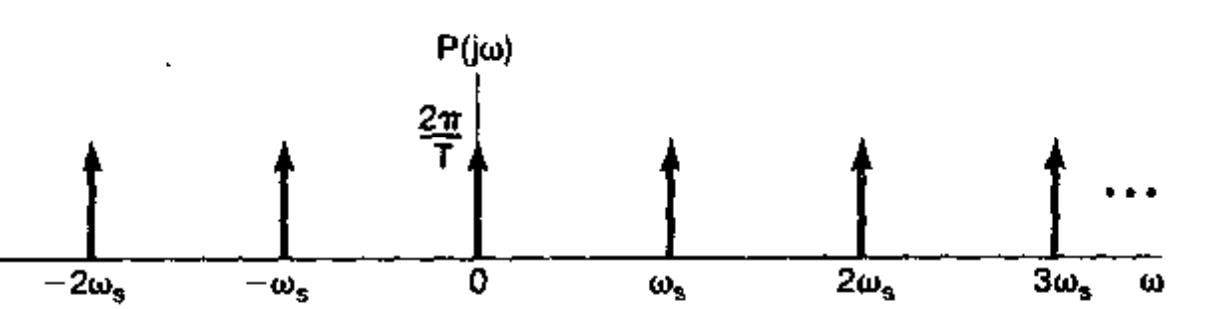
对应的表达式为
P ( j w ) = ∑ k = − ∞ + ∞ δ ( w − k w s ) P(jw) = \\sum_k=-\\infty^+\\infty\\delta(w - kw_s) P(jw)=k=−∞∑+∞δ(w−kws)
而对于
x
(
t
)
x(t)
x(t),我们需要假设它是一个带限信号,意味着它在频率上是有界的(否则就会发生频谱混叠)。它的频域图像如下:
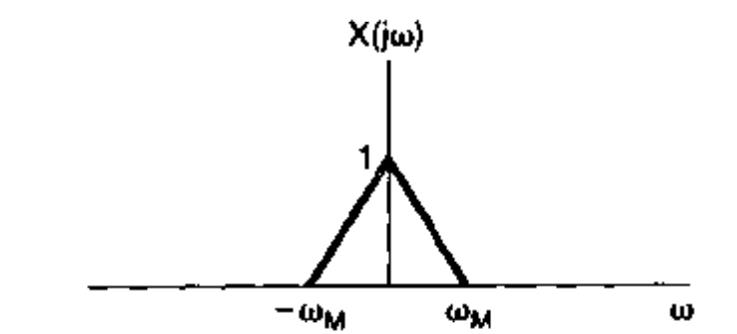
以上就是我们对输入信号 x ( t ) x(t) x(t)和采样信号 p ( t ) p(t) p(t)的直观认识,接下来推导采样定理。
1. 卷积定理
之前我们有说过,时域卷积等于频域相乘,频域相乘等于时域卷积。这个结论对于我们推导采样定理以及建立对傅里叶变换后的频域的认识非常重要。因此先推导这个结论。
假设有信号
y
(
t
)
=
x
(
t
)
∗
h
(
t
)
=
∫
−
∞
+
∞
x
(
τ
)
h
(
t
−
τ
)
d
τ
y(t) = x(t) * h(t) = \\int_-\\infty^+\\inftyx(\\tau)h(t-\\tau)d\\tau
y(t)=x(t)∗h(t)=∫−∞+∞x(τ)h(t−τ)dτ
直接对
y
(
t
)
y(t)
y(t)做傅里叶变换:
Y
(
j
w
)
=
∫
−
∞
+
∞
[
∫
−
∞
+
∞
x
(
τ
)
h
(
t
−
τ
)
d
τ
]
e
−
j
w
t
d
t
Y(jw) = \\int_-\\infty^+\\infty[\\int_-\\infty^+\\inftyx(\\tau)h(t-\\tau)d\\tau]e^-jwtdt
Y(jw)=∫−∞+∞[∫−∞+∞x(τ)h(t−τ)dτ]e−jwtdt
交换积分次序,且由于
x
(
τ
)
x(\\tau)
x(τ)与
t
t
t无关
= ∫ − ∞ + ∞ x ( τ ) [ ∫ − ∞ + ∞ h ( t − τ ) e − j w t d t ] d τ = \\int_-\\infty^+\\inftyx(\\tau)[\\int_-\\infty^+\\inftyh(t-\\tau)e^-jwtdt]d\\tau =∫−∞+∞x(τ)[∫−∞+∞h(t−τ)e−jwtdt]dτ
根据傅里叶变换的时移性质:
若
x
(
t
)
x(t)
x(t)的傅里叶变换为
X
(
j
w
)
X(jw)
X(jw),则
x
(
t
−
τ
)
x(t-\\tau)
x(t−τ)的傅里叶变换为:
∫
−
∞
+
∞
x
(
t
−
τ
)
e
−
j
w
t
d
t
=
∫
−
∞
+
∞
x
(
t
−
τ
)
e
−
j
w
(
t
−
τ
)
e
−
j
w
τ
d
t
=
e
−
j
w
τ
X
(
j
w
)
\\int_-\\infty^+\\inftyx(t-\\tau)e^-jwtdt = \\int_-\\infty^+\\inftyx(t-\\tau)e^-jw(t-\\tau)e^-jw\\taudt=e^-jw\\tauX(jw)
∫−∞+∞x(t−τ)e−jwtdt=∫−∞+∞x(t−τ)e−jw(t−τ)e−jwτdt=e−jwτX(jw)
因此,上式中方括号内的部分就可以用时移定理处理。
= ∫ − ∞ + ∞ x ( τ ) [ e − j w τ H ( j w ) ] d τ = \\int_-\\infty^+\\inftyx(\\tau)[e^-jw\\tauH(jw)]d\\tau =∫−∞+∞x(τ)[e−jwτH(jw)]dτ
且 H ( j w ) H(jw) H(jw)与 τ \\tau τ无关,可移出积分外。
= H ( j w ) ∫ − ∞ + ∞ x ( τ ) e − j w τ d τ = H ( j w ) X ( j w ) = H(jw)\\int_-\\infty^+\\inftyx(\\tau)e^-jw\\taud\\tau = H(jw)X(jw) =H(jw)∫−∞+∞x(τ)e−jwτdτ=H(jw)X(jw)
故而
y
(
t
)
=
x
(
t
)
∗
h
(
t
)
y(t) = x(t) * h(t)
y(t)=x(t)∗h(t)
的傅里叶变换为
Y
(
w
)
=
X
(
j
w
)
H
(
j
w
)
Y(w) = X(jw)H(jw)
Y(w)=X(jw)H(jw)
对于频域卷积的情况,由于情况是对称的,所以不再单独推导。
2. 采样定理推导
之前的结论是,对于采样过程,可以写成
x
p
(
t
)
=
x
(
t
)
p
(
t
)
x_p(t) = x(t)p(t)
xp(t)=x(t)p(t)
那么,对于 x p ( t ) x_p(t) xp(t)的傅里叶变换 X p ( j w ) X_p(jw) Xp(jw),就是频域卷积 X ( j w ) ∗ P ( j w ) X(jw)*P(jw) X(jw)∗P(j关于用FFT分析信号频谱的问题