如图，向方格纸（方格边长为a）内投掷直径为2r的硬币（2r＜a)，求硬币不与线条相交的概率。

Posted 2023-04-29

参考技术A 上面的做的对，不过没解释清楚 。——根据题意，先把硬币看成一点（圆心）。因此圆心落进任意一个方格的概率始终为1。 参考技术B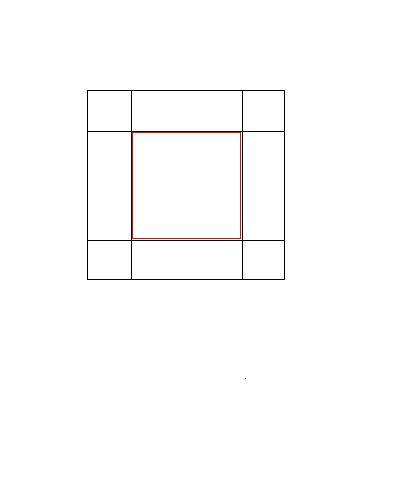

 

只要圆心扔在红色范围内，那这个圆与线条就不相交。黑色正方形是题内的一个方格；红色正方形边长为(a-r)，四条边距离黑色正方型的四条边分别为r。红色正方形和黑色正方形的面积分别为(a-r)²和a²,所以硬币不与线条相交的概率为(a-r)²/a²

 

本回答被提问者和网友采纳

P1004 方格取数

设有 N×N 的方格图，我们在其中的某些方格中填入正整数，而其它的方格中则放入数字0。

某人从图中的左上角出发，可以向下行走，也可以向右行走，直到到达右下角。
在走过的路上，他可以取走方格中的数（取走后的方格中将变为数字0）。
共走了两次，试找出两条这样的路径，使得取得的数字和为最大。

输入格式
第一行为一个整数N，表示 N×N 的方格图。
接下来的每行有三个整数，第一个为行号数，第二个为列号数，第三个为在该行、该列上所放的数。

一行“0 0 0”表示结束。
输出格式
输出一个整数，表示两条路径上取得的最大的和。

数据范围
N≤10

分析：一开始以为可以用两次二维DP，然后试了一下，在某些情况下是不行的，WA
正确方法是同时对两条路径进行DP
状态表示：f[i1][j1][i2][j2] 分别表示两条路线的坐标，可以发现，既然是同时走的，而且每次只走一步，那么 i1 + j1 == j2 + j2 一定成立，可以用一个变量k来表示横纵坐标的和，
?????那么就变成了3维，f[k][i1][i2];
状态计算：考虑到达这个状态的最后一步操作，每条路径有向下走和向右走两种走法，一共4种状态，特判二者当前重合的情况， 取max即可

Code:

#include <bits/stdc++.h>

using namespace std;

const int N = 12;

int n;
int w[N][N],f[2*N][N][N];

int main()
{
    cin >> n;
    int r,c,x;
    while(cin >> r >> c >> x, r||c||x)
    {
        w[r][c] = x;
    }
    
    for(int k = 2;k <= 2*n;k++)
        for(int i1 = 1;i1 <= n;i1++)
            for(int i2 = 1;i2 <= n;i2++)
            {
                int j1 = k - i1,j2 = k - i2;
                if(j1 >= 1 && j1 <= n && j2 >= 1 && j2 <= n)
                {
                    int t = w[i1][j1];
                    if(i1 != i2) t += w[i2][j2];
                    int &x = f[k][i1][i2];
                    x = max(x, f[k-1][i1-1][i2-1] + t);
                    x = max(x, f[k-1][i1-1][i2] + t);
                    x = max(x, f[k-1][i1][i2-1] + t);
                    x = max(x, f[k-1][i1][i2] + t);
                }
            }
            
    cout << f[2*n][n][n] << endl;
    return 0;
}