>>> import numpy as np
>>> x=np.matrix([[1,2,3],[4,5,6]])
>>> y=np.matrix([1,2,3,4,5,6])
>>> print(x)
[[1 2 3]
 [4 5 6]]
>>> print(y)
[[1 2 3 4 5 6]]
>>> x[1]    #注意，对矩阵来说，X[1,1]和X[1][1]的含义不一样，后者异常
matrix([[4, 5, 6]])
>>> x[1,1]    #X[1,1]返回行下标和列下标都为1的元素
5
>>> y[0]
matrix([[1, 2, 3, 4, 5, 6]])
>>> y[0,1]
2

2.矩阵转置

>>> x
matrix([[1, 2, 3],
        [4, 5, 6]])
>>> y
matrix([[1, 2, 3, 4, 5, 6]])
>>> print(x.T,y.T,sep='\\n\\n')
[[1 4]
 [2 5]
 [3 6]]

[[1]
 [2]
 [3]
 [4]
 [5]
 [6]]
>>> x.T
matrix([[1, 4],
        [2, 5],
        [3, 6]])

3.查看矩阵特征

>>> x=np.matrix([[1,2,3],[4,5,6]])
>>> print(x.mean(),end='\\n====\\n')    #所有元素平均值
3.5
====
>>> print(x.mean(axis=0),end='\\n===\\n')    #纵向平均值
[[2.5 3.5 4.5]]
===
>>> print(x.mean(axis=0).shape,end='\\n====\\n')
(1, 3)
====
>>> print(x.mean(axis=1),end='\\n====\\n')    #横向平均值
[[2.]
 [5.]]
====
>>> print(x.sum(),end='\\n====\\n')    #所有元素之和
21
====
>>> print(x.max(axis=1))    #横向最大值
[[3]
 [6]]
>>> print(x.argmax(axis=1))    #横向最大值的下标
[[2]
 [2]]
>>> print(x.max(axis=0),end='\\n====\\n')    #纵向最大值
[[4 5 6]]
====
>>> print(x.diagonal(),end='\\n====\\n')    #对角线元素
[[1 5]]
====
>>> print(x.nonzero())    #非零元素下标，分别返回行下标和列下标
(array([0, 0, 0, 1, 1, 1], dtype=int64), array([0, 1, 2, 0, 1, 2], dtype=int64))

4.矩阵乘法

>>> A=np.matrix([[1,2,3],[4,5,6]])
>>> print(A)
[[1 2 3]
 [4 5 6]]
>>> B=np.matrix([[1,2],[3,4],[5,6]])
>>> print(B)
[[1 2]
 [3 4]
 [5 6]]
>>> C=A*B
>>> print(C)
[[22 28]
 [49 64]]
>>> A.shape,B.shape,C.shape
((2, 3), (3, 2), (2, 2))

5.计算相关系数矩阵

相关系数矩阵是一个对称矩阵，其中对角线上的元素都是1，表示自相关系数
非对角线元素表示互相关系数，每个元素的绝对值都小于等于1，反应变量变化趋势的相似程度
例如，如果相关系数矩阵中非对角线元素大于0，表示两个信号正相关，其中一个信号变大时另一个信号也变大，变化方向一致，或者说一个信号的变化对另一个信号的影响是正面或者积极的
相关系数的绝对值越大，表示两个信号互相影响的程度越大

>>> print(np.corrcoef([1,2,3,4],[4,3,2,1]))    #负相关，变化方向相反
[[ 1. -1.]
 [-1.  1.]]
>>> print(np.corrcoef([1,2,3,4],[8,3,2,1]))    #负相关，变化方向相反
[[ 1.         -0.91350028]
 [-0.91350028  1.        ]]
>>> print(np.corrcoef([1,2,3,4],[1,2,3,4]))     #正相关，变化方向一致                        
[[1. 1.]
 [1. 1.]]
>>> print(np.corrcoef([1,2,3,4],[1,2,3,40]))       #正相关，变化趋势接近                   
[[1.        0.8010362]
 [0.8010362 1.       ]]

6.计算方差、协方差、标准差

>>> print(np.cov([1,1,1,1,1]))  #方差（自身协方差）                      
0.0
>>> print(np.std([1,1,1,1,1]))    #标准差
0.0
>>> print(np.cov([1,2,1,4,1]))                        
1.7000000000000002
>>> print(np.std([1,2,1,4,1]))                        
1.1661903789690602
>>> x=[-2.1,-1,4.3]                        
>>> y=[3,1.1,0.12]                         
>>> X=np.vstack((x,y))     #垂直堆叠矩阵                    
>>> print(X)                         
[[-2.1  -1.    4.3 ]
 [ 3.    1.1   0.12]]                         
>>> print(np.cov(X))     #协方差                    
[[11.71       -4.286     ]
 [-4.286       2.14413333]]
>>> print(np.cov(x,y))                        
[[11.71       -4.286     ]
 [-4.286       2.14413333]]
>>> print(np.cov(x))                        
11.709999999999999
>>> print(np.cov(y))                        
2.1441333333333334
>>> print(np.std(x))        #标准差                
2.794041278626117
>>> print(np.std(x+y))      #同x标准差                
2.2071223094538484
>>> print(np.std(X,axis=1))  #横向标准差，相当于x，y标准差                       
[2.79404128 1.19558447]
>>> print(np.std(x))    #x标准差方差                    
2.794041278626117
>>> print(np.std(X,axis=0))                       
[2.55 1.05 2.09]

7.行列扩展

>>>data=np.matrix([np.random.randint(1,10,5) for _ in range(6)])
>>>newcols=np.matrix([np.random.randint(1,10,2) for _ in range(6)])
>>>newrows=np.matrix([np.random.randint(1,10,5) for _ in range(3)])
>>>data
matrix([[4, 5, 8, 1, 1],
        [1, 5, 2, 1, 5],
        [5, 1, 2, 1, 9],
        [6, 1, 6, 6, 7],
        [1, 1, 5, 9, 1],
        [8, 8, 6, 2, 4]])
>>>newcols
matrix([[4, 2],
        [7, 3],
        [6, 1],
        [1, 1],
        [3, 8],
        [8, 9]])
>>>newrows
matrix([[4, 1, 3, 5, 7],
        [9, 3, 9, 8, 9],
        [8, 7, 5, 8, 5]])
>>>np.c_[data,newcols]    #在data的右侧（列）加入newcols
matrix([[4, 5, 8, 1, 1, 4, 2],
        [1, 5, 2, 1, 5, 7, 3],
        [5, 1, 2, 1, 9, 6, 1],
        [6, 1, 6, 6, 7, 1, 1],
        [1, 1, 5, 9, 1, 3, 8],
        [8, 8, 6, 2, 4, 8, 9]])
>>>np.c_[newcols,data]    #在data左侧（列）加入newcols
matrix([[4, 2, 4, 5, 8, 1, 1],
        [7, 3, 1, 5, 2, 1, 5],
        [6, 1, 5, 1, 2, 1, 9],
        [1, 1, 6, 1, 6, 6, 7],
        [3, 8, 1, 1, 5, 9, 1],
        [8, 9, 8, 8, 6, 2, 4]])
>>>np.r_[data,newrows]    #在data的下面（行）加入newrows
matrix([[4, 5, 8, 1, 1],
        [1, 5, 2, 1, 5],
        [5, 1, 2, 1, 9],
        [6, 1, 6, 6, 7],
        [1, 1, 5, 9, 1],
        [8, 8, 6, 2, 4],
        [4, 1, 3, 5, 7],
        [9, 3, 9, 8, 9],
        [8, 7, 5, 8, 5]])
>>>np.r_[newrows,data]    #在data的上面（行）加入newrows
matrix([[4, 1, 3, 5, 7],
        [9, 3, 9, 8, 9],
        [8, 7, 5, 8, 5],
        [4, 5, 8, 1, 1],
        [1, 5, 2, 1, 5],
        [5, 1, 2, 1, 9],
        [6, 1, 6, 6, 7],
        [1, 1, 5, 9, 1],
        [8, 8, 6, 2, 4]])
>>>np.r_[data,newrows,newrows]
matrix([[4, 5, 8, 1, 1],
        [1, 5, 2, 1, 5],
        [5, 1, 2, 1, 9],
        [6, 1, 6, 6, 7],
        [1, 1, 5, 9, 1],
        [8, 8, 6, 2, 4],
        [4, 1, 3, 5, 7],
        [9, 3, 9, 8, 9],
        [8, 7, 5, 8, 5],
        [4, 1, 3, 5, 7],
        [9, 3, 9, 8, 9],
        [8, 7, 5, 8, 5]])
>>> np.insert(data,0,newrows,axis=0)    #在data的第0行插入newrows
matrix([[4, 1, 3, 5, 7],
        [9, 3, 9, 8, 9],
        [8, 7, 5, 8, 5],
        [4, 5, 8, 1, 1],
        [1, 5, 2, 1, 5],
        [5, 1, 2, 1, 9],
        [6, 1, 6, 6, 7],
        [1, 1, 5, 9, 1],
        [8, 8, 6, 2, 4]])
>>> np.insert(data,3,newrows,axis=0)    #在data的第三行插入newrows
matrix([[4, 5, 8, 1, 1],
        [1, 5, 2, 1, 5],
        [5, 1, 2, 1, 9],
        [4, 1, 3, 5, 7],
        [9, 3, 9, 8, 9],
        [8, 7, 5, 8, 5],
        [6, 1, 6, 6, 7],
        [1, 1, 5, 9, 1],
        [8, 8, 6, 2, 4]])
>>> np.insert(data,4,newcols.T,axis=1)    #在data的第四列插入newcols
matrix([[4, 5, 8, 1, 4, 2, 1],
        [1, 5, 2, 1, 7, 3, 5],
        [5, 1, 2, 1, 6, 1, 9],
        [6, 1, 6, 6, 1, 1, 7],
        [1, 1, 5, 9, 3, 8, 1],
        [8, 8, 6, 2, 8, 9, 4]])
>>> np.insert(data,1,newcols.T,axis=1)    #在data的第一列插入newcols
matrix([[4, 4, 2, 5, 8, 1, 1],
        [1, 7, 3, 5, 2, 1, 5],
        [5, 6, 1, 1, 2, 1, 9],
        [6, 1, 1, 1, 6, 6, 7],
        [1, 3, 8, 1, 5, 9, 1],
        [8, 8, 9, 8, 6, 2, 4]])
>>> np.row_stack((data,newrows))    #垂直（行）堆叠矩阵，与np.vstack((data,newrows))
matrix([[4, 5, 8, 1, 1],
        [1, 5, 2, 1, 5],
        [5, 1, 2, 1, 9],
        [6, 1, 6, 6, 7],
        [1, 1, 5, 9, 1],
        [8, 8, 6, 2, 4],
        [4, 1, 3, 5, 7],
        [9, 3, 9, 8, 9],
        [8, 7, 5, 8, 5]])
>>> np.column_stack((data,newcols))    #横着（列）堆叠矩阵
matrix([[4, 5, 8, 1, 1, 4, 2],
        [1, 5, 2, 1, 5, 7, 3],
        [5, 1, 2, 1, 9, 6, 1],
        [6, 1, 6, 6, 7, 1, 1],
        [1, 1, 5, 9, 1, 3, 8],
        [8, 8, 6, 2, 4, 8, 9]])

8.常用变量

>>> np.Inf    #正无穷大
inf
>>> np.NAN    #非数字
nan
>>> np.Infinity
inf
>>> np.MAXDIMS
32
>>> np.NINF    #负无穷大
-inf
>>> np.NaN
nan
>>> np.NZERO    #负0
-0.0

9.矩阵在不同维度上的计算

>>> x=np.matrix(np.arange(0,10).reshape(2,5))    #二维矩阵
>>> x
matrix([[0, 1, 2, 3, 4],
        [5, 6, 7, 8, 9]])
>>> x.sum()    #所有元素之和
45
>>> x.sum(axis=0)    #纵向求和
matrix([[ 5,  7,  9, 11, 13]])
>>> x.sum(axis=1)    #横向求和
matrix([[10],
        [35]])
>>> x.mean()    #平均值
4.5
>>> x.mean(axis=1)
matrix([[2.],
        [7.]])
>>> x.mean(axis=0)
matrix([[2.5, 3.5, 4.5, 5.5, 6.5]])
>>> weight=[0.3,0.7]    #权重
>>> np.average(x,axis=0,weights=weight)
matrix([[3.5, 4.5, 5.5, 6.5, 7.5]])
>>> x.max()    #所有元素最大值
9
>>> x.max(axis=0)    #纵向最大值
matrix([[5, 6, 7, 8, 9]])
>>> x.max(axis=1)    #横向最大值
matrix([[4],
        [9]])
>>> x=np.matrix(np.random.randint(0,10,size=(3,3)))
>>> x
matrix([[3, 7, 7],
        [7, 0, 9],
        [4, 0, 8]])
>>> x.std()    #标准差
3.197221015541813
>>> x.std(axis=1)    #横向标准差
matrix([[1.88561808],
        [3.8586123 ],
        [3.26598632]])
>>> x.std(axis=0)    #纵向标准差
matrix([[1.69967317, 3.29983165, 0.81649658]])
>>> x.var(axis=0)    #纵向方差
matrix([[ 2.88888889, 10.88888889,  0.66666667]])
>>> x.sort(axis=0)    #纵向排序
>>> x
matrix([[3, 0, 7],
        [4, 0, 8],
        [7, 7, 9]])
>>> x.sort(axis=1)    #横向排序
>>> x
matrix([[0, 3, 7],
        [0, 4, 8],
        [7, 7, 9]])

10.应用

（1）使用蒙特·卡罗方法估计圆周率的值

>>> def numpyPI(times):
...     x=np.random.rand(times)
...     y=np.random.rand(times)
...     hits=np.sum(x**2+y**2<=1)
...     pi=hits/times*4
...     return pi
... 
>>> numpyPI(1000000)
3.143172

（2）复利计算公式

>>> import numpy_financial as npf
>>> round(npf.fv(0.05,39,-14000,-14000))#每年固定存入14000元，年利率固定为5%，40年后的余额
1691197

三、计算特征值与正特征向量

对于n*n方阵A，如果存在标量λ和n维非0向量x，使得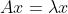成立，哪个称λ是方阵A的一个特征值，x为对应λ的特征向量
从几何意义来讲，矩阵乘以一个向量，是对这个向量进行了一个变换，从一个坐标系变换到另一个坐标系。在变换过程中，向量主要发生旋转和缩放这两种变化。如果矩阵乘以一个向量之后，向量只发生了缩放变化而没有进行旋转，那么这个向量就是该矩阵的特征向量，缩放的比例就是特征值。或者说，特征向量是对数据进行旋转之后理想的坐标轴之一，而特征值则是该坐标轴上的投影或者贡献。特征值越大，表示这个坐标轴对原向量的表达越重要，原向量在这个个坐标轴上的投影越大。一个矩阵的所有特征向量组成了该矩阵的一组基，也就是新坐标中的轴。有个特征值和特征向量之后，向量就可以在另一个坐标系中进行表示。

>>> A=np.array([[1,-3,3],[3,-5,3],[6,-6,4]])
>>> print(A)
[[ 1 -3  3]
 [ 3 -5  3]
 [ 6 -6  4]]
>>> e,v=np.linalg.eig(A)    #特征值与特征向量
>>> print(e)
[ 4.+0.00000000e+00j -2.+1.10465796e-15j -2.-1.10465796e-15j]
>>> print(v)
[[-0.40824829+0.j          0.24400118-0.40702229j  0.24400118+0.40702229j]
 [-0.40824829+0.j         -0.41621909-0.40702229j -0.41621909+0.40702229j]
 [-0.81649658+0.j         -0.66022027+0.j         -0.66022027-0.j        ]]
>>> print(np.linalg.eig)
<function eig at 0x0000027435CD67A0>
>>> print(np.linalg.eigvals(A))
[ 4.+0.00000000e+00j -2.+1.10465796e-15j -2.-1.10465796e-15j]
>>> print(e*v)    #特征值与特征向量的乘积
[[-1.63299316+0.00000000e+00j -0.48800237+8.14044580e-01j
  -0.48800237-8.14044580e-01j]
 [-1.63299316+0.00000000e+00j  0.83243817+8.14044580e-01j
   0.83243817-8.14044580e-01j]
 [-3.26598632+0.00000000e+00j  1.32044054-7.29317578e-16j
   1.32044054+7.29317578e-16j]]
>>> print(np.isclose(np.dot(A,v),e*v))    #检验二者是否相等
[[ True  True  True]
 [ True  True  True]
 [ True  True  True]]
>>> print(np.linalg.det(A-np.eye(3,3)*e))    #行列式|A-λE|的值应为0
5.965152994198125e-14j

四、计算逆矩阵

>>> x=np.matrix([[1,2,3],[4,5,6],[7,8,0]])
>>> y=np.linalg.inv(x)    #计算x逆矩阵
>>> print(y)
[[-1.77777778  0.88888889 -0.11111111]
 [ 1.55555556 -0.77777778  0.22222222]
 [-0.11111111  0.22222222 -0.11111111]]
>>> print(x*y)    #对角元素为1，其他元素为0或者近似为0
[[ 1.00000000e+00  5.55111512e-17  1.38777878e-17]
 [ 5.55111512e-17  1.00000000e+00  2.77555756e-17]
 [ 1.77635684e-15 -8.88178420e-16  1.00000000e+00]]
>>> print(np.round(y*x))
[[ 1. -0.  0.]
 [ 0.  1.  0.]
 [ 0.  0.  1.]]

五、求解线性方程组

线性方程组

>>> a=np.array([[3,1],[1,2]])    #系数矩阵
>>> b=np.array([9,8])    
>>> x=np.linalg.solve(a,b)    #求解
>>> print(x)
[2. 3.]
>>> print(np.dot(a,x))    #验证
[9. 8.]
>>> print(np.linalg.lstsq(a,b))    #最小二乘解（返回解、余项、a的秩、a的奇异值）

Warning (from warnings module):
  File "<pyshell#81>", line 1
FutureWarning: `rcond` parameter will change to the default of machine precision times ``max(M, N)`` where M and N are the input matrix dimensions.
To use the future default and silence this warning we advise to pass `rcond=None`, to keep using the old, explicitly pass `rcond=-1`.
(array([2., 3.]), array([], dtype=float64), 2, array([3.61803399, 1.38196601]))
>>> print(np.linalg.matrix_rank(a))    #a的秩
2
>>> U,sv,V=np.linalg.svd(a,full_matrices=False)    #奇异值分解
>>> print(sv)    #a的奇异值
[3.61803399 1.38196601]
>>> print(U)
[[-0.85065081 -0.52573111]
 [-0.52573111  0.85065081]]
>>> print(V)
[[-0.85065081 -0.52573111]
 [-0.52573111  0.85065081]]

六、计算向量和矩阵的范数

>>> x=np.matrix([[1,2],[3,-4]])
>>> np.linalg.norm(x)    #F范数=(1**2+2**2+3**2+(-4)**2)**0.5
5.477225575051661
>>> np.linalg.norm(x,-2)    #smallest singular value
1.9543950758485487
>>> np.linalg.norm(x,-1)    #min(sum(abs(x),axis=0))
4.0
>>> np.linalg.norm(x,1)    #max(sum(abs(x),axis=0))
6.0
>>> np.linalg.norm(np.array([1,2,3,4]),3)
4.641588833612778

七、计算矩阵的幂，矩阵自乘

>>> np.linalg.matrix_power([[1,2],[3,4]],2)    #自乘2次
array([[ 7, 10],
       [15, 22]])
>>> np.linalg.matrix_power([[1,2],[3,4]],5)    #自乘5次
array([[1069, 1558],
       [2337, 3406]])
>>> x=np.matrix([[1,2],[3,4]])
>>> x**2    #也可以直接使用运算符**
matrix([[ 7, 10],
        [15, 22]])
>>> x**5
matrix([[1069, 1558],
        [2337, 3406]])

八、矩阵奇异值分解

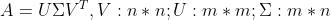
其中，A,U都是正交阵，Σ是对角阵

>>> a=np.arange(60).reshape(5,-1)
>>> a
array([[ 0,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11],
       [12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23],
       [24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35],
       [36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47],
       [48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59]])
>>> U,s,V=np.linalg.svd(a,full_matrices=False)
>>> np.dot(U,np.dot(np.diag(s),V))
array([[2.32096525e-15, 1.00000000e+00, 2.00000000e+00, 3.00000000e+00,
        4.00000000e+00, 5.00000000e+00, 6.00000000e+00, 7.00000000e+00,
        8.00000000e+00, 9.00000000e+00, 1.00000000e+01, 1.10000000e+01],
       [1.20000000e+01, 1.30000000e+01, 1.40000000e+01, 1.50000000e+01,
        1.60000000e+01, 1.70000000e+01, 1.80000000e+01, 1.90000000e+01,
        2.00000000e+01, 2.10000000e+01, 2.20000000e+01, 2.30000000e+01],
       [2.40000000e+01, 2.50000000e+01, 2.60000000e+01, 2.70000000e+01,
        2.80000000e+01, 2.90000000e+01, 3.00000000e+01, 3.10000000e+01,
        3.20000000e+01, 3.30000000e+01, 3.40000000e+01, 3.50000000e+01],
       [3.60000000e+01, 3.70000000e+01, 3.80000000e+01, 3.90000000e+01,
        4.00000000e+01, 4.10000000e+01, 4.20000000e+01, 4.30000000e+01,
        4.40000000e+01, 4.50000000e+01, 4.60000000e+01, 4.70000000e+01],
       [4.80000000e+01, 4.90000000e+01, 5.00000000e+01, 5.10000000e+01,
        5.20000000e+01, 5.30000000e+01, 5.40000000e+01, 5.50000000e+01,
        5.60000000e+01, 5.70000000e+01, 5.80000000e+01, 5.90000000e+01]])
>>> np.allclose(a,np.dot(U,np.dot(np.diag(s),V)))
True

九、计算数组或矩阵的行列式

>>> a=[[1,2],[3,4]]
>>> np.linalg.det(a)
-2.0000000000000004
>>> a=np.array([[[1,2],[3,4]],[[1,2],[2,1]],[[1,3],[3,1]]])
>>> np.linalg.det(a)
array([-2., -3., -8.])

十、矩阵QR分解

如果实（复）非奇异矩阵A能够化成正交（酉）矩阵Q与实（复）非奇异上三角矩阵R的乘积，即A=QR，则称其为A的QR分解

>>> a=np.matrix([[1,2,3],[4,5,6]])
>>> q,r=np.linalg.qr(a)
>>> print(q,r,sep='\\n\\n')
[[-0.24253563 -0.9701425 ]
 [-0.9701425   0.24253563]]

[[-4.12310563 -5.33578375 -6.54846188]
 [ 0.         -0.72760688 -1.45521375]]
>>> np.dot(1,r)
matrix([[-4.12310563, -5.33578375, -6.54846188],
        [ 0.        , -0.72760688, -1.45521375]])

十一、读写文件

numpy文件读写主要有二进制的文件读写和文件列表形式的数据读写两种形式

save函数是以二进制的格式保存数据。

np.save("../tmp/save_arr",arr)

load函数是从二进制的文件中读取数据

np.load("../tmp/save_arr.npy")

savez函数可以将多个数组保存到一个文件中

np.savez('../tmp/savez_arr',arr1,arr2)

存储时可以省略扩展名，但读取时不能省略扩展名

读取文本格式的数据

savetxt函数是将数组写到某种分隔符隔开的文本文件中

np.savetxt("../tmp/arr.txt",arr,fmt="%d",delimiter=",")

loadtxt函数执行的是把文件加载到一个二维数组中

np.loadtxt("../tmp/arr.txt",delimiter=",")

genfromtxt函数面向的是结构化数组和缺失数据

np.genfromtxt("../tmp/arr.txt",delimiter=",")

>>> x=np.random.rand(4,10)
>>> np.save('data.npy',x)
>>> y=np.load('data.npy')
>>> y
array([[0.41902235, 0.69427069, 0.37598648, 0.73763434, 0.37021849,
        0.22994088, 0.89334764, 0.04995869, 0.18538797, 0.84465261],
       [0.97907058, 0.27427357, 0.11774563, 0.90859496, 0.86412135,
        0.643867  , 0.09459659, 0.1766268 , 0.2050061 , 0.82050625],
       [0.89201862, 0.64940355, 0.50761076, 0.79521352, 0.52232466,
        0.85287866, 0.91648536, 0.75976614, 0.2113207 , 0.07295113],
       [0.41439073, 0.07900488, 0.52060863, 0.92372387, 0.88509664,
        0.50123086, 0.8048252 , 0.38571732, 0.01780673, 0.87969947]])
>>> x=np.matrix([[1,2,3],[4,5,6]])
>>> x
matrix([[1, 2, 3],
        [4, 5, 6]])
>>> np.savetxt('x.txt',x)
>>> np.loadtxt('x.txt')
array([[1., 2., 3.],
       [4., 5., 6.]])
>>> with open('x.txt') as fp:
...     print(fp.read())
... 
...     
1.000000000000000000e+00 2.000000000000000000e+00 3.000000000000000000e+00
4.000000000000000000e+00 5.000000000000000000e+00 6.000000000000000000e+00
>>> a_mat=np.matrix([3,5,7])
>>> a_mat.tostring()
Warning (from warnings module):
  File "<pyshell#126>", line 1
DeprecationWarning: tostring() is deprecated. Use tobytes() instead.
b'\\x03\\x00\\x00\\x00\\x05\\x00\\x00\\x00\\x07\\x00\\x00\\x00'
>>> a_mat.dumps()    #dumps()方法用于将数据进行序列化
b'\\x80\\x02cnumpy.core.multiarray\\n_reconstruct\\nq\\x00cnumpy\\nmatrix\\nq\\x01K\\x00\\x85q\\x02c_codecs\\nencode\\nq\\x03X\\x01\\x00\\x00\\x00bq\\x04X\\x06\\x00\\x00\\x00latin1q\\x05\\x86q\\x06Rq\\x07\\x87q\\x08Rq\\t(K\\x01K\\x01K\\x03\\x86q\\ncnumpy\\ndtype\\nq\\x0bX\\x02\\x00\\x00\\x00i4q\\x0c\\x89\\x88\\x87q\\rRq\\x0e(K\\x03X\\x01\\x00\\x00\\x00<q\\x0fNNNJ\\xff\\xff\\xff\\xffJ\\xff\\xff\\xff\\xffK\\x00tq\\x10b\\x89h\\x03X\\x0c\\x00\\x00\\x00\\x03\\x00\\x00\\x00\\x05\\x00\\x00\\x00\\x07\\x00\\x00\\x00q\\x11h\\x05\\x86q\\x12Rq\\x13tq\\x14b.'
>>> np.loads(_)    #loads()方法用于反序列化，还原为原来的信息
Traceback (most recent call last):
  File "<pyshell#128>", line 1, in <module>
    np.loads(_)
  File "E:\\python 3.7\\lib\\site-packages\\numpy\\__init__.py", line 311, in __getattr__
    raise AttributeError("module !r has no attribute "
AttributeError: module 'numpy' has no attribute 'loads'. Did you mean: 'load'?
>>> a_mat.dump('x.dat')                      
>>> np.load('x.dat')
Traceback (most recent call last):
  File "<pyshell#133>", line 1, in <module>
    np.load('x.dat')
  File "E:\\python 3.7\\lib\\site-packages\\numpy\\lib\\npyio.py", line 418, in load
    raise ValueError("Cannot load file containing pickled data "
ValueError: Cannot load file containing pickled data when allow_pickle=False

以上是关于如何计算一个矩阵的幂的主要内容，如果未能解决你的问题，请参考以下文章