LSGAN:最小二乘生成对抗网络

Posted 2023-04-05

参考技术A

解决问题： 解决传统 GAN 生成图片质量不高，训练不稳定的问题。

做法： 将传统 GAN 的 交叉熵损失函数 换成 最小二乘损失函数

本篇主要通过GAN对比来学习LSGAN

通过例子介绍：

使用 位于决策边界正确侧 但仍然 远离真实数据的假样本 更新生成器时，交叉熵损失函数将导致梯度消失的问题。
如图 (b)所示，当我们使用 假样本 (品红色)通过使鉴别器相信它们来自真实数据来更新生成器时，它 几乎不会引起错误 ，因为它们在正确的一侧，既决策边界的真实数据面。
然而，这些样本 仍然离真实数据很远 ，我们想把它们拉得接近真实数据。

问题总结：在交叉熵损失函数情况下，判别器判定真实面的假数据距离真实数据较远，效果不足。

基于这一观察，我们提出了最小二乘生成对抗网络，它采用 最小二乘损失函数作为鉴别器 。
最小二乘损失函数能够 将伪样本移向决策边界 ，
因为最小二乘损失函数会 惩罚位于决策边界正确一侧很远的样本 。
如图 (c)所示，最小二乘损失函数将惩罚假样本(品红色)，并 将它们拉向决策边界 ，使它们被正确分类。

基于这一特性，最小二乘能够生成更接近真实数据的样本

总结概括
最小二乘： 最小二乘损失与交叉熵损失相比，优势在于生成样本在欺骗判别器的前提下同时让生成器把 距离决策边界比较远 的生成图片拉向 决策边界 ，这样保证了生成高质量的样本。

交叉熵： 以交叉熵作为损失，会使得生成器 不会再优化那些被判别器识别为真实图片的生成图片 ，即使这些生成图片距离判别器的决策边界仍然很远，也就是距离真实数据比较远，因为此时的交叉熵损失已经很小，生成器完成了为它设计的目标。

LSGAN的缺陷： 在于它并 没有解决当判别器足够优秀时生成器发生梯度弥散的问题

梯度弥散: 使用反向传播算法传播梯度的时候，随着传播深度的增加， 梯度的幅度会急剧减小，会导致浅层神经元的权重更新非常缓慢 ，不能有效学习。
这样一来，深层模型也就变成了前几层相对固定，只能改变最后几层的浅层模型。

GANs 的损失函数：

LSGANs的损失函数：
最小二乘

公式注释：
鉴别器 D
生成器 G
G 的目标是学习数据 x 上的分布 pg。
G 服从均匀或高斯分布 pz(z)对输入变量 z 进行采样开始，然后将输入变量 z 映射到数据空间 G(z； θg)。
D 是分类器 D(x； θd)，其目的是识别图像是来自训练数据还是来自g。
z 为噪音，它可以服从归一化或者高斯分布，为真实数据 x 服从的概率分布，为 z 服从的概率分布。为期望值，同为期望值。

假设我们对鉴别器使用 a-b 编码方案 ，其中a 和b 分别是假数据和真实数据的标签。

c 表示 G 预测的D 相信的假数据的值。

最小二乘法的具体优点：
1.决策边界固定（鉴别器参数固定），生成样本靠近决策边界，更接近真实数据。
2.惩罚远离决策边界的样本时，可以在更新生成器时生成更多的梯度，这反过来缓解了梯度消失的问题（梯度消失：前面隐藏层的学习速率低于后面隐藏层的学习速率，即随着隐藏层数目的增加，分类准确率反而下降）

GAN中：最小化等式 1 产生最小化詹森-香农散度:

LSGAN：探讨LSGAN与f散度的关系

公式解释：（下文关于a-b编码证明a,b,c条件）
将

加入到

并不会改变最佳值，因为并没有引入含有G的参数

从而我们可以推出G固定情况下的最佳鉴别器：

使用 pd 来表示 pdata，来重新表示4式

此处不详细证明
化简为：

如果： b-c = 1， b-a = 2，则

是皮尔逊散度，总之可证，当 a,b,c满足b-c = 1 和 b-a = 2的条件，则最小化等式 4 会使 pd + pg 和 2pg 之间的皮尔逊 χ2 散度最小化。

采用 a-b编码方案：

由上述证明可设a = 1， b = 1， c = 0

采用 0-1二进制编码方案 ：

两式接近，但此处，论文作者采用a-b编码方式，来实现实验：

带上其中一个实验：

参考论文：Mao X D, Li Q, Xie H R, et al. Least squares generative
adversarial networks[C]//Proceedings of the 2017 IEEE
International Conference on Computer Vision, Venice, Oct
22- 29, 2017. Washington: IEEE Computer Society, 2017:
2813-2821.

GAN Step By Step -- Step6 LSGAN

GAN Step By Step

心血来潮

GSBS，顾名思义，我希望我自己能够一步一步的学习GAN。GAN 又名 生成对抗网络，是最近几年很热门的一种无监督算法，他能生成出非常逼真的照片，图像甚至视频。GAN是一个图像的全新的领域，从2014的GAN的发展现在，在计算机视觉中扮演这越来越重要的角色，并且到每年都能产出各色各样的东西，GAN的理论和发展都蛮多的。我感觉最近有很多人都在学习GAN，但是国内可能缺少比较多的GAN的理论及其实现，所以我也想着和大家一起学习，并且提供主流框架下 pytorch,tensorflow,keras 的一些实现教学。

在一个2016年的研讨会，杨立昆描述生成式对抗网络是“机器学习这二十年来最酷的想法”。

---

Step6 LSGAN (Least Squares GAN)

Least Squares GAN

Least Squares Generative Adversarial Networks

Authors

Xudong Mao, Qing Li, Haoran Xie, Raymond Y.K. Lau, Zhen Wang, Stephen Paul Smolley

Abstract

Unsupervised learning with generative adversarial networks (GANs) has proven hugely successful. Regular GANs hypothesize the discriminator as a classifier with the sigmoid cross entropy loss function. However, we found that this loss function may lead to the vanishing gradients problem during the learning process. To overcome such a problem, we propose in this paper the Least Squares Generative Adversarial Networks (LSGANs) which adopt the least squares loss function for the discriminator. We show that minimizing the objective function of LSGAN yields minimizing the Pearson χ2 divergence. There are two benefits of LSGANs over regular GANs. First, LSGANs are able to generate higher quality images than regular GANs. Second, LSGANs perform more stable during the learning process. We evaluate LSGANs on five scene datasets and the experimental results show that the images generated by LSGANs are of better quality than the ones generated by regular GANs. We also conduct two comparison experiments between LSGANs and regular GANs to illustrate the stability of LSGANs.

[Paper] [Code]

近几年来 GAN 是十分火热的，由 Goodfellow 在 14 年发表论文 Generative Adversarial Nets 开山之作以来，生成式对抗网络一直都备受机器学习领域的关注，这种两人零和博弈的思想十分有趣，充分体现了数学的美感。从 GAN 到 WGAN的优化，再到本文介绍的 LSGANs，再到还有很火的 BigGAN ，可以说生成式对抗网络的魅力无穷，而且它的用处也是非常奇妙，如今还被用在例如无负样本的情况下如何训练分类器，例如 AnoGAN等等

LSGANs 这篇经典的论文主要工作是把交叉熵损失函数换做了最小二乘损失函数，这样做作者认为改善了传统 GAN 的两个问题，即传统 GAN 生成的图片质量不高，而且训练过程十分不稳定。

LSGANs 试图使用不同的距离度量来构建一个更加稳定而且收敛更快的，生成质量高的对抗网络。

LSGAN的损失函数

Least Squares GAN 比最原始的 GANs 的 loss 更加稳定，通过名字我们也能够看出这种 GAN 是通过最小平方误差来进行估计，而不是通过二分类的损失函数，下面我们看看 loss 的计算公式
$${\ell }_G=\frac{1}{2}{\mathbb{E}}_{z\sim p(z)}\left[{\left(D(G(z))-1\right)}^2\right]$$

$${\ell }_D=\frac{1}{2}{\mathbb{E}}_{x\sim p_{\text{data}}}\left[{\left(D(x)-1\right)}^2\right]+\frac{1}{2}{\mathbb{E}}_{z\sim p(z)}\left[{\left(D(G(z))\right)}^2\right]$$

LSGAN两种模型架构和训练

模型的结构

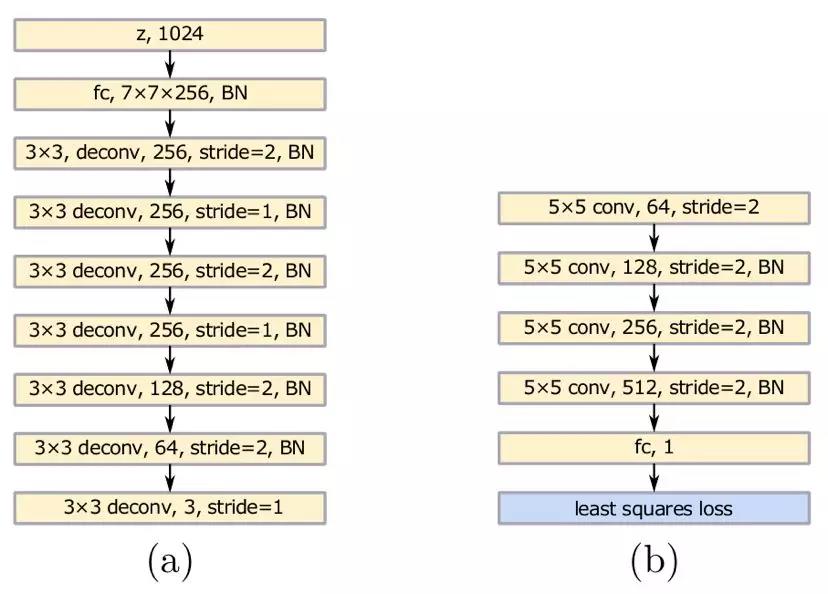
作者也提出了两类架构：

第一种处理类别少的情况，例如 MNIST、LSUN。网络设计如下：

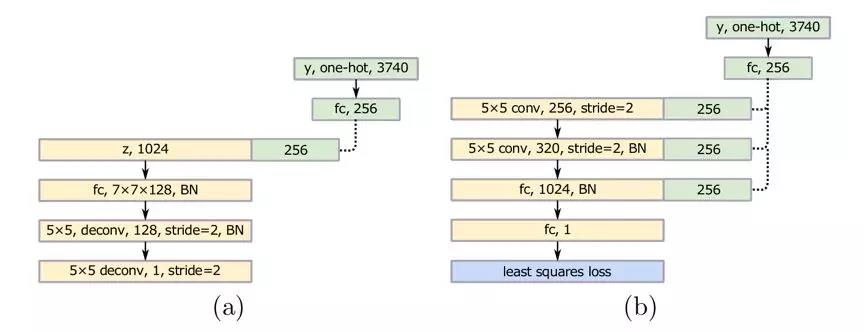
第二类处理类别特别多的情形，实际上是个条件版本的 LSGAN。针对手写汉字数据集，有 3740 类，提出的网络结构如下：

传统GANs和LSGANs的比较

论文中使用了很多场景的数据集，然后比较了传统 GANs 和 LSGANs 的稳定性，最后还通过训练 3740 个类别的手写汉字数据集来评价 LSGANs。

▲ 本文使用的数据集列表

在 LSUN 和 HWDB1.0 的这两个数据集上使用 LSGANs 的效果图如下，其中 LSUN 使用了里面的 bedroom, kitchen, church, dining room 和 conference room 五个场景，bedroom 场景还对比了 DCGANs 和 EBGANs 的效果在图 5 中，可以观察到 LSGANs 生成的效果要比那两种的效果好。

图 7 则体现了 LSGANs 和传统 GANs 生成的图片对比

通过实验观察，作者发现 4 点技巧：

\\1. 生成器 G 带有 batch normalization 批处理标准化（以下简称 BN）并且使用 Adam 优化器的话，LSGANs 生成的图片质量好，但是传统 GANs 从来没有成功学习到，会出现 mode collapse 现象；

\\2. 生成器 G 和判别器 D 都带有 BN 层，并且使用 RMSProp 优化器处理，LSGANs 会生成质量比 GANs 高的图片，并且 GANs 会出现轻微的 mode collapse 现象；

\\3. 生成器 G 带有 BN 层并且使用 RMSProp 优化器，生成器 G 判别器 D 都带有 BN 层并且使用 Adam 优化器时，LSGANs 与传统 GANs 有着相似的表现；

\\4. RMSProp 的表现比 Adam 要稳定，因为传统 GANs 在 G 带有 BN 层时，使用 RMSProp 优化可以成功学习，但是使用 Adam 优化却不行。

下面是使用 LSGANs 和 GANs 学习混合高斯分布的数据集，下图展现了生成数据分布的动态结果，可以看到传统 GAN 在 Step 15k 时就会发生 mode collapse 现象，但 LSGANs 非常成功地学习到了混合高斯分布。

MNIST数据集测试

下面没有给出所有的代码，因为大致是一样的，只是变化了损失函数

在上面可以看到 Least Squares GAN 通过最小二乘代替了二分类的 loss，下面我们定义一下 loss 函数

def ls_discriminator_loss(scores_real, scores_fake):
    loss = 0.5 * ((scores_real - 1) ** 2).mean() + 0.5 * (scores_fake ** 2).mean()
    return loss

def ls_generator_loss(scores_fake):
    loss = 0.5 * ((scores_fake - 1) ** 2).mean()
    return loss

这里定义判别器和损失函数，然后进行训练即可

D = discriminator().cuda()
G = generator().cuda()

D_optim = get_optimizer(D)
G_optim = get_optimizer(G)

train_a_gan(D, G, D_optim, G_optim, ls_discriminator_loss, ls_generator_loss)

Iter: 0, D: 0.5524, G:0.4728

Iter: 250, D: 0.2155, G:0.1959

…

Iter: 3500, D: 0.1186, G:0.3989

Iter: 3750, D: 0.1621, G:0.228

比较实验结果

这里面也大概给个数据进行比较

LSGANs：

GAN：

从本次用 MNIST 数据训练的效果来看，LSGANs 生成的效果似乎是比 GAN 的要清晰高质量一些。

总结

LSGANs 是对 GAN 的一次优化，从实验的情况中，有时候也发现了一些奇怪的现象。我本来是参考论文把判别器 D 的损失值，按真假两种 loss 加起来一并放入 Adam 中优化，但是无论如何都学习不成功，梯度还是弥散了，最后把 D_fake_loss 和 D_real_loss 分为两个 program，放入不同的 Adam 中优化判别器D 的参数才达到预期效果。

这篇论文中的思想是非常值得借鉴的，从最小二乘的距离的角度考量，并不是判别器分类之后就完事了，但是 LSGANs 其实还是未能解决判别器足够优秀的时候，生成器梯度弥散的问题。