夜深人静写算法- 搜索入门

Posted 2023-01-17 英雄哪里出来

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了夜深人静写算法- 搜索入门相关的知识，希望对你有一定的参考价值。

文章目录

一、前言
二、搜索算法的原理
三、深度优先搜索
四、广度优先搜索
- 1、BFS
五、搜索题集整理

一、前言

目前本专栏正在进行优惠活动，在博主主页添加博主好友，可以获取 付费专栏优惠券。
回首往事，再来看自己五年前写的这篇文章《夜深人静写算法（一）- 搜索入门》，发现虽然标题写的是入门，但是还是有很多地方较为晦涩，而且多为文字，图片相对较少，初学者不易理解，这和我当初分享算法的初衷背道而驰。毕竟我不希望很多壮怀激烈的仁人志士因为我的文章放弃了算法这条路。
因为，我的愿景是：让天下没有难学的算法。
基于这个原因，我打算重新整理《夜深人静写算法》系列，让同样和我志同道合的人积极投身到这个事业中来，将祖国的算法和技术发扬光大，背靠祖国，面向国际，强我国威，壮我河山！
这次的修订版本会持续连载，并且会从易到难重新整理规划目录，读者可以放心从前往后阅读，如果中途有涉及到一些数学、数据结构、计算机原理方面的知识，我会另外开辟章节进行详细讲解。当然，如果有遇到写的不清楚的地方，也可以给我留言，我会尽我最大的努力把它调整清晰，文章群体主要面向中小学生以及大学生，毕竟，你们才是国家未来的栋梁之才！

二、搜索算法的原理

搜索算法的原理就是枚举。利用计算机的高性能，给出人类制定好的规则，枚举出所有可行的情况，找到可行解或者最优解。
比较常见的搜索算法是深度优先搜索（又叫深度优先遍历）和广度优先搜索（又叫广度优先遍历或者宽度优先遍历）。各种图论的算法基本都是依靠这两者进行展开的。
深度优先搜索一般用来求可行解，利用剪枝进行优化，在树形结构的图上用处较多；而广度优先搜索一般用来求最优解，配合哈希表进行状态空间的标记，从而避免重复状态的计算；

三、深度优先搜索

1、DFS

1）算法原理

深度优先搜索（Depth First Search），是图遍历算法的一种。用一句话概括就是：“一直往下走，走不通回头，换条路再走，直到无路可走”。具体算法描述为：

选择一个起始点 $u$ 作为 当前结点，执行如下操作：
a. 访问当前结点，并且标记该结点已被访问，然后跳转到 b；
b. 如果存在一个和当前结点相邻并且尚未被访问的结点 v，则将 v 设为当前结点，继续执行 a；
c. 如果不存在这样的 v，则进行回溯，回溯的过程就是回退当前结点；

上述所说的 当前结点 需要用一个栈来维护，每次访问到的结点入栈，回溯的时候出栈（栈是数据结构中线性表的一种，我会另外开辟一个章节来仔细讲解栈的原理和应用）。
除了栈，另一种实现深度优先搜索的方式是递归，代码更加简单，相对好理解；

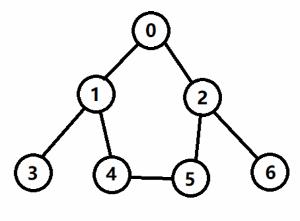
【例题1】给定一个 n 个结点的无向图，要求从 0 号结点出发遍历整个图，求输出整个过程的遍历序列。其中，遍历规则为：
1）如果和当前结点相邻的结点已经访问过，则不能再访问；
2）每次从和当前结点相邻的结点中寻找一个编号最小的没有访问的结点进行访问；

图三-1

如图1所示，对上图以深度优先的方式进行遍历，起点是 0；
<1> 第一步，当前结点为 0，标记已访问，然后从相邻结点中找到编号最小的且没有访问的结点 1；
<2> 第二步，当前结点为 1，标记已访问，然后从相邻结点中找到编号最小的且没有访问的结点 3；
<3> 第三步，当前结点为 3，标记已访问，没有尚未访问的相邻结点，执行回溯，回到结点 1；
<4> 第四步，当前结点为 1，从相邻结点中找到编号最小的且没有访问的结点 4；
<5> 第五步，当前结点为 4，标记已访问，然后从相邻结点中找到编号最小的且没有访问的结点 5；
<6> 第六步，当前结点为 5，标记已访问，然后从相邻结点中找到编号最小的且没有访问的结点 2；
<7> 第七步，当前结点为 2，标记已访问，然后从相邻结点中找到编号最小的且没有访问的结点 6；
<8> 第八步，当前结点为 6，标记已访问，没有尚未访问的相邻结点，执行回溯，回到结点 2；
<9> 第九步，按照 2 => 5 => 4 => 1 => 0 的顺序一路回溯，搜索结束；

图三-2

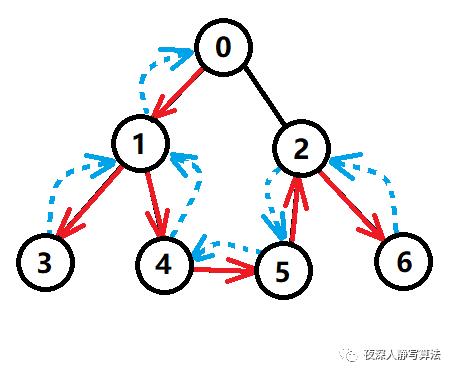
如图三-2 所示，红色实箭头表示搜索路径，蓝色虚箭头表示回溯路径。

图三-2-1

- 图三-2-1中，红色块表示往下搜索，蓝色块表示往上回溯，遍历序列为：

	0 -> 1 -> 3 -> 4 -> 5 -> 2 -> 6

2）算法实现

const int MAXN = 7;

void dfs(int u) 
    if(visit[u])                                 // 1
        return ;
    
    visit[u] = true;                              // 2
    dfs_add(u);                                   // 3
    for(int i = 0; i < MAXN; ++i) 
        int v = i;
        if(adj[u][v])                            // 4
            dfs(v);                               // 5

1、visit[MAXN]数组是一个bool数组，用于标记某个节点是否已访问，初始化都为 false；这里对已访问结点执行回溯；
2、visit[u] = true;对未访问结点 u 标记为已访问状态；
3、dfs_add(u);用来将 u 存储到的访问序列中，实际函数实现如下：

void dfs_add(int u) 
    ans[ansSize++] = u;

4、adj[MAXN][MAXN]是图的邻接矩阵，用 0 或 1 来代表点是否连通，对于上面的例子，邻接矩阵表示如下：

bool adj[MAXN][MAXN] = 
    0, 1, 1, 0, 0, 0, 0,
    1, 0, 0, 1, 1, 0, 0,
    1, 0, 0, 0, 0, 1, 1,
    0, 1, 0, 0, 0, 0, 0,
    0, 1, 0, 0, 0, 1, 0,
    0, 0, 1, 0, 1, 0, 0,
    0, 0, 1, 0, 0, 0, 0,
;

（adj[u][v] = 1代表 u 和 v 之间有一条有向边；adj[u][v] = 0代表没有边）

5、递归调用相邻结点；

3）基础应用

a. 求阶乘

【例题2】给出 $\\le 10 )$ ，求 $n! = n * (n - 1) * . . . * 3 * 2 * 1$ ；

令 $f (n) = n!$ ，那么有 $f (n) = n * f (n - 1)$ $(n > 0)$ 。由于满足递归的性质，可以认为这是一个 $n + 1$ 个结点的图，结点 $\\ge 1)$ 到结点 $i - 1$ 有一条权值为 $i$ 的有向边，从 $n$ 开始进行深度优先搜索，搜索的终点是结点 $0$ ，返回值为 1 (即 $0! = 1$ )。

图三-3

如图三-3所示， $n!$ 的递归计算看成是一个深度优先搜索的过程，红色路径代表递归往下搜索，蓝色路径代表回溯，并且每次回溯的时候会将遍历的结果返回给上一个结点（当然，这只是一个思想，并不代表这是求 $n!$ 的高效算法）。
C++ 代码实现如下：

int dfs(int n) 
    return !n ? 1 : n * dfs(n-1);

(由于 C++ 中的 int 是 32 位整数，最大能够表示的值为 $2^32-1$ ，所以这里的 n 太大就会导致溢出，需要用数组来模拟实现高精度，这个也会在后面的章节来详细讲解如何实现一个高精度的四则运算)

b. 求斐波那契数列的第n项

【例题3】令 $g (n) = g (n - 1) + g (n - 2)$ ， $(1 < n < 40)$ ，其中 $g (0) = g (1) = 1$ ；

同样可以利用图论的思想，从结点 $n$ 向 $n - 1$ 和 $n - 2$ 分别引一条权值为1的有向边，每次求 $g (n)$ 就是以 $n$ 作为起点，对 $n$ 进行深度优先搜索，然后将 $n - 1$ 和 $n - 2$ 回溯的结果相加作为 $n$ 结点的值，即 $g (n)$ 。

图三-4

C++ 代码实现如下：

int dfs(unsigned int n) 
    if(n <= 1) 
        return 1;
    
    return dfs(n-1) + dfs(n-2);

例如， $g (5)$ 的计算流程如图三-4-1所示：

图三-4-1

这里会带来一个问题， $g (n)$ 的计算需要用到 $g (n - 1)$ 和 $g (n - 2)$ ，而 $g (n - 1)$ 的计算需要用到 $g (n - 2)$ 和 $g (n - 3)$ ，所以我们发现 $g (n - 2)$ 被用到了两次，而且每个结点都存在这个问题，这样就使得整个算法的时间复杂度变成指数级了，对于斐波那契数列递归算法的时间复杂度分析，可以参考这篇文章：斐波那契数列递归时间复杂度分析
为了规避这个问题，下面会讲到基于深搜的记忆化搜索。

c. 求 n 个数的全排列

【例题4】给定 $n$ ，按字典序输出 1 到 $n$ 的所有全排列；

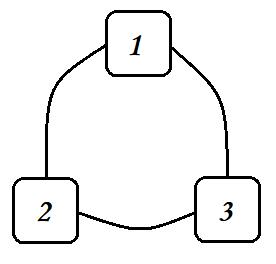
全排列的种数是 $n!$ ，要求按照字典序输出。这是最典型的深搜问题。我们可以把 $n$ 个数两两建立无向边（即任意两个结点之间都有边，也就是一个 $n$ 个结点的完全图），然后对每个点作为起点，分别做一次深度优先搜索，当所有点都已经标记时，输出当前的搜索路径，就是其中一个排列；
这里需要注意的是，回溯的时候需要将原先标记的点的标记取消，否则只能输出一个排列。如果要按照字典序，则需要在遍历的时候保证每次遍历都是按照结点从小到大的方式进行遍历的。

图三-5

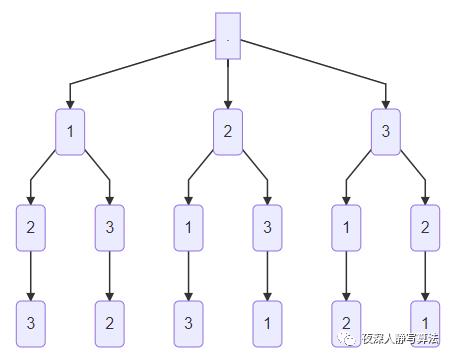
如图三-6所示，代表了一个 3个数的全排列的深度优先搜索空间树；

图三-6

C++ 代码实现如下：

void dfs(int depth)                                   // 1
    if(depth == MAXN)                                 // 2
        dfs_print();
        return;
    
    for(int i = 1; i <= MAXN; ++i) 
        int v = i;
        if(!visit[v])                                 // 3
            dfs_add(v);                                // 4             
            dfs(depth+1);
            dfs_dec(v);

1）这里的 depth参数用来做计数用，表明本次遍历了多少个结点；
2）当遍历元素达到 MAXN个的时候，输出访问的元素列表；
3）visit[v]用来判断 $v$ 这个元素是否有访问过；
4）dfs_add和 dfs_dec分别表示将结点从访问列表加入和删除；

void dfs_add(int u) 
    visit[u] = true;
    ans[ansSize] = u;
    ++ansSize;


void dfs_dec(int u) 
    --ansSize;
    visit[u] = false;

4）高级应用

a. 枚举

数据范围较小的的排列、组合的穷举。

b. 容斥原理

主要用于组合数学中的计数统计，会在后面的章节详细介绍。

c. 基于状态压缩的动态规划

一般解决棋盘摆放问题， $k$ 进制表示状态，然后利用深搜进行状态转移，会在后面的章节详细介绍。

d.记忆化搜索

某个状态已经被计算出来，就将它 cache 住，利用数组或者哈希表将它的值存储下来，下次要用的时候不需要重新求，此所谓记忆化。本章节会详细讲到记忆化搜索的应用范围。

e.有向图强连通分量

经典的 $T a r j a n$ 算法，求解 $2 - s a t$ 问题的基础，会在后面的章节详细介绍。

f. 无向图割边割点和双连通分量

经典的