夜深人静写算法(三十八)- 整数分块
Posted 英雄哪里出来
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了夜深人静写算法(三十八)- 整数分块相关的知识,希望对你有一定的参考价值。
🙉饭不食,水不饮,题必须刷🙉
还不会C语言,和我一起打卡! 🌞《光天化日学C语言》🌞
LeetCode 太难?上简单题! 🧡《C语言入门100例》🧡
LeetCode 太简单?大神盘他! 🌌《夜深人静写算法》🌌
一、前言
字节大小周取消了!突然感觉很空虚,所以反手就学了个算法。
这个算法的内容比较独立,虽然把它归到数论一栏,但是有一些简单的高中数学基础也能看懂。利用的是整数除法的性质,将一个 O ( n ) O(n) O(n) 的算法优化成 O ( n ) O(\\sqrt n) O(n),听起来是不是挺有意思的,开整!
二、整数分块
1、引例
【例题1】给定 1 ≤ n , k ≤ 1 0 9 1 \\le n,k \\le 10^9 1≤n,k≤109,求 ∑ x = 1 n ⌊ k x ⌋ \\sum_{x=1}^n\\lfloor \\frac k x \\rfloor x=1∑n⌊xk⌋ 其中 ⌊ x ⌋ \\lfloor x \\rfloor ⌊x⌋ 是指实数 x x x 的整数部分。
- 我们可以直接根据题意,写出一个循环语句,代码如下:
#include <iostream>
using namespace std;
int main() {
int n, k;
while(scanf("%d %d", &n, &k) != EOF) {
int ans = 0;
for(int x = 1; x <= n; ++x) {
ans += k / x;
}
printf("%d\\n", ans);
}
return 0;
}
- 容易得知,这样做的时间复杂度是 O ( n ) O(n) O(n) 的。而 n n n 的范围过大,所以需要对这个算法进行优化。
2、引理
- 为了尝试找出优化算法,我们引入如下的一个定理。
【引理1】对于 g ( x ) = ⌊ n x ⌋ g(x) = \\lfloor \\frac n x \\rfloor g(x)=⌊xn⌋ (其中 x x x 为正整数,且 1 ≤ x ≤ n 1 \\le x \\le n 1≤x≤n),则 g ( x ) g(x) g(x) 不同值的个数不会超过 2 n 2\\sqrt n 2n 个。
证明
可以将 g ( x ) g(x) g(x) 的值分成小于 n \\sqrt n n 和 大于等于 n \\sqrt n n 的两部分,如下:
(1)当 g ( x ) < n g(x) \\lt \\sqrt n g(x)<n 时, g ( x ) g(x) g(x) 最多 n − 1 \\sqrt n-1 n−1 个值。
(2)当 g ( x ) ≥ n g(x) \\ge \\sqrt n g(x)≥n 时,则 n ≤ ⌊ n x ⌋ ≤ n x \\sqrt n \\le \\lfloor \\frac n x \\rfloor \\le \\frac n x n≤⌊xn⌋≤xn,从而推导得出 x ≤ n x \\le \\sqrt n x≤n,所以这种情况下 x x x 范围为 [ 1 , n ] [1, \\sqrt n] [1,n],即最多 n \\sqrt n n 个值,自然 g ( x ) g(x) g(x) 也就最多 n \\sqrt n n 个值。
- 综上所述, g ( x ) g(x) g(x) 的值不会超过 2 n 2\\sqrt n 2n 个值。
- 以上就是整数分块的核心。
三、整数分块的性质
1、单调性
- 如图三-1-1所示,代表的是函数 g ′ ( x ) = 25 x g'(x) = \\frac {25} x g′(x)=x25 的图像。这是一个单调不增的函数,即随着 x x x 的增大, g ′ ( x ) g'(x) g′(x) 越来越小。
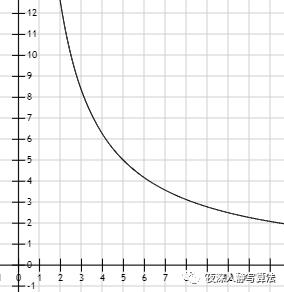
- g ( x ) = ⌊ n x ⌋ g(x) = \\lfloor \\frac n x \\rfloor g(x)=⌊xn⌋ 的单调性和 g ′ ( x ) = n x g'(x) = \\frac n x g′(x)=xn 是一致的,所以 g ( x ) g(x) g(x) 也是单调不增的。
2、连续性
- 结合【引理1】和单调性,要把 n n n 个 x x x 映射到 n \\sqrt n n 个 g ( x ) g(x) g(x),必然有一部分的 g ( x ) g(x) g(x) 值是连续相同的。
- 如图三-2-1所示, n = 25 n=25 n=25 的情况如下:

- 不同颜色代表的不同整数分块,值相同的一定是连续的,所以对于每个 g ( x ) g(x) g(x) 的值(也就是上图中的 ⌊ n x ⌋ \\lfloor \\frac n x \\rfloor ⌊xn⌋ 的值)我们只需要知道一个区间即可。
3、连续区间
- 连续的区间表示成表格的形式,如图三-3-1所示:
| x ∈ [ l , r ] x \\in [l,r] x∈[l,r] | g ( x ) g(x) g(x) |
|---|---|
| [1,1] | 25 |
| [2,2] | 12 |
| [3,3] | 8 |
| [4,4] | 6 |
| [5,5] | 5 |
| [6,6] | 4 |
| [7,8] | 3 |
| [9,12] | 2 |
| [13,25] | 以上是关于夜深人静写算法(三十八)- 整数分块的主要内容,如果未能解决你的问题,请参考以下文章 |
