夜深人静写算法（二十九）- 数位DP

Posted 2021-05-09 英雄哪里出来

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了夜深人静写算法（二十九）- 数位DP相关的知识，希望对你有一定的参考价值。

一、前言

数位 DP 又称数位动态规划，在 LeetCode 上属于难题，而 ACM 竞赛中属于中等题，甚至可以说是模板题。
数位 DP 的状态设计千变万化，但万变不离其宗，只要确定这个题是用数位 DP 求解，基本就很容易把状态套出来。当然，对于刚接触动态规划的同学，建议先看下背包问题、最长单调子序列、最长公共子序列、记忆化搜索等基础内容，对状态机和状态转移有一个初步的认识，那么，在学习数位 DP 时能够起到事半功倍的效果。

二、数位 DP 简介

1、数位 DP 定义

数位 DP 又称数位动态规划，一般可以从题干就能确定这个题是否可以用数位 DP 来求解。因为数位 DP 的题目一般都描述成如下两种问法之一：

【问法1】给定一个闭区间 $[l, r]$ ，求在这个区间中，满足 某些条件 的数的个数。
【问法2】如果一个数字满足 某些条件，则称之为 $X$ 数，给定闭区间 $[l, r]$ ，求这个区间中 $X$ 数的个数。

这里的 某些条件 决定了状态转移的决策，这样说或许比较抽象，那么接下来，我们通过一个简单的例题来了解下数位DP 的一般求解过程。

2、数位 DP 引例

【例题1】如果一个数的所有位数加起来是 $10$ 的倍数, 则称之为 $\\ number$ ，求区间 $\\le l \\le r \\le 10^{18})$ 内 $\\ number$ 的个数；

对于这个问题，朴素算法就是枚举区间里的每个数，并且判断可行性，时间复杂度为 $o ((r - l) c)$ ， $c = 19$ ，肯定是无法接受的。

1）差分转换

对于区间 $[l, r]$ 内求满足数量的数，可以利用差分法分解问题；
假设 $[0, x]$ 内的 $\\ number$ 数量为 $g_x$ ，那么区间 $[l, r]$ 内的数量就是 $g_r - g_{l-1}$ ；分别用同样的方法求出 $g_r$ 和 $g_{l-1}$ ，再相减即可；
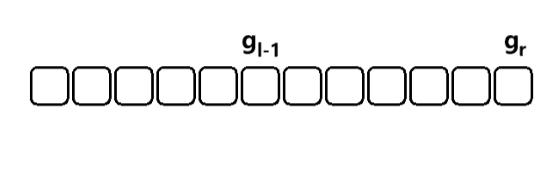
图二-2-1

2）数位性质

如果一个数字 $i$ 满足 $i < x$ ，那么 $i$ 从高到低肯定出现某一位，使得这一位上的数值小于 $x$ 对应位上的数值，并且之前的所有高位都和 $x$ 上的位相等。
举个例子，当 $x = 1314$ 时， $i = 0 a b c$ 、 $i = 12 a b$ 、 $i = 130 a$ 、 $i = 1312$ ，那么对于 $i$ 而言，无论后面的字母取什么数字，都是满足 $i < x$ 这个条件的。
如图二-2-2所示：
图二-2-2
如果我们要求 $g_{1314}$ 的值，可以通过枚举高位：当最高位为0，那么问题就转化成 $g_{999}$ 的子问题；当最高位为1，问题就转化成 $g_{314}$ 的子问题。
$g_{314}$ 可以继续递归求解，而 $g_{999}$ 由于每一位数字范围都是 $[0, 9]$ ，可以转换成一般的动态规划问题来求解。

3）前缀状态

这里的前缀状态就对应了之前提到的 某些条件；
在这个问题中，前缀状态的描述为：一个数字前缀的各位数字之和对10取余（模）的值。
前缀状态的变化过程如图二-2-3所示：
图二-2-3
在【例题1】中，前缀状态的含义是：对于一个数 520 ，我们不需要记录 520 ，而只需要记录 7；对于 52013，我们不需要记录 52013，而只需要记录 1。这样就把原本海量的状态，变成了最多 10 个状态。

3、状态分析

1）状态定义

根据以上的三个信息，我们可以从高位到低位枚举数字 $i$ 的每一位，逐步把问题转化成小问题求解。
我们可以定义 $f (n, s t, l i m)$ 表示剩下还需要考虑 $n$ 位数字，前面已经枚举的高位组成的前缀状态为 $s t$ ，且用 $l i m$ 表示当前第 $n$ 位是否能够取到最大值（对于 $b$ 进制，最大值就是 $b - 1$ ，比如 10 进制状态下，最大值就是 9）时的数字个数。我们来仔细解释一下这三维代表的含义：
1）当前枚举的位是 $n$ 位， $n$ 大的代表高位，小的代表低位；
2） $s t$ 就是前缀状态，在这个问题中，代表了所有已经枚举的高位（即数字前缀）的各位数字之和对10取余（模）。注意：我们并不关心前缀的每一位数字是什么，而只关心它们加和模10之后的值是什么。
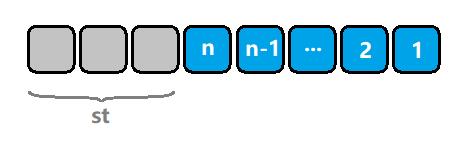
图二-3-1
3） $l i m = t r u e$ 表示的是已经枚举的高位中已经出现了某一位比给定 $x$ 对应位小的数，那么后面枚举的每个数最大值就不再受 $x$ 控制；否则，最大值就应该是 $x$ 的对应位。举例说明，当十进制下的数 $x = 1314$ 时，枚举到高位前三位为 “131”， $l i m = f a l s e$ ，那么第四位数字的区间取值就是 $[0, 4]$ ；而枚举到高位前三位为 “130” 时， $l i m = t r u e$ ，那么第四位数字的区间取值就是 $[0, 9]$ 。参考图二-2-2 加深理解。

2）状态转移

所以，我们根据以上的状态，预处理 $x$ 的每个数位，表示成十进制如下：
$x = d_nd_{n-1}...d_1$
(其中 $d_n$ 代表最高位， $d_1$ 代表最低位)
得出状态转移方程如下：
$\\begin{aligned}& f(n, st, lim) \\\\ &= \\sum_{k=0}^{maxv} f(n-1, (st+k) \\mod 10, lim \\ or \\ (k < maxv))\\end{aligned}$

夜深人静写算法（二十九）- 数位DP

文章目录

一、前言

二、数位 DP 简介

1、数位 DP 定义

2、数位 DP 引例

3、状态分析