交互式多模型算法IMM
Posted 脑壳二
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了交互式多模型算法IMM相关的知识,希望对你有一定的参考价值。
机动目标跟踪——交互式多模型算法IMM
原创不易,路过的各位大佬请点个赞
WX: ZB823618313
机动目标跟踪——交互式多模型算法IMM
1.交互式多模型算法流程
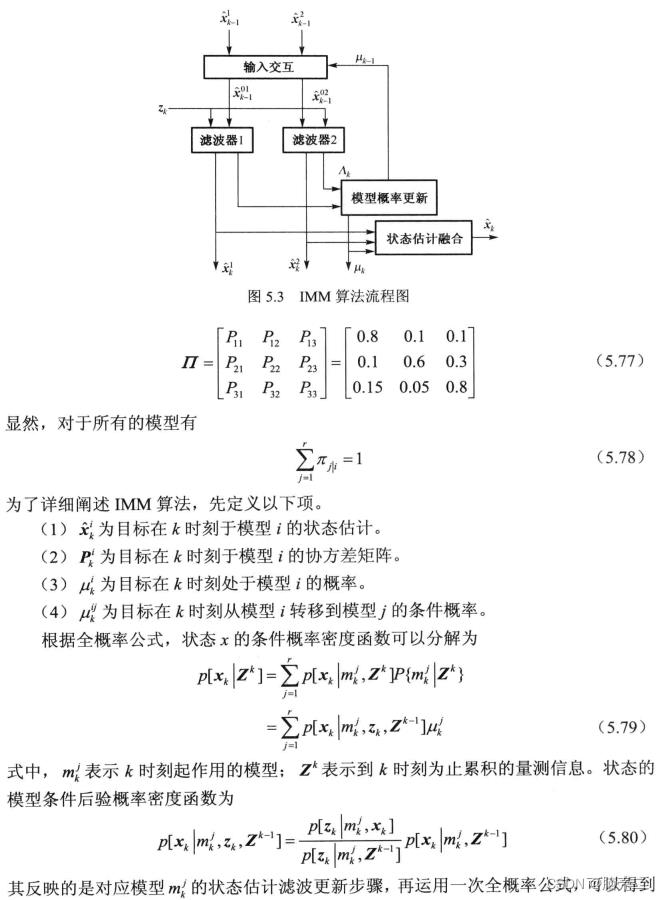
核心思想: IMM算法的基本思想是用多个不同的运动模型匹配机动目标的不同运动模式,不同模型间的转移概率是–个马尔可夫矩阵,目标的状态估计和模型概率的更新使用卡尔曼滤波。其算法流程图如图5.3所示。

2. 交互式多模型:具体推导




3. IMM+KF目标跟踪
WX: ZB823618313
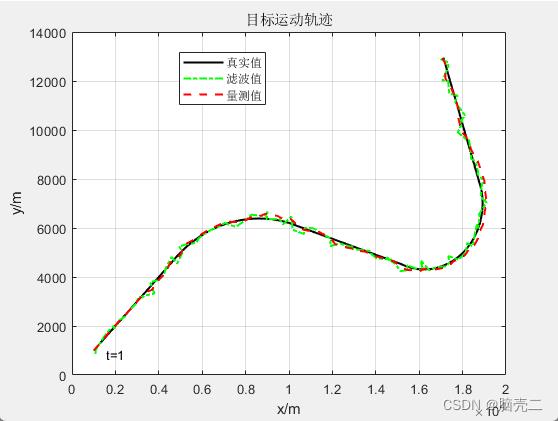
4. IMM+UKF目标跟踪
4.1. 仿真参数
一、目标模型:CV CT CT
第一阶段:1:39s,匀速运动CV
第二阶段:40:71s,匀速圆周运动CT,角速度:
2
∗
π
/
180
;
2*\\pi/180;
2∗π/180;
第三阶段:72:99s,匀速运动CV
第四阶段:100:131s,匀速圆周运动CT,角速度:
−
3
∗
π
/
180
;
-3*\\pi/180;
−3∗π/180;
第五阶段:72:99s,匀速运动CV
CV CT 模型的具体方程形式见另一个博客
二、测量模型:2D主动雷达
在二维情况下,雷达量测为距离和角度
r
k
m
=
r
k
+
r
~
k
b
k
m
=
b
k
+
b
~
k
r_k^m=r_k+\\tilder_k\\\\ b^m_k=b_k+\\tildeb_k
rkm=rk+r~kbkm=bk+b~k
其中
r
k
=
(
x
k
−
x
0
)
+
(
y
k
−
y
0
)
2
)
b
k
=
tan
−
1
y
k
−
y
0
x
k
−
x
0
r_k=\\sqrt(x_k-x_0)^+(y_k-y_0)^2)\\\\ b_k=\\tan^-1\\fracy_k-y_0x_k-x_0\\\\
rk=(xk−x0)+(yk−y0)2)bk=tan−1xk−x0yk−y0
[
x
0
,
y
0
]
[x_0,y_0]
[x0,y0]为雷达坐标,一般情况为0。雷达量测为
z
k
=
[
r
k
,
b
k
]
′
z_k=[r_k,b_k]'
zk=[rk,bk]′。雷达量测方差为
R
k
=
cov
(
v
k
)
=
[
σ
r
2
0
0
σ
b
2
]
R_k=\\textcov(v_k)=\\beginbmatrix\\sigma_r^2 & 0 \\\\0 & \\sigma_b^2 \\endbmatrix
Rk=cov(vk)=[σr200σb2]且
σ
r
=
120
m
\\sigma_r=120m
σr=120m,
σ
b
=
80
m
r
a
d
\\sigma_b=80mrad
σb=80mrad。
三、性能评估
RMSE(Root mean-squared error):蒙塔卡罗次数
M
=
500
M=500
M=500,
x
^
k
∣
k
i
\\hatx_k|k^i
x^k∣ki为第
i
i
i次仿真得到的估计。
RMSE
(
x
^
)
=
1
M
∑
i
=
1
M
(
x
k
−
x
^
k
∣
k
i
)
(
x
k
−
x
^
k
∣
k
i
)
′
\\textRMSE(\\hatx)=\\sqrt\\frac1M\\sum_i=1^M(\\mathbfx_k-\\hat\\mathbfx_k|k^i)(\\mathbfx_k-\\hat\\mathbfx_k|k^i)'
RMSE(x^)=M1i=1∑M(xk−x^k∣ki)(xk−x^k∣ki)′
Position RMSE
(
x
^
)
=
1
M
∑
i
=
1
M
(
x
k
−
x
^
k
∣
k
i
)
2
+
(
y
k
−
y
^
k
∣
k
i
)
2
\\textPosition RMSE(\\hatx)=\\sqrt\\frac1M\\sum_i=1^M(x_k-\\hatx_k|k^i)^2+(y_k-\\haty_k|k^i)^2
Position RMSE(x^)=M1i=1∑M(xk−x^k∣ki)2+(yk−y^k∣ki以上是关于交互式多模型算法IMM的主要内容,如果未能解决你的问题,请参考以下文章
交互式多模型IMM算法实现难点——模型维数不同(基于CVCTCA模型的IMM算法)