机动目标运动分析——IMM篇

Posted 2022-12-10 Nickyfks

目录

1.交互式多模型算法

1.1 交互式多模型算法介绍

1.2 交互式多模型算法流程

1.3 交互式多模型算法仿真分析

2.参考文献

---

1.交互式多模型算法

1.1 交互式多模型算法介绍

交互式多模型算法（Interacting Multiple Model, IMM）是由Blom和Bar-shalom提出的一种具有马尔可夫切换系数的算法，该算法有多种模型并行工作，目标状态估计是多个滤波器交互作用的结果。

1.2 交互式多模型算法流程

IMM算法在机动目标跟踪领域已经应用的非常广泛，此处不再赘述其推导过程，引用一篇优秀文章总结的大致步骤如下：

上述给出的大致步骤仅给出了IMM算法的大致框架，IMM常与贝叶斯类估计算法结合，如EKF、UKF、PF等，结合后的算法常称为IMM-EKF、IMM-UKF、IMM-PF等。贝叶斯类估计算法的公式具体可参考我的其他博客。

EKF算法

目标跟踪常用算法——EKF篇_Nickyfks的博客-CSDN博客

UKF算法

目标跟踪常用算法——UKF篇_Nickyfks的博客-CSDN博客

EPF、UPF算法

目标跟踪常用算法——EPF、UPF篇_Nickyfks的博客-CSDN博客

1.3 交互式多模型算法仿真分析

假设一目标在二维平面内做匀速直线运动与匀速转弯运动的组合机动，观测站处于原点且保持静止，无站址误差。观测站可以实时测量到目标与观测站之间的距离以及方位角(北偏东)。适用IMM-EKF与IMM-UKF算法对机动目标进行跟踪。蒙特卡洛仿真50次，并将RMSE与CRLB进行对比。

	目标初始状态			量测误差		过程噪声
二维	(1000m,2500m,-10m/s,-15m/s)			100m，1°		1e-4m/s2
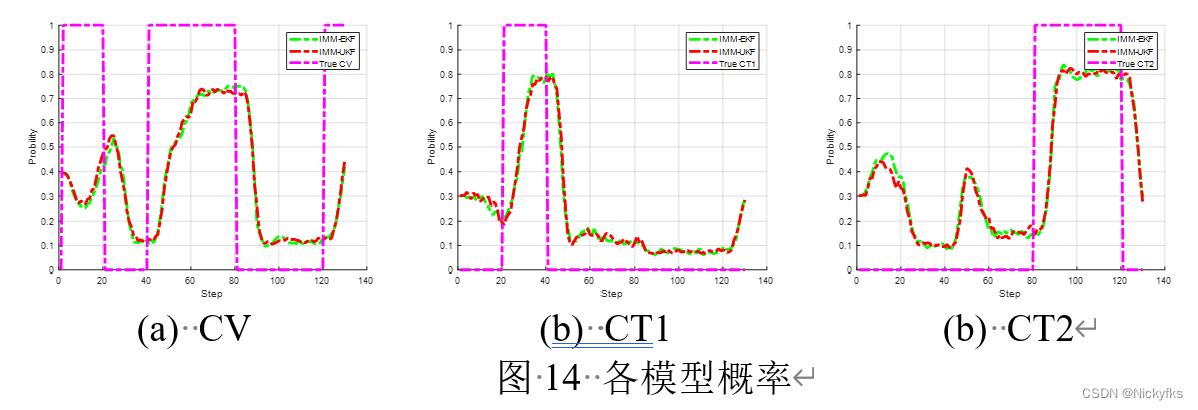
1-20		21-40	41-80		81-120		121-130
CV		CT1(w=1.3°/s)	CV		CT2(w=-0.8°/s)		CV

 下面给出IMM-EKF算法的部分代码

%% IMM-EKF
clc;clear all;
% close all;

%% Initialization
MC=50; % Monte-Carlo Times
N=130; % Sampling Times
T=2; % Sampling Interval
syms omega
F_CV=[1 0 T 0;0 1 0 T;0 0 1 0;0 0 0 1]; % State transition matrix（CV）
F_CT=[1 0 sin(omega*T)/omega (cos(omega*T)-1)/omega;0 1 (1-cos(omega*T))/omega sin(omega*T)/omega;0 0 cos(omega*T) -sin(omega*T);0 0 sin(omega*T) cos(omega*T)];% State Transiton Matrix（CT）
G=[T^2/2 0;0 T^2/2;T 0;0 T]; % Disturbance matrix
w=[1e-4;1e-4]; % System noise matrix
Q=[w(1)^2,0;0,w(2)^2];
r_ranging=1; % Measurement noise (m)
r_bearing=0.5*pi/180; % Measurement noise (rad)
R=[r_ranging^2,0;0,r_bearing^2];
Target_num=1;
X(:,1)=[1000,3500,-10,-15]';
Station_num=1;
Station=zeros(4,N);
Model_num=3;
Time1=20; % 0-Time1 CV
omega1=1.3*pi/180;
F_CT1=[1 0 sin(omega1*T)/omega1 (cos(omega1*T)-1)/omega1;0 1 (1-cos(omega1*T))/omega1 sin(omega1*T)/omega1;0 0 cos(omega1*T) -sin(omega1*T);0 0 sin(omega1*T) cos(omega1*T)];% State Transiton Matrix（CT）
Time2=40; % Time1-Time2 CT
Time3=80; % Time2-Time3 CV
omega2=-0.8*pi/180;
F_CT2=[1 0 sin(omega2*T)/omega2 (cos(omega2*T)-1)/omega2;0 1 (1-cos(omega2*T))/omega2 sin(omega2*T)/omega2;0 0 cos(omega2*T) -sin(omega2*T);0 0 sin(omega2*T) cos(omega2*T)];% State Transiton Matrix（CT）
Time4=120; % Time3-Time4 CT
Time5=N; % Time4-Time5 CV
F_all=[F_CV,F_CT1,F_CT2];

%% Target State
[X,mu_true]=Target_State(X,F_all,G,w,Time1,Time2,Time3,Time4,Time5);

2.参考文献

石章松. 目标定位跟踪方法与实践[M].  电子工业出版社,2019.

廖永汉, 朱胜利, 彭冬亮.基于IMM滤波器的纯方位机动目标跟踪[J].火力与指挥控制,2010, 35 (01): 20-23.