认识堆和堆排序

Posted 2022-11-28 dxj1016

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了认识堆和堆排序相关的知识，希望对你有一定的参考价值。

10、堆

10.1、完全二叉树

10.2、大跟堆

在一个完全二叉树里，每一颗子树的最大值就是头结点的值，满足这个条件就是大跟堆。

10.3、小跟堆

在一个完全二叉树中，每一颗子树的最小值就是他的头结点，满足这个条件就是小跟堆。

怎么让一个完全二叉树变成大跟堆呢？

一开始heapsize是为0的，然后5进来的时候，就放到heapsize为0的位置，然后heapsize变为1了，再进来一个数3的时候，将其放到heapsize为1的位置，然后heapsieze变为2；在进来6的时候，将其放到heapsize为2的位置，heapsize变为3；这时候根据父结点的寻找公式来确定子节点的父结点是啥，所以6可以确定他的父结点是5，这时候就要比较父结点跟子节点，子节点要是比父结点大，就得交换两者位置，如果小的话就不用交换位置，继续处理进来的另一个数。通过父结点的比较可以每次进来一个数都能将其调整为大跟堆的形式。

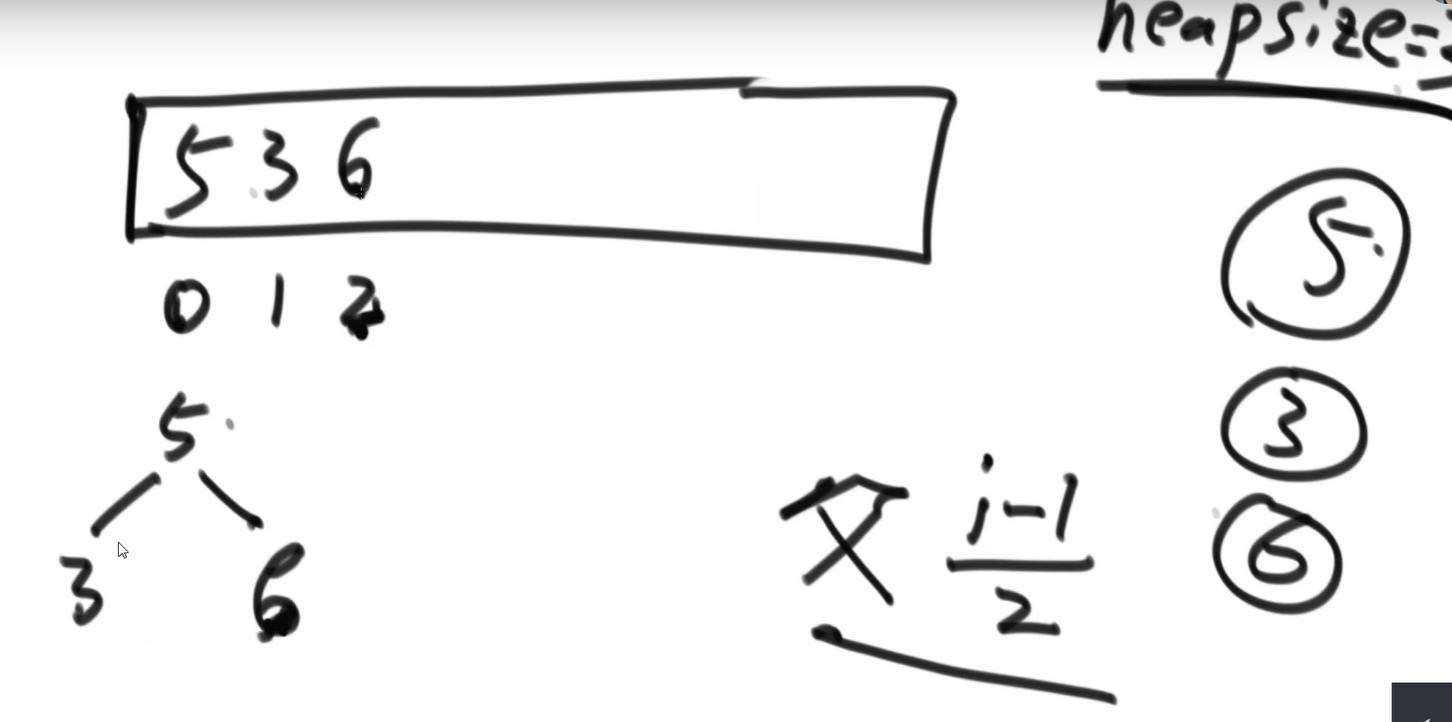
要将大跟堆中的最大值拿掉，怎么让原本的大跟堆还保持大跟堆的状态。

大跟堆的头结点跟最后一个结点的值交换，然后heapsize减小1；heapsize减一之后就以为这之前的头结点也就是换到最后一个结点的值是不存在大跟堆了，因为heapsize减一后如果还要最后一个结点就是下标越界了。

调换之后可能之前的大跟堆已经不再是大跟堆的结构了，所以需要再次调整为大跟堆，怎么调整呢？

从头结点开始，找他的子节点中的最大值，然后最大值跟父结点交换。

问题：如果现在要修改大跟堆中的i位置的某个值为其他的值，那么怎么保证这个完全二叉树还是大跟堆呢？

首先看他修改后的值跟之前的值比较，如果比之前的大，那么就跟上面的进行一个比较，也就是headfy操作。如果比之前的小，就跟下面的进行比较。

堆其实就是只有两个操作，一个是heapsize操作一个是headfy操作。

package 左神算法.堆;

public class Heap 
    public static void main(String[] args) 
        int[] arr = 7, 3, 6, 5, 8;
        int index = 4;
        int heapSize = 0;
        heapInsert(arr, index);
        heapify(arr, index, heapSize);
        for (int i = 0; i < arr.length; i++) 
            System.out.print(arr[i] + " ");
        
    
//某个数现在处在index位置，往上继续移动
    public static void heapInsert(int[] arr, int index) 
        while (arr[index] > arr[(index - 1) / 2]) 
            swap(arr, index, (index - 1) / 2);
            index = (index - 1) / 2;
        
    

    //某个数在index位置，能否往下移动
    public static void heapify(int[] arr, int index, int heapSize) 
        int left = index * 2 + 1;//左孩子的下标
        while (left < heapSize) //下方还有孩子的时候
//            两个孩子中，谁的值大，把下标给largest
            int largest = left + 1 < heapSize && arr[left + 1] > arr[left] ? left + 1 : left;
//            父和孩子之间，谁的值大，把下标给largest
            largest = arr[largest] > arr[index] ? largest : index;
            if (largest == index) 
                break;
            
            swap(arr, largest, index);
            index = largest;
            left = index * 2 + 1;
        
    
    public static void swap(int[] arr, int i, int j) 
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    

/*
8 7 6 5 3 
 */