堆和堆排序

Posted 2021-05-01 数学算法实验室

今天讲的堆相关知识很重要哦

堆

堆的定义： 堆可以定义成一棵二叉树，树上的每个节点都必须包含一个键，并且须满足以下两个条件： ①这棵树只有最后一层最右边的元素有可能缺位； ②每个节点的键都必须大于其子女的键（简称父母优势要求）。

大家可根据上面所给出的堆的定义来判断以下三棵树中哪棵树是堆。

在堆中，键值是从上到下排序的，不存在从左到右的关系，也就是说同一层的节点没有任何关系。 我们在上面的定义中使用了二叉树来理解堆，这样的做法的确有助于我们认识和理解堆，但在实际实现的过程中，用数组会简单高效得多。 那么堆用数组该如何表示呢？ 方法是在数组1到n的位置用从上到下、从左到右的顺序记录堆的元素。 其中数组0处设为空，或者放置一个限位器（即它的值大于堆中任何一个元素）。

堆的重要特性：

①  只存在一棵n个节点的完全二叉树，它的高度为.

②  堆的最大元素在根处。

③  堆的任一节点以及该节点的子孙也是一个堆。

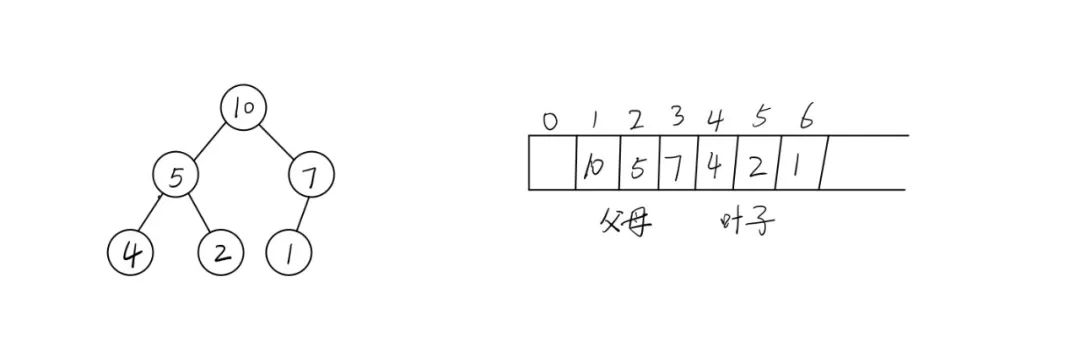
④  堆可以用数组表示，方法前文已经给出。 在这种方法中，父母节点的键总是位于前个位置中； 而在数组中，对于一个位于父母位置i（1<=i<=n/2）的键来说，它的子女将会位于2i和2i+1.

因此，我们也可以把堆定义成一个数组，这个数组满足以下条件： 对于i=1,，，n/2, H[i] >=max(H[2i],H[2i+1])

构造堆

针对键给定的列表，我们如何构造一个堆呢？ 我们主要有两种做法： 第一种是自底向上堆构造法。 在初始化一棵含n个节点的完全二叉树时，我们按照给定的顺序来放置键。 以下为对这棵树的“堆化”步骤： 从最后一层父母节点到根，检查它们是否满足父母优势要求→若不满足，把节点的键K和它子女的最大键交换→K的父母优势要求满足。 （这个算法并不是从下到上一次就能成功的，在子节点的母节点满足优势之后，子节点可能出现不满足优势的情况）

def HeapBottomUp(H): n=len(H)-1 for i in range(n//2,0,-1): k,v=i,H[i] heap=False while not heap and 2*k<=n: j=2*k if j<n and H[j]<H[j+1]:j=j+1 if v>=H[j]:heap = True else:H[k],k=H[j],j H[k]=v return HH=[0,8,4,5,6,7,3,1]print(HeapBottomUp(H))

这个算法在最坏情况下的效率是o(n)级别的，并且具体来说在一个规模为n的堆只需要不到2n次比较就能完成。

  另一种算法是通过把一个新的键K插入到预先构造好的堆中，来构造一个新堆。 一般情况下我们称这种算法为自顶而下堆构造算法。 那么如何将一个新的键插入到堆中呢？ 下面请看详细步骤： 首先我们将K插入到当前堆的最后一个叶子后面，然后拿K和它父母的键进行比较，如果后者大于K则停止比较，否则交换父母节点与该节点的键值并把K和它新的父母进行比较，直到找到一个和合适的位置。

显然，插入操作的次数不会超过堆的高度——log n，所以插入的时间效率属于o(log n)，

那么我们知道了如何进行插入操作，那么我们也想知道该如何进行删除呢？ 这里说一个简单一点的情况，删除堆的最大值（看完这个的读者估计自己也可以想出删除任意键的算法了）

第一步： 根的键和堆的最后一个元素进行交换

第二步： 堆的规模减一

第三步： 按照自底而上堆构造的算法对这棵树进行堆化

堆排序

既然现在大家知道什么是堆了，那么我们便开始介绍一下今天的主角——堆排序

堆排序的算法 简单来说就是下面的两个操作：

1、构造堆： 将一个给定数组构造一个堆

2、删除最大键： 对剩下的堆进行n-1次删除最大值的操作

  下面用一幅图来看一下堆排序的具体操作吧

def HeapSort(H): n=len(H)-1 Sorted=[] while n>1: H=HeapBottomUp(H) Sorted.append(H[1]) del(H[1]) n=len(H)-1 Sorted.append(H[1]) return Sorted
print(HeapSort(H))

堆排序的效率分析： 我们已经知道了构造一个堆的时间效率是o（n），所以我们只需要研究第二阶段的时间效率就ok了。 在把n的规模减到2的过程，为了消去根的键，需要进行小于n*logn次运算，所以对于两个阶段的总效率仍旧是属于n*logn的。 因此，堆排序在效率上和归并排序有的一拼，但在随机文件的计时实验中发现，堆排序并没有表现出快速排序一样优秀的性能。

以上就是今天的全部内容了，如果你喜欢的话，点个在看吧，你的支持是我最大的动力

参考书籍   《算法设计与分析基础》

审稿：傻傻小姐

代码：呆呆

侵删