微软面试题解析：丑数系列算法

Posted 2022-08-22 程序员小灰

读完本文，可以去力扣解决如下题目：

263. 丑数（简单）

264. 丑数 II（中等）

1201. 丑数 III（中等）

313. 超级丑数（中等）

最近读者群里有个读者跟我私信，说去面试微软遇到了一系列和数学相关的算法题，直接懵圈了。我看了下题目，发现这些题其实就是 LeetCode 上面「丑数」系列问题的修改版。

首先，「丑数」系列问题属于会者不难难者不会的类型，因为会用到些数学定理嘛，如果没有专门学过，靠自己恐怕是想不出来的。

另外，这类问题而且非常考察抽象联想能力，因为它除了数学定理之外，还需要你把题目抽象成链表相关的题目运用双指针技巧，或者抽象成数组相关的题目运用二分搜索技巧。

那么今天我就来用一篇文章把所有丑数相关的问题一网打尽，看看这类问题能够如何变化，应该如何解决。

丑数 I

首先是力扣第 263 题「丑数」，题目给你输入一个数字n，请你判断n是否为「丑数」。所谓「丑数」，就是只包含质因数2、3和5的正整数。

函数签名如下：

boolean isUgly(int n)

比如 12 = 2 x 2 x 3 就是一个丑数，而 42 = 2 x 3 x 7 就不是一个丑数。

这道题其实非常简单，前提是你知道算术基本定理（正整数唯一分解定理）：

任意一个大于 1 的自然数，要么它本身就是质数，要么它可以分解为若干质数的乘积。

既然任意一个大于一的正整数都可以分解成若干质数的乘积，那么丑数也可以被分解成若干质数的乘积，且这些质数只能是 2, 3 或 5。

有了这个思路，就可以实现isUgly函数了：

public boolean isUgly(int n) 
    if (n <= 0) return false;
    // 如果 n 是丑数，分解因子应该只有 2, 3, 5
    while (n % 2 == 0) n /= 2;
    while (n % 3 == 0) n /= 3;
    while (n % 5 == 0) n /= 5;
    // 如果能够成功分解，说明是丑数
    return n == 1;

丑数 II

接下来提升难度，看下力扣第 264 题「丑数 II」，现在题目不是让你判断一个数是不是丑数，而是给你输入一个n，让你计算第n个丑数是多少，函数签名如下：

int nthUglyNumber(int n)

比如输入n = 10，函数应该返回 12，因为从小到大的丑数序列为1, 2, 3, 4, 5, 6, 8, 9, 10, 12，第 10 个丑数是 12（注意我们把 1 也算作一个丑数）。

这道题很精妙，你看着它好像是道数学题，实际上它却是一个合并多个有序链表的问题，同时用到了筛选素数的思路。

首先，我在前文中也讲过高效筛选质数的「筛数法」：一个质数和除 1 以外的其他数字的乘积一定不是质数，把这些数字筛掉，剩下的就是质数。

Wikipedia 的这幅图很形象：

基于筛数法的思路和丑数的定义，我们不难想到这样一个规律：如果一个数x是丑数，那么x * 2, x * 3, x * 5都一定是丑数。

如果我们把所有丑数想象成一个从小到大排序的链表，就是这个样子：

1 -> 2 -> 3 -> 4 -> 5 -> 6 -> 8 -> ...

然后，我们可以把丑数分为三类：2 的倍数、3 的倍数、5 的倍数。这三类丑数就好像三条有序链表，如下：

能被 2 整除的丑数：

1*2 -> 2*2 -> 3*2 -> 4*2 -> 5*2 -> 6*2 -> 8*2 ->...

能被 3 整除的丑数：

1*3 -> 2*3 -> 3*3 -> 4*3 -> 5*3 -> 6*3 -> 8*3 ->...

能被 5 整除的丑数：

1*5 -> 2*5 -> 3*5 -> 4*5 -> 5*5 -> 6*5 -> 8*5 ->...

我们如果把这三条「有序链表」合并在一起并去重，得到的就是丑数的序列，其中第n个元素就是题目想要的答案：

1 -> 1*2 -> 1*3 -> 2*2 -> 1*5 -> 3*2 -> 4*2 ->...

所以这里就和“合并两条有序链表”的思路基本一样了，先看下合并有序链表的核心解法代码：

ListNode mergeTwoLists(ListNode l1, ListNode l2) 
    // 虚拟头结点存储结果链表，p 指针指向结果链表
    ListNode dummy = new ListNode(-1), p = dummy;
    // p1, p2 分别在两条有序链表上
    ListNode p1 = l1, p2 = l2;
    
    while (p1 != null && p2 != null) 
        // 比较 p1 和 p2 两个指针
        // 将值较小的的节点接到结果链表
        if (p1.val > p2.val) 
            p.next = p2;
            p2 = p2.next;
         else 
            p.next = p1;
            p1 = p1.next;
        
        // p 指针不断前进
        p = p.next;
    
    // 省略部分非核心代码...

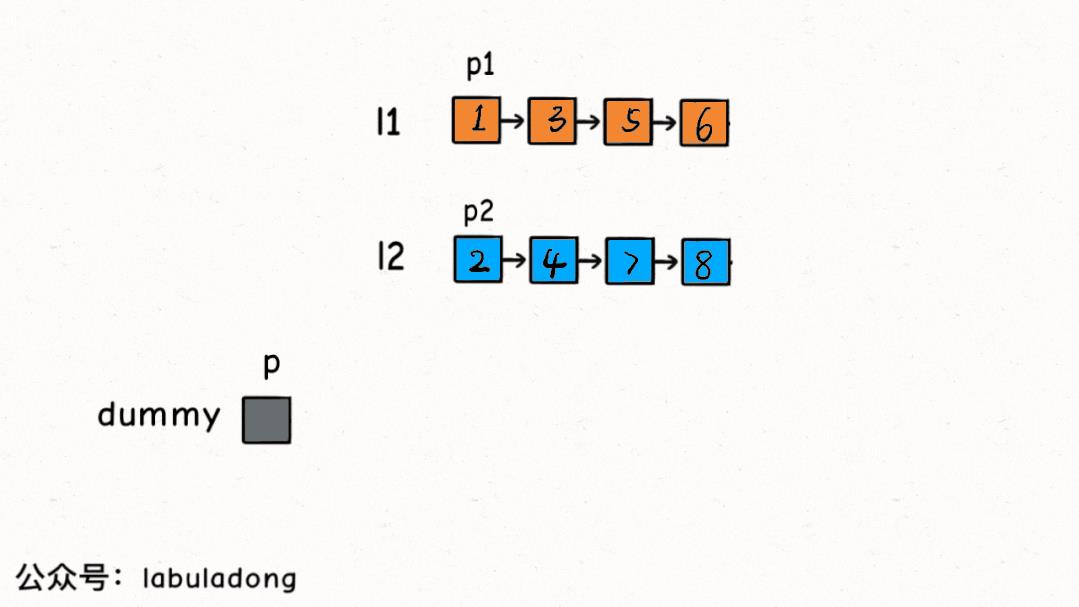
对于这道题，我们抽象出三条有序的丑数链表，合并这三条有序链表得到的结果就是丑数序列，其中第n个丑数就是题目想要的答案。

类比合并两个有序链表，看下这道题的解法代码：

int nthUglyNumber(int n) 
    // 可以理解为三个指向有序链表头结点的指针
    int p2 = 1, p3 = 1, p5 = 1;
    // 可以理解为三个有序链表的头节点的值
    int product2 = 1, product3 = 1, product5 = 1;
    // 可以理解为最终合并的有序链表（结果链表）
    int[] ugly = new int[n + 1];
    // 可以理解为结果链表上的指针
    int p = 1;

    // 开始合并三个有序链表，找到第 n 个丑数时结束
    while (p <= n) 
        // 取三个链表的最小结点
        int min = Math.min(Math.min(product2, product3), product5);
        // 将最小节点接到结果链表上
        ugly[p] = min;
        p++;
        // 前进对应有序链表上的指针
        if (min == product2) 
            product2 = 2 * ugly[p2];
            p2++;
        
        if (min == product3) 
            product3 = 3 * ugly[p3];
            p3++;
        
        if (min == product5) 
            product5 = 5 * ugly[p5];
            p5++;
        
    
    // 返回第 n 个丑数
    return ugly[n];

我们用p2, p3, p5分别代表三条丑数链表上的指针，用product2, product3, product5代表丑数链表上节点的值，用ugly数组记录有序链表合并之后的结果。

有了之前的铺垫和类比，你应该很容易看懂这道题的思路了，接下来我们再提高一点难度。

超级丑数

看下力扣第 313 题「超级丑数」，这道题给你输入一个质数列表primes和一个正整数n，请你计算第n个「超级丑数」。所谓超级丑数是一个所有质因数都出现在primes中的正整数，函数签名如下：

int nthSuperUglyNumber(int n, int[] primes)

如果让primes = [2, 3, 5]就是上道题，所以这道题是上道题的进阶版。

不过思路还是类似的，你还是把每个质因子看做一条有序链表，上道题相当于让你合并三条有序链表，而这道题相当于让你合并len(primes)条有序链表，也就是「合并 K 条有序链表」的思路。

注意我们在上道题抽象出了三条链表，需要p2, p3, p5作为三条有序链表上的指针，同时需要product2, product3, product5记录指针所指节点的值，每次循环用min函数计算最小头结点。

这道题相当于输入了len(primes)条有序链表，我们不能用min函数计算最小头结点了，而是要用优先级队列来计算最小头结点，同时依然要维护链表指针、指针所指节点的值，我们可以用一个三元组来保存这些信息。

你结合“合并 K 条有序链表”的思路就能理解这道题的解法：

int nthSuperUglyNumber(int n, int[] primes) 
    // 优先队列中装三元组 int[] product, prime, pi
    // 其中 product 代表链表节点的值，prime 是计算下一个节点所需的质数因子，pi 代表链表上的指针
    PriorityQueue<int[]> pq = new PriorityQueue<>((a, b) -> 
        // 优先级队列按照节点的值排序
        return a[0] - b[0];
    );

    // 把多条链表的头结点加入优先级队列
    for (int i = 0; i < primes.length; i++) 
        pq.offer(new int[] 1, primes[i], 1 );
    

    // 可以理解为最终合并的有序链表（结果链表）
    int[] ugly = new int[n + 1];
    // 可以理解为结果链表上的指针
    int p = 1;

    while (p <= n) 
        // 取三个链表的最小结点
        int[] pair = pq.poll();
        int product = pair[0];
        int prime = pair[1];
        int index = pair[2];

        // 避免结果链表出现重复元素
        if (product != ugly[p - 1]) 
            // 接到结果链表上
            ugly[p] = product;
            p++;
        

        // 生成下一个节点加入优先级队列
        int[] nextPair = new int[]ugly[index] * prime, prime, index + 1;
        pq.offer(nextPair);
    
    return ugly[n];

接下来看下第四道丑数题目，也是今天的压轴题。

丑数 III

这是力扣第 1201 题「丑数 III」，看下题目：

给你四个整数：n, a, b, c，请你设计一个算法来找出第n个丑数。其中丑数是可以被a或b或c整除的正整数。

这道题和之前题目的不同之处在于它改变了「丑数」的定义，只要一个正整数x存在a, b, c中的任何一个因子，那么x就是丑数。

比如输入n = 7, a = 3, b = 4, c = 5，那么算法输出 10，因为符合条件的丑数序列为3, 4, 5, 6, 8, 9, 10, ...，其中第 7 个数字是 10。

有了之前几道题的铺垫，你肯定可以想到把a, b, c的倍数抽象成三条有序链表：

1*3 -> 2*3 -> 3*3 -> 4*3 -> 5*3 -> 6*3 -> 7*3 ->...
1*4 -> 2*4 -> 3*4 -> 4*4 -> 5*4 -> 6*4 -> 7*4 ->...
1*5 -> 2*5 -> 3*5 -> 4*5 -> 5*5 -> 6*5 -> 7*5 ->...

然后将这三条链表合并成一条有序链表并去除重复元素，这样合并后的链表元素就是丑数序列，我们从中找到第n个元素即可：

1*3 -> 1*4 -> 1*5 -> 2*3 -> 2*4 -> 3*3 -> 2*5 ->...

有了这个思路，可以直接写出代码：

public int nthUglyNumber(int n, int a, int b, int c) 
    // 可以理解为三个有序链表的头结点的值
    // 由于数据规模较大，用 long 类型
    long productA = a, productB = b, productC = c;
    // 可以理解为合并之后的有序链表上的指针
    int p = 1;

    long min = -666;

    // 开始合并三个有序链表，获取第 n 个节点的值
    while (p <= n) 
        // 取三个链表的最小结点
        min = Math.min(Math.min(productA, productB), productC);
        p++;
        // 前进最小结点对应链表的指针
        if (min == productA) 
            productA += a;
        
        if (min == productB) 
            productB += b;
        
        if (min == productC) 
            productC += c;
        
    
    return (int) min;

这个思路应该是非常简单的，但是提交之后并不能通过所有测试用例，会超时。

注意题目给的数据范围非常大，a, b, c, n的大小可以达到 10^9，所以即便上述算法的时间复杂度是O(n)，也是相对比较耗时的，应该有更好的思路能够进一步降低时间复杂度。

这道题的正确解法难度比较大，难点在于你要把一些数学知识和 二分搜索技巧 结合起来才能高效解决这个问题。

首先，我们可以定义一个单调递增的函数f：

f(num, a, b, c)计算[1..num]中，能够整除a或b或c的数字的个数，显然函数f的返回值是随着num的增加而增加的（单调递增）。

题目让我们求第n个能够整除a或b或c的数字是什么，也就是说我们要找到一个最小的num，使得f(num, a, b, c) == n。

这个num就是第n个能够整除a或b或c的数字。

根据 二分查找的实‍际运用 给出的思路模板，我们得到一个单调函数f，想求参数num的最小值，就可以运用搜索左侧边界的二分查找算法了：

int nthUglyNumber(int n, int a, int b, int c) 
    // 题目说本题结果在 [1, 2 * 10^9] 范围内，
    // 所以就按照这个范围初始化两端都闭的搜索区间
    int left = 1, right = (int) 2e9;
    // 搜索左侧边界的二分搜索
    while (left <= right) 
        int mid = left + (right - left) / 2;
        if (f(mid, a, b, c) < n) 
            // [1..mid] 中符合条件的元素个数不足 n，所以目标在右半边
            left = mid + 1;
         else 
            // [1..mid] 中符合条件的元素个数大于 n，所以目标在左半边
            right = mid - 1;
        
    
    return left;


// 函数 f 是一个单调函数
// 计算 [1..num] 之间有多少个能够被 a 或 b 或 c 整除的数字
long f(int num, int a, int b, int c) 
    // 下文实现

搜索左侧边界的二分搜索代码模板在 二分查找框架详解 中讲过，没啥可说的，关键说一下函数f怎么实现，这里面涉及容斥原理以及最小公因数、最小公倍数的计算方法。

首先，我把[1..num]中能够整除a的数字归为集合A，能够整除b的数字归为集合B，能够整除c的数字归为集合C，那么len(A) = num / a, len(B) = num / b, len(C) = num / c，这个很好理解。

但是f(num, a, b, c)的值肯定不是num / a + num / b + num / c这么简单，因为你注意有些数字可能可以被a, b, c中的两个数或三个数同时整除，如下图：

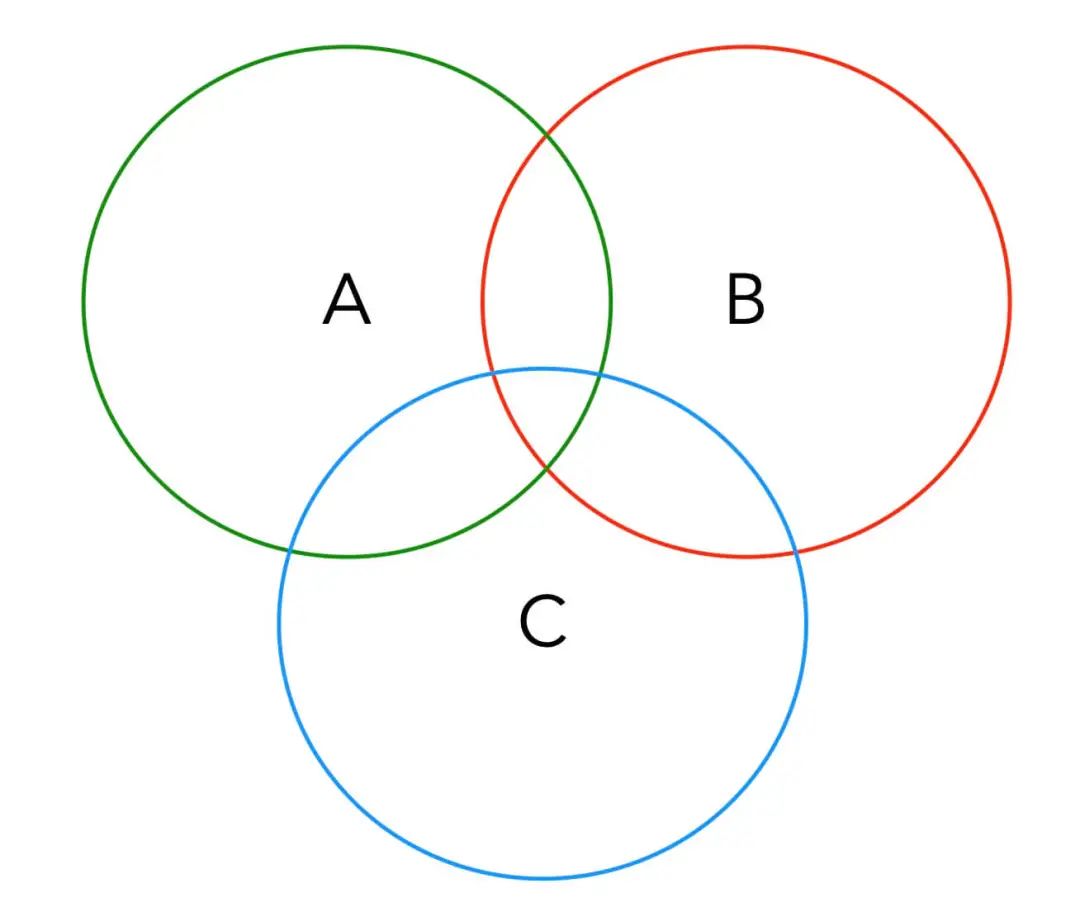
按照容斥原理，这个集合中的元素应该是：A + B + C - A ∩ B - A ∩ C - B ∩ C + A ∩ B ∩ C。结合上图应该很好理解。

问题来了，A, B, C三个集合的元素个数我们已经算出来了，但如何计算像A ∩ B这种交集的元素个数呢？

其实也很容易想明白，A ∩ B的元素个数就是num / lcm(a, b)，其中lcm是计算最小公倍数（Least Common Multiple）的函数。

类似的，A ∩ B ∩ C的元素个数就是num / lcm(lcm(a, b), c)的值。

现在的问题是，最小公倍数怎么求？

直接记住定理吧：lcm(a, b) = a * b / gcd(a, b)，其中gcd是计算最大公因数（Greatest Common Divisor）的函数。

现在的问题是，最大公因数怎么求？这应该是经典算法了，我们一般叫辗转相除算法（或者欧几里得算法）。

好了，套娃终于套完了，我们可以把上述思路翻译成代码就可以实现f函数，注意本题数据规模比较大，有时候需要用long类型防止int溢出：

// 计算最大公因数（辗转相除/欧几里得算法）
long gcd(long a, long b) 
    if (a < b) 
        // 保证 a > b
        return gcd(b, a);
    
    if (b == 0) 
        return a;
    
    return gcd(b, a % b);


// 最小公倍数
long lcm(long a, long b) 
    // 最小公倍数就是乘积除以最大公因数
    return a * b / gcd(a, b);


// 计算 [1..num] 之间有多少个能够被 a 或 b 或 c 整除的数字
long f(int num, int a, int b, int c) 
    long setA = num / a, setB = num / b, setC = num / c;
    long setAB = num / lcm(a, b);
    long setAC = num / lcm(a, c);
    long setBC = num / lcm(b, c);
    long setABC = num / lcm(lcm(a, b), c);
    // 集合论定理：A + B + C - A ∩ B - A ∩ C - B ∩ C + A ∩ B ∩ C
    return setA + setB + setC - setAB - setAC - setBC + setABC;

实现了f函数，结合之前的二分搜索模板，时间复杂度下降到对数级别，即可高效解决这道题目了。

以上就是所有「丑数」相关的题目，用到的知识点有算术基本定理、容斥原理、辗转相除法、链表双指针合并有序链表、二分搜索模板等等。

如果没做过类似的题目可能很难想出来，但只要做过，也就手到擒来了。所以我说这种数学问题属于会者不难，难者不会的类型。