算法leetcode每日一练二叉搜索树的范围和

Posted 2022-05-18 二当家的白帽子

---

文章目录

• 二叉搜索树的范围和：
• 样例 1：
• 样例 2：
• 提示：
• 分析
• 题解
• • java
  • c
  • c++
  • python
  • go
  • rust
  • typescript
• 原题传送门：https://leetcode-cn.com/problems/range-sum-of-bst/

---

二叉搜索树的范围和：

给定二叉搜索树的根结点 root，返回值位于范围 [low, high] 之间的所有结点的值的和。

样例 1：

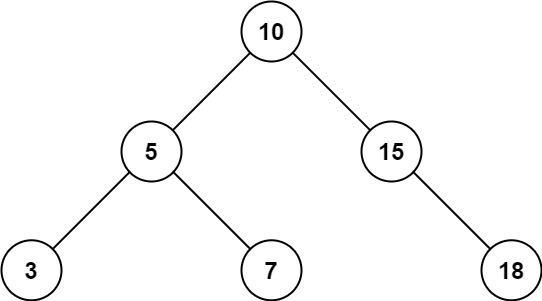
输入：
	root = [10,5,15,3,7,null,18], low = 7, high = 15
	
输出：
	32

样例 2：

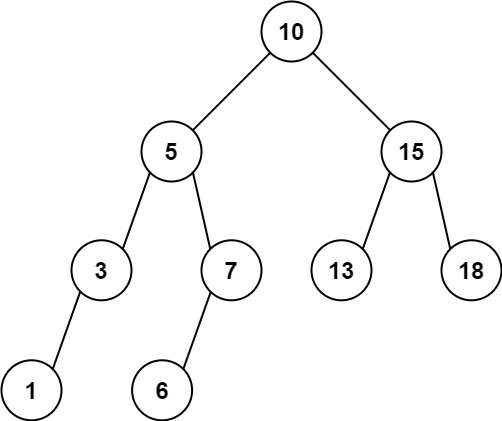
输入：
	root = [10,5,15,3,7,13,18,1,null,6], low = 6, high = 10
	
输出：
	23

提示：

• 树中节点数目在范围 [1, 2 * $10^4$] 内
• 1 <= Node.val <= $10^5$
• 1 <= low <= high <= $10^5$
• 所有 Node.val 互不相同

---

分析

• 面对这道算法题目，二当家的陷入了沉思。
• 遍历二叉搜索树是必然的，递归是最直观的方式。

---

题解

java

/**
 * Definition for a binary tree node.
 * public class TreeNode 
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() 
 *     TreeNode(int val)  this.val = val; 
 *     TreeNode(int val, TreeNode left, TreeNode right) 
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     
 * 
 */
class Solution 
    public int rangeSumBST(TreeNode root, int low, int high) 
        if (root == null) 
			return 0;
		
		int val;
		if (root.val >= low
			&& root.val <= high) 
			// 根结点符合条件
			val = root.val;
		 else 
			val = 0;
		
		int leftVal;
		if (root.val > low) 
			// 左子树可能大于等于low
			leftVal = rangeSumBST(root.left, low, high);
		 else 
			leftVal = 0;
		
		int rightVal;
		if (root.val < high) 
			// 右子树可能小于等于high
			rightVal = rangeSumBST(root.right, low, high);
		 else 
			rightVal = 0;
		
		return val + leftVal + rightVal;
    

---

c

/**
 * Definition for a binary tree node.
 * struct TreeNode 
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * ;
 */


int rangeSumBST(struct TreeNode* root, int low, int high)
    if (root == NULL) 
        return 0;
    
    int val;
    if (root->val >= low
        && root->val <= high) 
        // 根结点符合条件
        val = root->val;
     else 
        val = 0;
    
    int leftVal;
    if (root->val > low) 
        // 左子树可能大于等于low
        leftVal = rangeSumBST(root->left, low, high);
     else 
        leftVal = 0;
    
    int rightVal;
    if (root->val < high) 
        // 右子树可能小于等于high
        rightVal = rangeSumBST(root->right, low, high);
     else 
        rightVal = 0;
    
    return val + leftVal + rightVal;

---

c++

/**
 * Definition for a binary tree node.
 * struct TreeNode 
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) 
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) 
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) 
 * ;
 */
class Solution 
public:
    int rangeSumBST(TreeNode* root, int low, int high) 
        if (root == nullptr) 
            return 0;
        
        int val;
        if (root->val >= low
            && root->val <= high) 
            // 根结点符合条件
            val = root->val;
         else 
            val = 0;
        
        int leftVal;
        if (root->val > low) 
            // 左子树节点可能大于等于low
            leftVal = rangeSumBST(root->left, low, high);
         else 
            leftVal = 0;
        
        int rightVal;
        if (root->val < high) 
            // 右子树节点可能小于等于high
            rightVal = rangeSumBST(root->right, low, high);
         else 
            rightVal = 0;
        
        return val + leftVal + rightVal;
    
;

---

python

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def rangeSumBST(self, root: TreeNode, low: int, high: int) -> int:
        if root is None:
            return 0
        val = 0
        if root.val >= low and root.val <= high:
            # 根结点符合条件
            val = root.val
        left_val = 0
        if root.val > low:
            # 左子树可能大于等于low
            left_val = self.rangeSumBST(root.left, low, high)
        right_val = 0
        if root.val < high:
            # 右子树可能小于等于high
            right_val = self.rangeSumBST(root.right, low, high)
        return val + left_val + right_val
        

---

go

/**
 * Definition for a binary tree node.
 * type TreeNode struct 
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * 
 */
func rangeSumBST(root *TreeNode, low int, high int) int 
    if root == nil 
		return 0
	
	val := 0
	if root.Val >= low && root.Val <= high 
		// 根结点符合条件
		val = root.Val
	
	leftVal := 0
	if root.Val > low 
		// 左子树可能大于等于low
		leftVal = rangeSumBST(root.Left, low, high)
	
	rightVal := 0
	if root.Val < high 
		// 右子树可能小于等于high
		rightVal = rangeSumBST(root.Right, low, high)
	
	return val + leftVal + rightVal

---

rust

// Definition for a binary tree node.
// #[derive(Debug, PartialEq, Eq)]
// pub struct TreeNode 
//   pub val: i32,
//   pub left: Option<Rc<RefCell<TreeNode>>>,
//   pub right: Option<Rc<RefCell<TreeNode>>>,
// 
//
// impl TreeNode 
//   #[inline]
//   pub fn new(val: i32) -> Self 
//     TreeNode 
//       val,
//       left: None,
//       right: None
//     
//   
// 
use std::rc::Rc;
use std::cell::RefCell;
impl Solution 
    pub fn range_sum_bst(root: Option<Rc<RefCell<TreeNode>>>, low: i32, high: i32) -> i32 
        match root 
            Some(root) => 
                let mut root = root.borrow_mut();
                let val = if root.val >= low && root.val <= high 
                    root.val
                 else 
                    0
                ;
                let leftVal = if root.val > low 
                    Self::range_sum_bst(root.left.take(), low, high)
                 else 
                    0
                ;
                let rightVal = if root.val < high 
                    Self::range_sum_bst(root.right.take(), low, high)
                 else 
                    0
                ;
                val + leftVal + rightVal
            ,
            _ => 0
        
    

---

typescript

/**
 * Definition for a binary tree node.
 * class TreeNode 
 *     val: number
 *     left: TreeNode | null
 *     right: TreeNode | null
 *     constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) 
 *         this.val = (val===undefined ? 0 : val)
 *         this.left = (left===undefined ? null : left)
 *         this.right = (right===undefined ? null : right)
 *     
 * 
 */

function rangeSumBST(root: TreeNode | null, low: number, high: number): number 
    if (!root) 
        return 0;
    
    let val = 0;
    if (root.val >= low && root.val <= high) 
        // 根结点符合条件
        val = root.val;
    
    let leftVal = 0
    if (root.val > low) 
        // 左子树可能大于等于low
        leftVal = rangeSumBST(root.left, low, high);
    
    let rightVal = 0;
    if (root.val < high) 
        // 右子树可能小于等于high
        rightVal = rangeSumBST(root.right, low, high);
    
    return val + leftVal + rightVal;
;

---

原题传送门：https://leetcode-cn.com/problems/range-sum-of-bst/

---

非常感谢你阅读本文~
欢迎【👍点赞】【⭐收藏】【📝评论】~
放弃不难，但坚持一定很酷~
希望我们大家都能每天进步一点点~
本文由 二当家的白帽子：https://le-yi.blog.csdn.net/ 博客原创~

---