Q:给定一个二叉搜索树,同时给定最小边界L 和最大边界 R。通过修剪二叉搜索树,使得所有节点的值在[L, R]中 (R>=L) 。你可能需要改变树的根节点,所以结果应当返回修剪好的二叉搜索树的新的根节点。

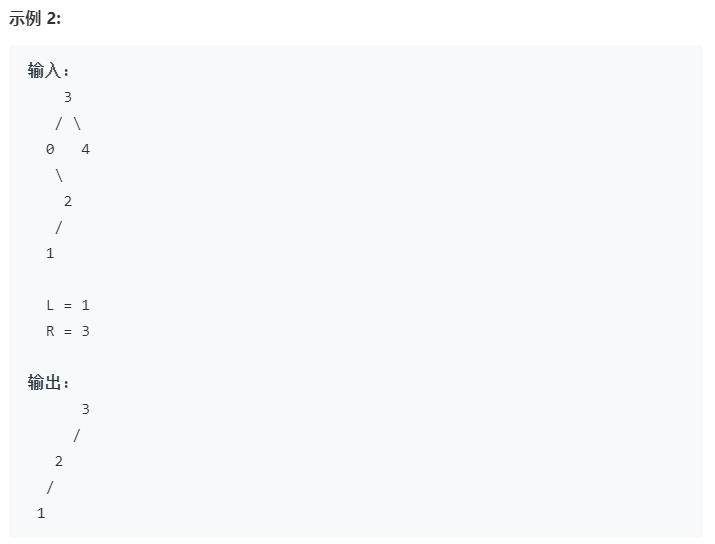
A:
思路分析:
- 修剪一棵树,如果根结点的值小于给定的左边界L,那么当前结点及其左子树就会被修剪掉,修剪后的树应该是其右子树,但是右子树不一定是符合范围的树,所以要对其右子树叶进行修剪,然后返回修剪后的右子树。
- 同理,根结点的值大于给定的右边界R,修剪后的树应该是其左子树且要对左子树修剪。
- 涉及到改变树的结构,就需要更新链接,如果当前结点值在范围内,那么修建其左右子树,并且更新左右链接。最后将当前修剪好的子树返回。
时间复杂度为O(n), 空间复杂度与树高成正比。
代码:
public TreeNode trimBST(TreeNode root, int L, int R) {
if (root == null)
return null;
if (root.val < L)
return trimBST(root.right, L, R);
if (root.val > R)
return trimBST(root.left, L, R);
root.left = trimBST(root.left, L, R);
root.right = trimBST(root.right, L, R);
return root;
}