A*路径搜索算法基于A星的最优避障路径搜索算法的MATLAB仿真+GUI界面

Posted 2022-04-13 fpga&matlab

1.软件版本

MATLAB2021a

2.基本原理

A算法是启发式算法重要的一种，主要是用于在两点之间选择一个最优路径，而A的实现也是通过一个估值函数

F=G+H

• G表示该点到起始点位所需要的代价
• H表示该点到终点的曼哈顿距离。
• F就是G和H的总和，而最优路径也就是选择最小的F值，进行下一步移动（后边会做详细介绍）

3.核心代码

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%Author:Michael Jacob Mathew

% The following code illustrates the A star search algorithm.
% The code is self explanatory
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

% clc; clear all; clear classes;
function [PathTake, Found]=A_Star_Search(grid,init,goal)
tic;
cost=1;
Found=false;
Resign=false;

% grid=NewGrid();
% 
% init = [1,1]; %Start
% goal = [size(grid,1), size(grid,2)]; % Goal.

Heuristic=CalculateHeuristic(grid,goal); %Calculate the Heuristic   
 
ExpansionGrid(1:size(grid,1),1:size(grid,2)) = -1; % to show the path of expansion

ActionTaken=zeros(size(grid)); %Matrix to store the action taken to reach that particular cell

OptimalPath(1:size(grid,1),1:size(grid,2))=' '; %Optimal Path derived from A Star

%how to move in the grid

delta = [-1,  0; % go up
          0, -1; % go left
          1,  0; %go down
          0,  1]; % go right
%           1,  1; %diagonal down
%          -1, -1]; %diagonal up
 

 
 for i=1:size(grid,1)
     for j=1:size(grid,2)
         gridCell=search();
         if(grid(i,j)>0)
            gridCell=gridCell.Set(i,j,1,Heuristic(i,j));
         else
             gridCell=gridCell.Set(i,j,0,Heuristic(i,j));
         end
         GRID(i,j)=gridCell;
         clear gridCell;
     end
 end

% drawEnvironment(grid,init,goal);

Start=search();
Start=Start.Set(init(1),init(2),grid(init(1),init(2)),Heuristic(init(1),init(2)));
Start.isChecked=1;
GRID(Start.currX,Start.currY).isChecked=1;
Goal=search();
Goal=Goal.Set(goal(1),goal(2),grid(goal(1),goal(2)),0);
 
OpenList=[Start];
ExpansionGrid(Start.currX,Start.currY)=0;

small=Start.gValue+Start.hValue;

count=0;
 while(Found==false || Resign==false) 
    
 small=OpenList(1).gValue+OpenList(1).hValue+cost;

for i=1:size(OpenList,2)
        fValue=OpenList(i).gValue+OpenList(i).hValue;
        if(fValue<=small)
            small=fValue;
            ExpandNode=OpenList(i);
            OpenListIndex=i;
        end
    end
    
   
    OpenList(OpenListIndex)=[];

    
    ExpansionGrid(ExpandNode.currX,ExpandNode.currY)=count;
    count=count+1;
    
    for i=1:size(delta,1)
        direction=delta(i,:);
        if(ExpandNode.currX+ direction(1)<1 || ExpandNode.currX+direction(1)>size(grid,1)|| ExpandNode.currY+ direction(2)<1 || ExpandNode.currY+direction(2)>size(grid,2))
            continue;
        else
            NewCell=GRID(ExpandNode.currX+direction(1),ExpandNode.currY+direction(2));
            
             if(NewCell.isChecked~=1 && NewCell.isEmpty~=1)
                GRID(NewCell.currX,NewCell.currY).gValue=GRID(ExpandNode.currX,ExpandNode.currY).gValue+cost;
                GRID(NewCell.currX,NewCell.currY).isChecked=1; %modified line from the v1
                OpenList=[OpenList,GRID(NewCell.currX,NewCell.currY)]; 
                ActionTaken(NewCell.currX,NewCell.currY)=i;
             end
            
             if(NewCell.currX==Goal.currX && NewCell.currY==Goal.currY && NewCell.isEmpty~=1)
                Found=true;
                Resign=true;
                disp('Search Successful');
                GRID(NewCell.currX,NewCell.currY).isChecked=1;
                ExpansionGrid(NewCell.currX,NewCell.currY)=count;
                GRID(NewCell.currX,NewCell.currY);
                break;
            end
            
        end
    end

     if(isempty(OpenList) && Found==false)
         Resign=true;
         disp('Search Failed');
         break;
     end
 end
 PathTake=[]; %For stroring the values taken for the path.
 if(Found==true) %further process only if there is a path
     Policy='Up','Left','Down','Right','Diag Down','Diag Up';
     X=goal(1);Y=goal(2);
     OptimalPath(X,Y)='GOAL';
     while(X~=init(1)|| Y~=init(2))
         x2=X-delta(ActionTaken(X,Y),1);
         y2=Y-delta(ActionTaken(X,Y),2);
         OptimalPath(x2,y2)=Policy(ActionTaken(X,Y));
         PathTake=[PathTake;[X,Y]];
         X=x2;
         Y=y2;
     end
     PathTake=[PathTake;[init(1),init(2)]]; % add the start state to the end
     Total_Elapsed_Time=toc

%     figure;
    plot(fliplr((PathTake(:,2))'),fliplr((PathTake(:,1))'));
    set(gca,'XLim',[-1,size(grid,2)+2],'YLim',[-1,size(grid,1)+2]);
    set(gca,'YDir','reverse');

   % SmoothPath(PathTake,size(grid));

%  ExpansionGrid; %to see how the expansion took place
%     OptimalPath %to see the optimal path taken by the Search Algo
 else

     disp('No Path to Display');
     Total_Elapsed_Time=toc
 end
end

4.操作步骤与仿真结论

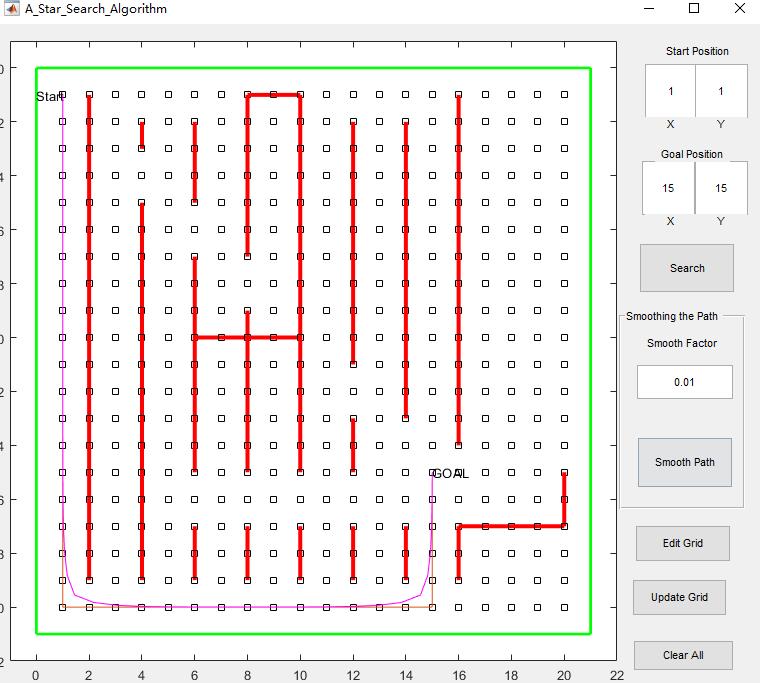
5.参考文献

[1]张海涛, 程荫杭. 基于A*算法的全局路径搜索[J]. 微计算机信息, 2007(17):3.

D217

6.完整源码获得方式

方式1：微信或者QQ联系博主

方式2：订阅MATLAB/FPGA教程，免费获得教程案例以及任意2份完整源码