算法 | A*算法实现最优路径规划

Posted 2022-08-05 TiAmo zhang

 启发式探索是利用问题拥有的启发信息来引导搜索，达到减少探索范围、降低问题复杂度的目的。A*寻路算法是启发式探索的一个典型实践，在寻路搜索的过程中，给每个节点绑定了一个估计值(即启发式)，在对节点的遍历过程中采取估计值优先原则，估计值更优的节点会被优先遍历。

1、A*算法基本原理

A*算法是一种有序搜索算法，其特点在于对估价函数的定义上。公式表示为：  f(n)=g(n)+h(n)，其中， f(n)是从初始状态经由状态n到目标状态的代价估计，g(n) 是在状态空间中从初始状态到状态n的实际代价，h(n)是从状态n到目标状态的最佳路径的估计代价。对于路径搜索问题，状态就是图中的节点，代价就是距离。

2、A*算法搜索步骤

1. 算法步骤

(1) 设置地图大小，起点S，终点E，障碍集合Blocklist。

(2) 添加起点S到Openlist(待搜索集合)。

(3) 将S取出，添加到Closelist(已搜索集合)。

(4) 查找S所有相邻节点，添加到Openlist，并设置S为它们的父节点；以绿色初始节点右侧的灰色节点为例：f(n)=g(n)+h(n)。g(n)=1,绿色初始节点到该节点的移动步数；h(n)=3,灰色节点移动到红色终点的步数(曼哈顿距离)，也可以使用欧氏距离。f(n)=g(n)+h(n)=1+3=4,其他相邻节点计算相同。如图1所示，曼哈顿距离向4个方向移动，距离公式为：

欧氏距离向8个方向移动，距离公式为：

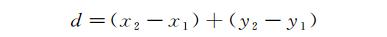
■ 图 1步骤(4)示意图

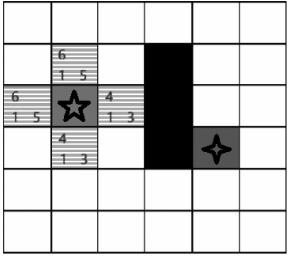
(5) 选择Openlist中f值最小点，有两个分别为绿色右侧节点和绿色下方节点，将右侧节点添加至Closelist，并设置绿色节点为其父节点，选择下方节点也可以，本例节点顺序右下左上，根据启发式规则相同，结果和搜索效率与选取顺序无关,如图2所示。

■ 图2 步骤(5)示意图

(6) 此时Openlist中f的最小值是4，黄色相邻节点中只有上下节点可达，根据计算得到上下节点f值，此处f值为最小值，采用其他路径计算值均不小于4,如图3所示。

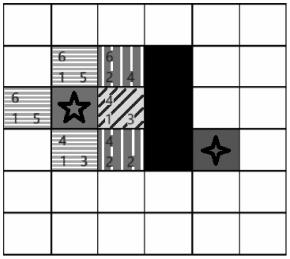
■ 图3 黄色相邻上下节点

因此，选取黄色节点下方f值小的节点添加至Closelist，此时Openlist中f的最小值为4，继续选取节点添加至Openlist,如图4所示。

■ 图4 步骤(6)示意图

接下来算法进入相同方式迭代过程。

A*算法最终执行结果如图5所示。

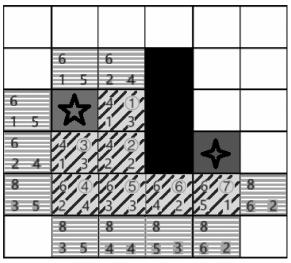
■ 图5 结果示意图

2. 路径搜索

开始从红色节点逆推，红色节点的父节点为⑦号节点，⑦号节点的父节点为⑥号节点，⑥号节点的父节点为⑤号节点，⑤号节点的父节点为②号节点，⑤号节点是搜索到②号节点时添加到Openlist中的，并且一直未被更新，②号节点的父节点为①号节点，最终的搜索路径为：起点-①-②-⑤-⑥-⑦-终点。

这里的搜索路径并不是最佳路径的唯一解，其中路径：起点-③-④-⑤-⑥-⑦和路径：起点-③-②-⑤-⑥-⑦都可以通过相应的算法求出，作为搜索的最佳路径，因为这些路径理论上是等同的，这里只以一种最佳路径作为演示。

对于上例演示的情况中存在无论如何重新计算Openlist中节点的f值都不会更小，也就是无法进行更新操作，因此再举一个例子，演示更新搜索。

现在考虑可以8个方向搜索，但是斜向搜索需要步数为4。

选择Openlist中f值最小的节点，选择了右侧f值为4的节点，此时计算右侧f值为4的节点的相邻节点的f值，如图6所示。其中左侧绿色起始点已经添加进Closelist中，右侧三个为黑色节点，因此不考虑这4个节点，其他节点均已存在于Openlist中，现对其f值进行更新。

(1) 先看左上角的相邻节点，通过黄色节点到达该节点，g(n) = 5，h(n)不变，f(n)反而更大了，因此不更新。左下角节点同理。

(2) 上方节点，通过黄色节点计算g(n) = 2, h(n)不变，f(n) = 6 < 8。所以，更新这个节点的f值，并将其父节点修改为黄色节点。下方居中节点同理,如图7所示。

 

3、使用Python实现上述流程

(1) 绘制地图全貌：起点、终点、障碍和可通行节点。

(2) 获得相邻节点。

(3) 采用曼哈顿或欧氏距离计算h(n)。

(4) 更新f值。

(5) 绘制搜索最优路径

 

4、最优路径规划

尝试采用A*算法对图8所示的地图进行最优路径规划。

■ 图8 路径规划图

附录B A*算法实现最优路径规划

(1) 已搜索的③号节点邻居节点添加至Openlist，Openlist中f最小值为6，根据右下左上顺序原则优先选取下方节点，如图B.1所示。

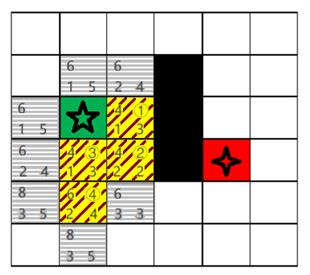
附B.1 Step7示意图

(2) 此时④号节点邻居节点添加至Openlist，Openlist中f最小值为6，根据右下左上顺序原则，优先选取右侧节点，如图B.2所示。

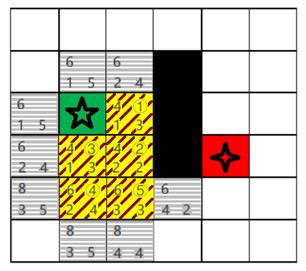
附B.2  Step8示意图

(3) 此时Openlist中f最小值为6，选择⑤号节点的右侧节点添加至Closelist，如图B.3所示。

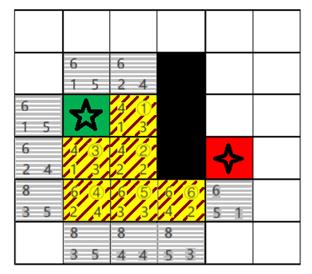
附B.3  Step9示意图

(4) 选取⑥号节点右侧节点添加到Closelist，此时Openlist中已包含了红色终止节点，算法结束，如图B.4所示。

附B.4  Step10示意图

算法示例程序：

import math
from random import randint
import pygame
from enum import Enum

# 定义全局变量：地图中节点的像素大小
CELL_WIDTH = 30 #单元格宽度
CELL_HEIGHT = 30 #单元格长度
BORDER_WIDTH = 1 #边框宽度
BLOCK_NUM = 3 #地图中的障碍物数量

class Color(Enum):
    ''' 颜色 '''
    RED = (255, 0, 0)
    GREEN = (0, 255, 0)
    BLUE = (0, 0, 255)
    WHITE = (255, 255, 255)
    BLACK = (0, 0, 0)
    GREY=(128,128,128)

    @staticmethod
    def random_color():
        '''设置随机颜色'''
        r = randint(0, 255)
        g = randint(0, 255)
        b = randint(0, 255)
        return (r, g, b)

class Map(object):
    def __init__(self, mapsize):
        self.mapsize = mapsize

    def generate_cell(self, cell_width, cell_height):
        '''
        定义一个生成器，用来生成地图中的所有节点坐标
        :param cell_width: 节点宽度
        :param cell_height: 节点长度
        :return: 返回地图中的节点
        '''
        x_cell = -cell_width
        for num_x in range(self.mapsize[0] // cell_width):
            y_cell = -cell_height
            x_cell += cell_width
            for num_y in range(self.mapsize[1] // cell_height):
                y_cell += cell_height
                yield (x_cell, y_cell)

class Node(object):
    def __init__(self, pos):
        self.pos = pos
        self.father = None
        self.gvalue = 0
        self.fvalue = 0

    def compute_fx(self, enode, father):
        if father == None:
            print('未设置当前节点的父节点！')

        gx_father = father.gvalue
        #采用欧氏距离计算父节点到当前节点的距离
        #gx_f2n = math.sqrt((father.pos[0] - self.pos[0])**2 + (father.pos[1] - self.pos[1])**2)
        gx_f2n = abs(father.pos[0] - self.pos[0]) + abs(father.pos[1] - self.pos[1])
        gvalue = gx_f2n + gx_father

        #hx_n2enode = math.sqrt((self.pos[0] - enode.pos[0])**2 + (self.pos[1] - enode.pos[1])**2)
        hx_n2enode = abs(self.pos[0] - enode.pos[0])+ abs(self.pos[1] - enode.pos[1])
        fvalue = gvalue + hx_n2enode
        return gvalue, fvalue

    def set_fx(self, enode, father):
        self.gvalue, self.fvalue = self.compute_fx(enode, father)
        self.father = father

    def update_fx(self, enode, father):
        gvalue, fvalue = self.compute_fx(enode, father)
        if fvalue < self.fvalue:
            self.gvalue, self.fvalue = gvalue, fvalue
            self.father = father

class AStar(object):
    def __init__(self, mapsize, pos_sn, pos_en):
        self.mapsize = mapsize #表示地图的投影大小，并非屏幕上的地图像素大小
        self.openlist, self.closelist, self.blocklist = [], [], []
        self.snode = Node(pos_sn) #用于存储路径规划的起始节点
        self.enode = Node(pos_en) #用于存储路径规划的目标节点
        self.cnode = self.snode #用于存储当前搜索到的节点

    def run(self):
        self.openlist.append(self.snode)
        while(len(self.openlist) > 0):
            #查找openlist中fx最小的节点
            fxlist = list(map(lambda x: x.fvalue, self.openlist))
            index_min = fxlist.index(min(fxlist))
            self.cnode = self.openlist[index_min]
            del self.openlist[index_min]
            self.closelist.append(self.cnode)

            # 扩展当前fx最小的节点，并进入下一次循环搜索
            self.extend(self.cnode)
            # 如果openlist列表为空，或者当前搜索节点为目标节点，则跳出循环
            if len(self.openlist) == 0 or self.cnode.pos == self.enode.pos:
                break

        if self.cnode.pos == self.enode.pos:
            self.enode.father = self.cnode.father
            return 1
        else:
            return -1

    def get_minroute(self):
        minroute = []
        current_node = self.enode

        while(True):
            minroute.append(current_node.pos)
            current_node = current_node.father
            if current_node.pos == self.snode.pos:
                break

        minroute.append(self.snode.pos)
        minroute.reverse()
        return minroute

    def extend(self, cnode):
        nodes_neighbor = self.get_neighbor(cnode)
        for node in nodes_neighbor:
            #判断节点node是否在closelist和blocklist中，因为closelist和blocklist中元素均为Node类，所以要用map函数转换为坐标集合
            if node.pos in list(map(lambda x:x.pos, self.closelist)) or node.pos in self.blocklist:
                continue
            else:
                if node.pos in list(map(lambda x:x.pos, self.openlist)):
                    node.update_fx(self.enode, cnode)
                else:
                    node.set_fx(self.enode, cnode)
                    self.openlist.append(node)

    def setBlock(self, blocklist):
        '''
        获取地图中的障碍物节点，并存入self.blocklist列表中
        注意：self.blocklist列表中存储的是障碍物坐标，不是Node类
        :param blocklist:
        :return:
        '''
        self.blocklist.extend(blocklist)

    def get_neighbor(self, cnode):
        #offsets = [(-1,1),(0,1),(1,1),(-1,0),(1,0),(-1,-1),(0,-1),(1,-1)]
        offsets = [(-1, 0), (1, 0), (0, 1), (0, -1)]
        nodes_neighbor = []
        x, y = cnode.pos[0], cnode.pos[1]
        for os in offsets:
            x_new, y_new = x + os[0], y + os[1]
            pos_new = (x_new, y_new)
            #判断是否在地图范围内,超出范围跳过
            if x_new < 0 or x_new > self.mapsize[0] - 1 or y_new < 0 or y_new > self.mapsize[1]:
                continue
            nodes_neighbor.append(Node(pos_new))

        return nodes_neighbor


def main():
    mapsize = tuple(map(int, input('请输入地图大小，以逗号隔开：').split(',')))
    pos_snode = tuple(map(int, input('请输入起点坐标，以逗号隔开：').split(',')))
    pos_enode = tuple(map(int, input('请输入终点坐标，以逗号隔开：').split(',')))
    myAstar = AStar(mapsize, pos_snode, pos_enode)
    blocklist = gen_blocks(mapsize[0], mapsize[1])
    myAstar.setBlock(blocklist)
    routelist = [] #记录搜索到的最优路径
    if myAstar.run() == 1:
        routelist = myAstar.get_minroute()
        print(routelist)
        showresult(mapsize, pos_snode, pos_enode, blocklist, routelist)
    else:
        print('路径规划失败！')

def gen_blocks(width, height):
    '''
    随机生成障碍物
    :param width: 地图宽度
    :param height: 地图高度
    :return:返回障碍物坐标集合
    '''
    i, blocklist = 0, []
    while(i < BLOCK_NUM):
        for j in range(3):
            block = (3, j+1)
            if block not in blocklist:
                blocklist.append(block)
                i+=1
    return blocklist

def showresult(mapsize, pos_sn, pos_en, blocklist, routelist):
    # 初始化导入的Pygame模块
    pygame.init()
    # 此处要将地图投影大小转换为像素大小，此处设地图中每个单元格的大小为CELL_WIDTH*CELL_HEIGHT像素
    mymap = Map((mapsize[0]*CELL_WIDTH, mapsize[1]*CELL_HEIGHT))
    pix_sn = (pos_sn[0]*CELL_WIDTH, pos_sn[1]*CELL_HEIGHT)
    pix_en = (pos_en[0]*CELL_WIDTH, pos_en[1]*CELL_HEIGHT)
    #对blocklist和routelist中的坐标同样要转换为像素值
    bl_pix = list(map(transform, blocklist))
    rl_pix = list(map(transform, routelist))
    # 初始化显示的窗口并设置尺寸
    screen = pygame.display.set_mode(mymap.mapsize)
    # 设置窗口标题
    pygame.display.set_caption('A*算法路径搜索演示：')
    #用白色填充屏幕
    screen.fill(Color.WHITE.value)

    #绘制屏幕中的所有单元格
    for (x, y) in mymap.generate_cell(CELL_WIDTH, CELL_HEIGHT):
        if (x,y) in bl_pix:
            #绘制黑色的障碍物单元格，并留出2个像素的边框
            pygame.draw.rect(screen, Color.BLACK.value, ((x+BORDER_WIDTH,y+BORDER_WIDTH), (CELL_WIDTH-2*BORDER_WIDTH, CELL_HEIGHT-2*BORDER_WIDTH)))
        else:
            # 绘制绿色的可通行单元格，并留出2个像素的边框
            pygame.draw.rect(screen, Color.GREEN.value, ((x+BORDER_WIDTH,y+BORDER_WIDTH), (CELL_WIDTH-2*BORDER_WIDTH, CELL_HEIGHT-2*BORDER_WIDTH)))
    #绘制起点和终点
    pygame.draw.circle(screen, Color.BLUE.value, (pix_sn[0]+CELL_WIDTH//2, pix_sn[1]+CELL_HEIGHT//2), CELL_WIDTH//2 - 1)
    pygame.draw.circle(screen, Color.RED.value, (pix_en[0]+CELL_WIDTH//2, pix_en[1]+CELL_HEIGHT//2), CELL_WIDTH//2 - 1)

    #绘制搜索得到的最优路径
    for (x, y) in mymap.generate_cell(CELL_WIDTH, CELL_HEIGHT):
        if (x,y) in rl_pix and (x,y)!=(pix_sn[0],pix_sn[1]) and (x,y)!=(pix_en[0],pix_en[1]):
            pygame.draw.rect(screen, Color.GREY.value, ((x+BORDER_WIDTH,y+BORDER_WIDTH), (CELL_WIDTH-2*BORDER_WIDTH, CELL_HEIGHT-2*BORDER_WIDTH)))
    #pygame.draw.aalines(screen, Color.RED.value, False, rl_pix)
    keepGoing = True
    while keepGoing:
        pygame.time.delay(100)
        for event in pygame.event.get():
            if event.type == pygame.QUIT:
                keepGoing = False
        pygame.display.flip()

def transform(pos):
    xnew, ynew = pos[0]*CELL_WIDTH, pos[1]*CELL_HEIGHT
    return (xnew, ynew)

if __name__ == '__main__':
    main()