机器学习学习整理前言与线性回归

Posted 2022-04-04 冬阳thu

---

文章目录

• 前言
• 一、简短的预备知识
• 二、线性回归
• • 数学推导：
  • 基于numpy实现线性回归
• 总结

前言

博主是一名普通的EE大三学生，专业分流在电子-生医院系，因为实验和工作需要，目前在自学deep learning，开这个专栏为了用自己的数学知识来解释一些公式推导，巩固自己的知识基础，也希望（可能会）帮到同样在学习的同学。
有任何想法或指正都清不吝赐教，希望和大家共同学习

ps.
1 由于这是作为知识拆解&名词解释，便跳过DeepLearning的历史内容基本意义等知识
2 之前有幸在老师实验室做了linux可视化相关的工作（项目还没完全完成，等做完发出来请大家提供意见）后续我会整理在做这个的时候遇到的问题以及个人见解分享出来（主要是关于linux、python、mayavi、vtk、mne）
3 本文大体参照鲁伟老师的

---

一、简短的预备知识

基础名词

训练集：用于训练机器学习模型
测试集：用于测试学习模型对未知数据的成绩/效果

有标签：分类问题，回归问题–>监督学习
（预期的值是离散的–>分类问题）
（预期的值是连续的–>回归问题）

没有特定标签：聚类–>无监督学习

机器学习三要素

模型（model）
策略（strategy）
算法（algorithm）

（这里的算法指确定模型和损失函数后，把机器学习的过程转化为一个最优化问题，在优化时使用的优化算法）

二、线性回归

数学推导：

上文有提到回归问题是来解决有标签，目标值为连续的学习模型，
我们的目的是通过一组输入的数据集，将一些特定的属性（标签/特征）等影响输入值的因素作为x，输出值为y，建立y=wx+b的的模型，
在线性回归中采用均方误差最小化来描述模型准确性的方法，因此：
我们要确定参数w和b来使我们学习模型求得的y趋近于真实的y，也就是使拟合输出和真实输出间均方误差最小，
也就是：

为了求得w，b的最小化参数，我们基于上式，分别对w，b求偏导，
……（）偏导过程略）
得到：

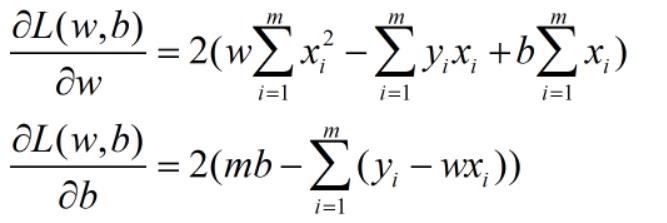
分别令其=0，解得：

（书中也有提到，这其实就是最小二乘法，帮助大家回顾一下大一知识hhh）

在了解到最小二乘就是建模线性回归的本质后，我们只需要向里面添加更多的“标签”，在数学上也就是变为矩阵运算；

w的计算变为了向量计算：

到这里我们便完成了数学推导的部分，接下来就是将数学语言变成代码（基于numpy）
我们可以看到其实线性回归自身的思想很简单，无非是用最小二乘的方法不断的去逼向一个个输入点，最后使均方差最小。

基于numpy实现线性回归

没来得及做详细注释，有任何问题可以私信讨论
训练部分：
回归主体函数，初始化函数，训练过程函数

import numpy as np


def linear_loss(X, y, w, b):
	num_train = X.shape[0]
	num_feature = X.shape[1]
	y_hat = np.dot(X, w) + b
	loss = np.sum((y_hat - y) ** 2) / num_train
	dw = np.dot(X.T, (y_hat - y)) / num_train
	db = np.sum((y_hat - y)) / num_train
	return y_hat, dw, db


def initail(dims):
	w = np.zeros((dims, 1))
	b = 0
	return w, b


def linear_train(X, y, learningrate=0.01, epochs=10000):
	loss_his = []
	w, b = initail(X.shape[1])
	for i in range(1, epochs):
		y_hat, loss, dw, db = linear_loss(X, y, w, b)
		w += -learningrate * dw
		b += -learningrate * db
		loss_his.append(loss)
		if i % 10000 == 0
			print('epoch %d loss %f' % (i, loss))
		grads = 
			'dw': dw, 'db': db
		
		params = 
			'w': w, 'b': b
		
	return loss_his, params, grads

---

总结

后续章节：

• 对数几率回归
• 聚类分析与k均值聚类算法
• 主成分分析
• 贝叶斯概率模型

希望对您有帮助~

冬阳