三天爆肝快速入门机器学习:线性回归逻辑回归岭回归第三天
Posted 普通网友
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了三天爆肝快速入门机器学习:线性回归逻辑回归岭回归第三天相关的知识,希望对你有一定的参考价值。
三天爆肝快速入门机器学习【第三天】
前言:这个系列终于写完了,只写了三篇,但是基础知识基本都写了,但是阅读量都不高,可能也是自己初次写这种系列的没什么经验,排版内容都有很大改进的空间,后面会出基础内容的系列和面试题这块的讲解,主要更新这两个内容,同时也会出视频讲解,这样的话比看文章更容易理解,码字不易,希望各位朋友给个三连,精彩内容持续更新中.
线性回归
优点
解决回归问题
思想简单,实现容易
许多强大的非线性模型的基础(多项式回归,逻辑回归,SVM)
结果具有很好的可解释性
蕴含机器学习中的很多重要思想
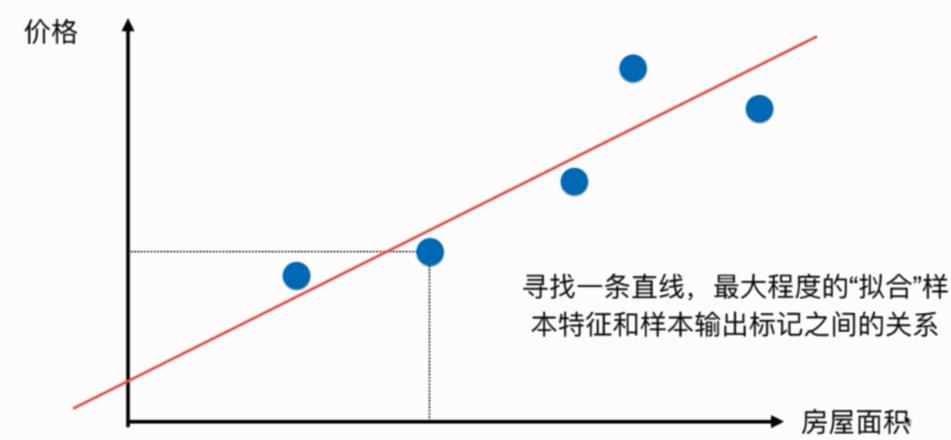
上一篇讲K近邻算法时,分类二维平面图横轴纵轴都是样本的特征
上图只有横轴是样本的特征,纵轴是样本的输出标记
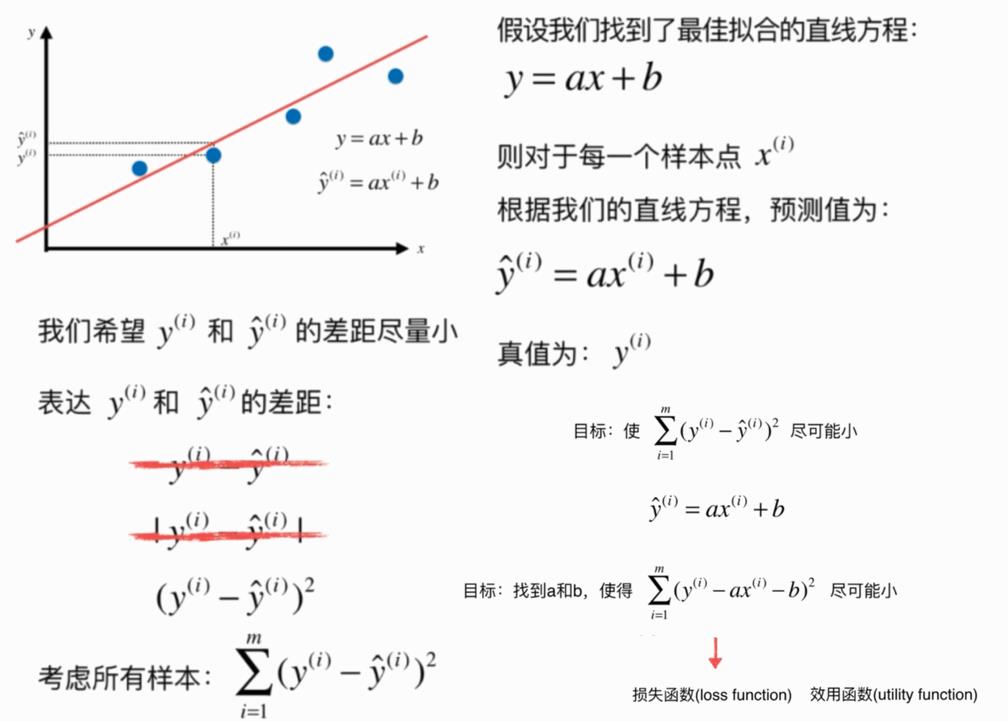
通过分析问题,确定问题的损失函数或者效用函数;
通过最优化损失函数或者效用函数,获得机器学习的模型。
近乎所有参数学习算法都是这样的套路(多项式回归,逻辑回归,SVM,神经网络)->学科:最优化原理->分支:凸优化
最小二乘法
典型的最小二乘法问题:最小化误差的平方
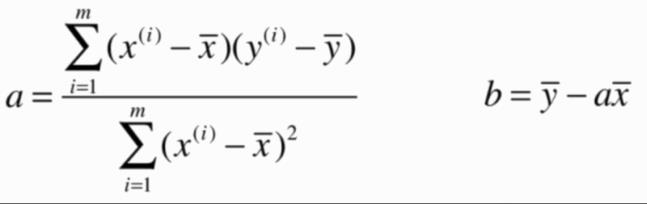

简单来说,就是求函数的极值,对函数各个未知分量求导,让导数等于零

向量化
提升大概五十倍的性能
x_mean = np.mean(x_train)
y_mean = np.mean(y_train)
num = 0.0
d = 0.0
for x,y in zip(x_train,y_train):
num += (x-x_mean) * (y - y_mean)
d += (x - x_mean) ** 2
self.a_ = num /d
self.b_ = y_mean - self.a_*x_mean
x_mean = np.mean(x_train)
y_mean = np.mean(y_train)
num = (x_train - x_mean).dot(y_train - y_mean)
d = (x_train - x_mean).dot(x_train - x_mean)
d = 0.0
self.a_ = num /d
self.b_ = y_mean - self.a_*x_mean
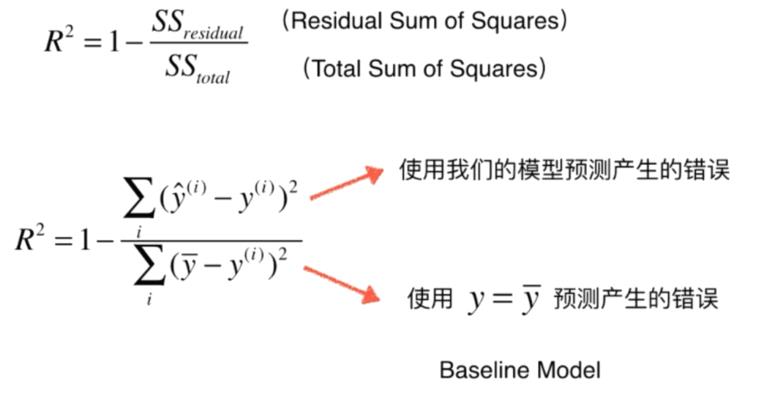
衡量指标 MSE,RMS,MAE



最好的指标 R Squared

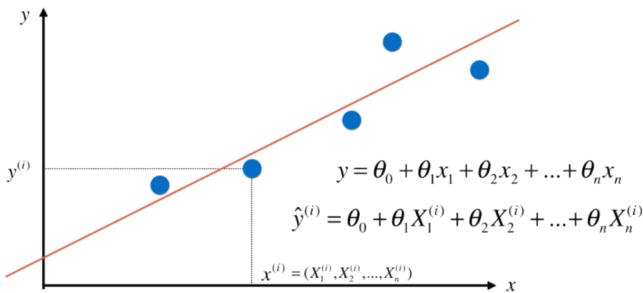
多元线性回归
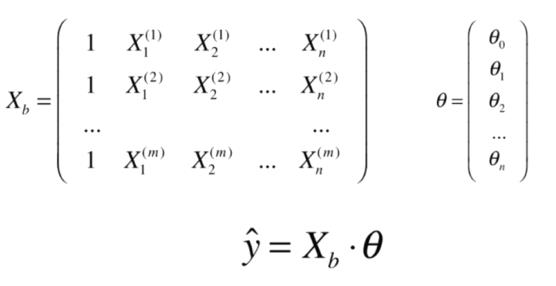

问题:时间复杂度高:O(n3)(优化O(n2.4)
优点:不需要对数据做归一化处理


过拟合和欠拟合
1 过拟合
过拟合的表现是模型在训练集上表现很好,在测试集上表现不好。样本集和整体数据集之间存在偏差,而过于复杂的模型可能对这个偏差也会进行拟合。
1.1 过拟合的原因
训练样本不足或缺乏代表性,没有涵盖所有数据类型。
训练数据中噪声过大。
模型过于复杂。
1.2 解决过拟合的方法
正则化,包括L1正则化、L2正则化
Dropout
Batch Normalization
early stopping
data augmentation
从简单的模型开始,而不是一开始就选择比较复杂的模型。
增加训练样本。
使用bagging方法。
降维。
2 欠拟合
欠拟合的表现是模型在训练集上的表现差,没有学习到数据的规律。
2.1 欠拟合的原因
模型过于简单。
特征数目太少。

2.2 解决欠拟合的方法
增加更多的特征。
增大模型复杂度。
使用boosting方法。
3 偏差和方差
可以从偏差和方差的角度理解过拟合和欠拟合。模型的泛化误差可以分为偏差和方差。设特征向量为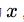
,目标函数为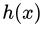
,拟合出来的函数为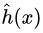
3.1 偏差(bias)
偏差是模型本身导致的误差,即错误的模型假设导致的误差。它表示预测结果的期望和真实值之间的差距,描述了算法的拟合能力。
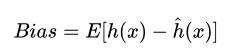
高偏差意味着模型的输出值和真实值之间的差距很大,故而会导致欠拟合问题。
3.2 方差(variance)
方差的出现是由于训练集中存在的一定程度的波动,可以理解为预测结果的波动程度,描述了数据扰动带来的影响。
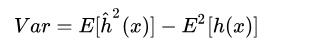
高方差意味着模型会对训练集中存在的噪声进行拟合,从而出现过拟合。
3.3 偏差-方差窘境
一般来说,偏差和方差是有冲突的。当模型的拟合能力不足时,训练数据的扰动不足以使模型的性能发生明显变化,此时偏差在总体误差中占据主导;随着模型拟合能力的上升,偏差越来越小,训练数据中存在的扰动会被模型学习到,故而方差逐渐占据主导。
3.4 方差和偏差的折中
模型的总体误差是偏差平方、方差和噪声之和(偏差-方差分解):
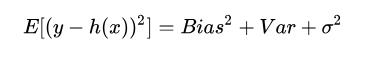
如果模型过于简单,一般会有大的偏差;如果模型过于复杂,会有大的方差和小的偏差。因此,一般需要在偏差和方差之间进行折中。一般情况下,交叉验证有助于这种折中。

岭回归
岭回归的概念
在进行特征选择时,一般有三种方式:
子集选择
收缩方式(Shrinkage method),又称为正则化(Regularization)。主要包括岭回归个lasso回归。
维数缩减
岭回归(Ridge Regression)是在平方误差的基础上增加正则项
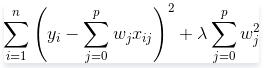
通过确定
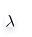
的值可以使得在方差和偏差之间达到平衡:随着
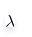
的增大,模型方差减小而偏差增大。
对
求导,结果为
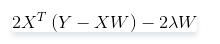
令其为0,可求得
的值:
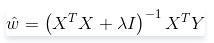
三、实验的过程
我们去探讨一下取不同的
对整个模型的影响。
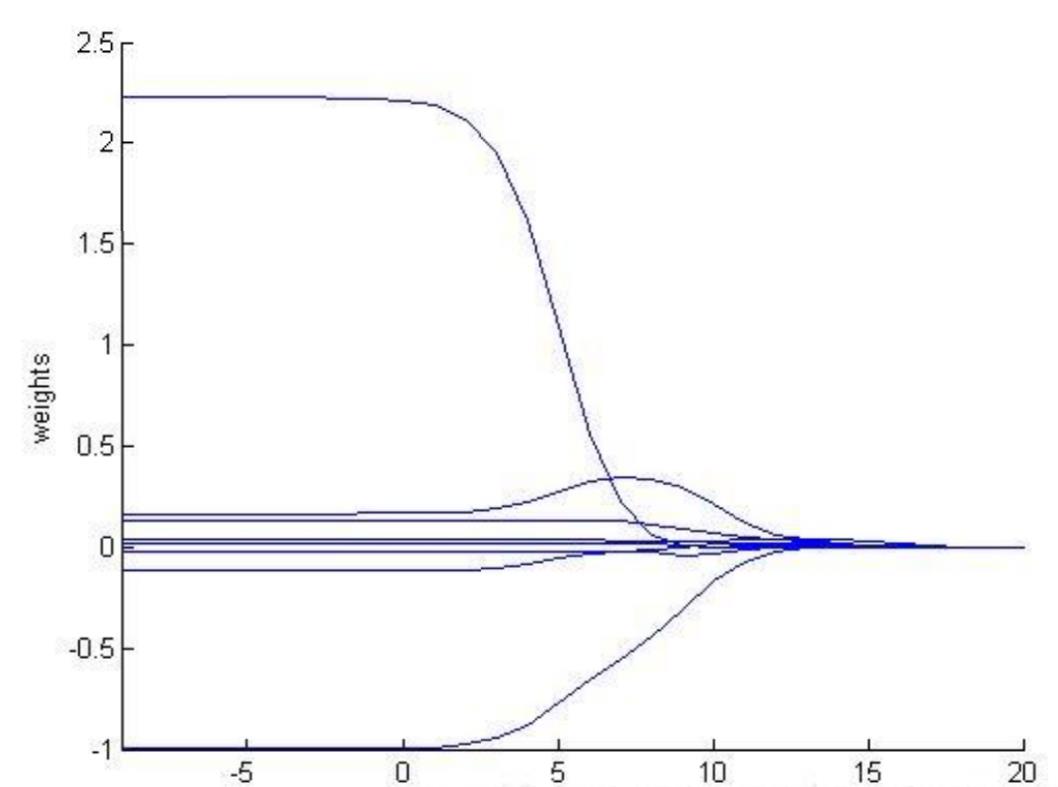
MATLAB代码
主函数
%% 岭回归(Ridge Regression)
%导入数据
data = load('abalone.txt');
[m,n] = size(data);
dataX = data(:,1:8);%特征
dataY = data(:,9);%标签
%标准化
yMeans = mean(dataY);
for i = 1:m
yMat(i,:) = dataY(i,:)-yMeans;
end
xMeans = mean(dataX);
xVars = var(dataX);
for i = 1:m
xMat(i,:) = (dataX(i,:) - xMeans)./xVars;
end
% 运算30次
testNum = 30;
weights = zeros(testNum, n-1);
for i = 1:testNum
w = ridgeRegression(xMat, yMat, exp(i-10));
weights(i,:) = w';
end
% 画出随着参数lam
hold on
axis([-9 20 -1.0 2.5]);
xlabel log(lam);
ylabel weights;
for i = 1:n-1
x = -9:20;
y(1,:) = weights(:,i)';
plot(x,y);
end
岭回归求回归系数的函数
function [ w ] = ridgeRegression( x, y, lam )
xTx = x'*x;
[m,n] = size(xTx);
temp = xTx + eye(m,n)*lam;
if det(temp) == 0
disp('This matrix is singular, cannot do inverse');
end
w = temp^(-1)*x'*y;
end
逻辑回归
逻辑回归将样本特征和样本发生的概率联系起来,用于解决分类问题。
Sigmoid 函数
在最简单的二分类中,逻辑回归里样本发生的概率的值域为 [0, 1],对于线性回归
y
^
=
θ
T
⋅
x
b
\\haty = \\theta^T·x_b
y^=θT⋅xb,为了将
y
^
\\hat y
y^ 映射到值域 [0, 1] 中,引入了
σ
\\sigma
σ 函数得到了概率函数
p
^
\\hat p
p^,即:
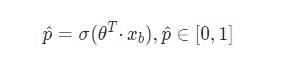
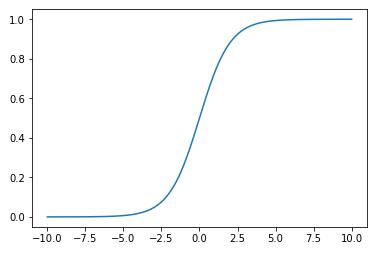
Sigmoid 函数 σ \\sigma σ 表示为: σ ( t ) = 1 1 + e − t \\sigma(t)=\\frac11+e^-t σ(t)=1+e−t1,图示如下:
当 t > 0 时, σ \\sigma σ > 0.5;当 t < 0 时, σ \\sigma σ < 0.5。因此可对二分类的分类方式为:
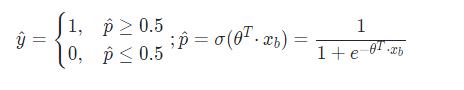
损失函数
如果实际的分类为1,p 越小时,损失越大;如果实际的分类为0,p 越大时,损失越大。引入 log 函数表示则为:
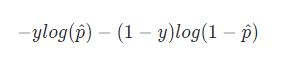
当 y=0 时,损失为 − l o g ( 1 − p ^ ) -log(1-\\hat p) −log(1−p^);当 y=1 时,损失为 − l o g ( p ^ ) -log(\\hat p) −log(p^)。
对于有 m 样本的数据集 (X, y),损失函数为:
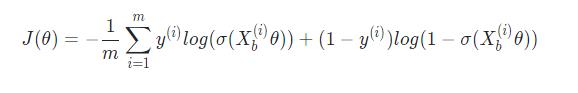
其中: X b ( i ) = ( 1 , x 1 ( i ) , x 2 ( i ) , . . . , x n ( i ) ) X_b^(i) = (1,x_1^(i),x_2^(i),...,x_n^(i)) Xb(i)=(1,x1(i),x2(i),...,xn(i)); θ = ( θ 0 , θ 1 , θ 2 , . . . , θ n ) T \\theta = (\\theta_0, \\theta_1, \\theta_2,..., \\theta_n)^T θ=(θ0,θ1,θ2,...,θn)T。
损失函数的梯度
为了得到在损失尽可能的小的情况下的
θ
\\theta
θ,可以对
J
(
θ
)
J(\\theta)
J(θ) 使用梯度下降法,结果为:
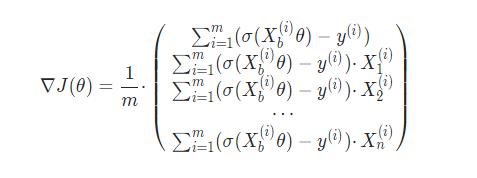
略去了公式的推导过程。
进行向量化处理后结果为:
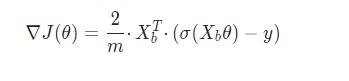

实现二分类逻辑回归算法
使用 Scikit Learn 的规范将逻辑回归的过程封装到 LogisticRegression 类中。
init() 方法首先初始化逻辑回归模型,theta 表示 θ \\theta θ,interception 表示截距,chef_ 表示回归模型中自变量的系数:
class LogisticRegression:
def __init__(self):
self.coef_ = None
self.interceiption_ = None
self._theta = None
_sigmoid() 方法实现 Sigmoid 函数:
def _sigmoid(self, t):
return 1 / (1 + np.exp(-t))
fit() 方法根据训练数据集训练模型,J() 方法计算损失 J θ J\\theta Jθ,dJ() 方法计算损失函数的梯度 ∇ J ( θ ) \\nabla J(\\theta) ∇J(θ),gradient_descent() 方法就是梯度下降的过程,X_b 表示添加了 x 0 ( i ) ≡ 1 x_0^(i)\\equiv1 x0(i)≡1 的样本特征数据:
def fit(self, X_train, y_train, eta=0.01, n_iters=1e4):
def J(theta, X_b, y):
y_hat = self._sigmoid(X_b.dot(theta))
try:
return - np.sum(y * np.log(y_hat) + (1 - y) * np.log(1- y_hat) ** 2) / len(y)
except:
return float('inf')
def dJ(theta, X_b, y):
return X_b.T.dot(self._sigmoid(X_b.dot(theta)) - y) /len(y)
def gradient_descent(X_b, y, initial_theta, eta, n_iters=n_iters, epsilon=1e-8):
theta = initial_theta
i_ters = 0
while i_ters < n_iters:
gradient = dJ(theta, X_b, y)
last_theta = theta
theta = theta - eta * gradient
if (abs(J(theta, X_b, y) - J(last_theta, X_b, y)) < epsilon):
break
i_ters += 1
return theta
X_b = np.hstack([np.ones((len(X_train), 1)), X_train])
initial_theta = np.zeros(X_b.shape[1])
self._theta = gradient_descent(X_b, y_train, initial_theta, eta)
self.interception_ = self._theta[0]
self.coef_ = self._theta[1:]
return self
predict_proba() 将传入的测试数据与训练好模型后的 θ \\theta θ 经过计算后返回该测试数据的概率:
def predict_proba(self, X_predict):
X_b = np.hstack([np.ones((len(X_predict), 1))以上是关于三天爆肝快速入门机器学习:线性回归逻辑回归岭回归第三天的主要内容,如果未能解决你的问题,请参考以下文章