室内移动机器人二维激光数据线特征提取算法的总结与开源算法分享
Posted 秃头队长
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了室内移动机器人二维激光数据线特征提取算法的总结与开源算法分享相关的知识，希望对你有一定的参考价值。
本文章总结并翻译于 A comparison of line extraction algorithms using 2D rangedata for indoor mobile robotics
除此之外，列举了其他几种方法，该文章会不断更新遇到的新算法，还有线特征相关的资料。
后续可能会涉及到激光其他的高级特征，如圆弧特征、直角特征等等，欢迎留言私信交流～
摘要：
本文介绍了应用于室内环境二维激光扫描的不同线提取算法的实验评估。选择并测试了移动机器人和计算机视觉中的六种流行算法。通过使用不同平台从两个办公环境中收集的 真实激光 数据用于实验中，以评估算法。提出并讨论了几种比较标准，以突出每种算法的优缺点，包括速度、复杂性、正确性和精度。使用标准统计方法将算法的结果与基本事实进行比较。进行了扩展的案例研究，以进一步评估 SLAM 应用程序中的算法
1 介绍
对于移动机器人来说，能够在已知或未知的环境中自主导航和定位是很重要的。精确的位姿估计始终是任何导航系统的核心，例如定位、地图构建或路径规划。众所周知，纯航位推算方法，例如里程计，容易出现随时间增长的累计误差。该问题产生了使用不同外部传感器（声纳、红外、激光、视觉等）的各种解决方案。在不同类型的传感器中，二维激光测距仪在移动机器人中越来越受欢迎，与其他传感器相比，激光扫描仪有许多优点：它们提供密集和更准确的距离测量，它们具有高采样率、高角度分辨率、良好的距离和分辨率。
一个主要问题是如何将感知数据与先验地图中的信息或已连续收集的信息准确匹配。移动机器人中使用了两种常见的匹配技术：基于点的匹配和基于特征的匹配。 Cox (1991) 的早期工作使用范围数据来帮助机器人在一个小的多边形环境中进行自我定位。他提出了一种使用迭代最小二乘最小化方法在先验图中点图像和目标模型之间的匹配算法。 Lu 和 Milios (1994) 完成的另一项工作解决了未知环境中的自我定位问题，不一定是多边形。所提出的方法是近似地对齐两个连续的扫描，然后通过定义和最小化扫描之间的一些距离来迭代地优化对齐。
基于特征的匹配不是直接使用原始测量点，而是首先将原始扫描转换为几何特征。然后在下一步中使用提取的特征进行匹配。这种方法在最近关于特征提取、特征跟踪、机器人定位、动态地图构建等得到了深入研究和应用。由于基于特征的匹配更紧凑，它们需要更少的内存，但仍能提供丰富而准确的信息。因此，与基于点的算法相比，基于参数化几何特征的算法更有效。
在众多几何图元中，线段是最简单的。使用线段很容易描述大多数办公环境。在移动机器人中，已经有许多从 2D激光数据中提取的线特征的算法。 Castellanos 和 Tardós (1996) 提出了一种受计算机视觉算法启发的线分割方法，该方法与先验地图一起用作机器人定位的方法。范多普等人(1996) 介绍了一种基于几何特征的动态地图构建算法，例如线和圆，使用激光扫描仪。 Arras 和 Siegwart (1997) 在基于地图的定位中使用基于线回归的二维扫描分割方法。 Jensfelt 和 Christensen (1998) 提出了一种通过提取正交线（墙）来使用激光扫描仪在办公环境中获取和跟踪移动机器人姿势的技术。菲斯特等人 (2003) 提出了一种使用加权线拟合的线提取算法，用于基于线特征地图构建。最后，Brunskill 和 Roy (2005) 提出了一种增量概率技术来提取片段以解决 SLAM 问题。
在线提取方面已经做了很多工作。然而，目前提出的算法缺乏全面的比较。选择从激光数据中提取线的最佳方法，是任何打算使用 2D 激光构建基于线的导航系统的人的首要任务。在速度方面，对于他的实时应用，人们会更喜欢最快的算法。在质量方面，在基于线特征的SLAM中，差的线特征提取会严重导致系统发散。实现复杂性也是需要考虑的主要方面之一。
Gutmann 和 Schlegel (1996) 所做的工作是对三种算法进行了简要比较，这些算法与最近研究中发现的算法相比相对过时。此外，他们的论文中没有介绍所用参数的不确定性建模。 Borges 和 Aldon (2004) 提出了拆分和合并的扩展版本，并将他们的方法与通用拆分和合并算法和线跟踪（增量）算法进行了比较。Sack 和 Burgard (2004) 对激光数据上的三种选定算法进行了比较。然而，在这两篇论文中，评估结果都是从映射过程构建的地图中间接观察和解释的。仍然缺少使用概率分析对提取线特征算法的直接比较。
本文对应用于激光距离扫描的六种线提取算法进行了全面评估。这项工作是（Nguyen et al.2005）中描述的工作的扩展。六种选定的算法是移动机器人和计算机视觉中最常用的算法。提出并讨论了几个比较标准，包括速度、复杂性、正确性和精度。实验是在从自主系统实验室收集的两个数据集上进行的—EPFL，瑞士和英特尔琼斯农场校园，俄勒冈州，环境尺寸分别为 80 m×50 m 和 40 m×40 m。使用标准统计方法将算法的结果与基本事实进行比较。当使用不同的线提取算法时，执行一个案例研究来评估从 SLAM 应用程序获得的地图，最后给出结论。
2 问题陈述
一个测距扫描描述了环境的二维切片。测据扫描的点在极坐标系
(
ρ
i
，
θ
i
)
(ρi，θi)
(ρi，θi)中指定，其原点是传感器的位置（或通过安装距离得到的机器人位置偏移）。通常假设距离测量中的噪声遵循具有零均值和方差
σ
ρ
i
2
σ^2_ρi
σρi2 的高斯分布。为了便于计算线参数的协方差矩阵，忽略较小的角度不确定性。值得注意的是在这项工作中，我们更关注算法的性能，而不考虑系统误差，因为它们主要取决于特定的硬件和测试环境。
我们选择极坐标形式来表示线模型：
x
c
o
s
a
+
y
s
i
n
a
=
r
xcosa + y sina = r
xcosa+ysina=r其中
−
π
<
α
≤
π
−π<α≤π
−π<α≤π是
x
x
x轴与直线法线的夹角；
r
≥
0
r≥0
r≥0是直线到原点的垂直距离；
(
x
,
y
)
(x,y)
(x,y)是直线上一点的笛卡尔坐标。
线参数的协方差矩阵为：
c
o
v
(
r
,
a
)
=
[
σ
r
2
σ
r
a
σ
r
a
σ
a
2
]
cov(r,a) = \\beginbmatrix \\sigma^2_r & \\sigma_ra \\\\ \\sigma_ra & \\sigma^2_a \\\\ \\endbmatrix
cov(r,a)=[σr2σraσraσa2]未知环境下的线提取主要存在三个问题：
- 有多少条线？
- 哪些点属于哪条线？
- 给定属于一条线的点，如何估计线模型参数?
在算法实现过程中，我们尽量多使用常用的例程，使实验结果主要反映算法概念的差异。特别是对于第三个问题，我们使用一种通用的拟合方法，称为总体最小二乘法（total-least-squares），因为它已在文献中广泛使用。因此，算法的不同之处仅在于解决前两个问题。关于参数设置，我们定义了2组参数。第一组由输入数据参数（例如每次扫描的点数）、传感器模型（例如传感器不确定性）、期望输出（例如线段的最小长度、最大不确定性）和常用例程的参数（例如聚类、合并函数）。对于所有算法，这些参数设置为相同的值。第二组由单个算法过程的特定参数值组成。这些参数是根据实验调整为每个算法单独选择的，以便在多次运行中获得最佳性能
对于最新的激光测距仪的高频率（对于 SICK LMS 200，频率高达 75 Hz），我们假设扫描是分批获得的（半个或整个扫描周期）。我们还假设机器人运动对单个扫描点（一批）的影响可以忽略不计。然而，这仅在机器人平移和旋转速度较小时成立，例如几米每秒。对于户外导航，可能需要修改这个假设。
3 选定的算法和相关工作
本节简要介绍六种选定线提取算法的概念。我们的选择是基于它们在移动机器人和计算机视觉方面的表现和受欢迎程度。尽管细节可能在不同的实现和应用中有所不同，但仅总结了算法的基本版本。有兴趣的读者应参考指定的参考资料以获取更多详细信息。如果没有另外说明，我们的实现将严格遵循下面描述的伪代码。
3.1 分割合并算法
Split-and-Merge 可能是最流行的线提取算法，它起源于 1974 年的计算机视觉，由 Pavlidis 和 Horowitz (1974) 提出，它已被广泛的研究和使用。
在实现中，我们对第 3 行进行了小修改，以便我们搜索一个分割位置，其中两个相邻点 P1 和 P2 位于该线的同一侧，并且到该线的距离都大于阈值（如果只找到 1 个这样的点，它作为噪声点被忽略）。直观地说，我们应该在离线具有局部最大距离的点处分割。请注意，在第 2 行中，我们使用最小二乘进行线拟合。
可以以不同的方式实现该算法，以便通过连接第一个点和最后一个点来简单地构造一条线。在这种情况下，该算法也被称为迭代终点法。
3.2 增量算法
简单是该算法的主要优点。它已在许多应用中使用，也被称为线跟踪。
在实现中，我们每一步骤（第2行）添加5个测量点以加快增量过程。当线特征不满足预定义的线特征条件时（线特征的差异小于某个阈值），将5个点放回来，算法将返回正常模式（一次添加一个测量点）。再次，我们使用总体最小二乘算法进行拟合。
增量方案已在算法中使用，然而，他们使用EKF来估计相当线的参数，这相当于在本文中使用完全的最小二乘。
3.3 霍夫变换算法
Hough 变换最成功地应用于强度图像中的线查找（Forsyth 和 Ponce2003）。它已被引入机器人技术，用于从扫描图像中提取线条。
霍夫变换有一些缺点：
- 通常难以为累加器数组选择合适的网格大小。
- 基本霍夫变换算法在估计线参数时不考虑噪声和不确定性
在这个实现中，我们分别使用 1 c m 1 cm 1cm和 0.4 ° 0.4° 0.4°的分辨率作为范围和角度的网格大小。为了克服第二个问题，我们使用总体最小二乘法进行线拟合（第 7 行）。为了提高线提取的性能，已经提出了几种霍夫变换的变体，例如随机霍夫变换，范围加权霍夫变换，对数霍夫变换。
3.4 线回归算法
该算法已 (Arras 和 Siegwart1997) 提出用于基于地图的定位。其关键思想来源于霍夫变换算法，该算法首先将线提取问题转化为模型空间（线参数域）中的搜索问题，然后应用凝聚层次聚类（AHC）算法构造相邻线段。该算法的一个缺点是实现起来相当复杂。
最佳滑动窗口大小 N f N_f Nf 取决于环境，对算法性能有很大影响。对于我们的基准，使用 N f N_f Nf =7。第 2 行使用了总体最小二乘拟合方法。
3.5 RANSAC算法
RANSAC-Random Sample Consensus（Fischler 和 Bolles1981）是一种用于在存在数据异常值的情况下对模型进行稳健拟合的算法。 RANSAC 的主要优点是它是一种通用的分割方法，一旦我们有了特征模型，它就可以与多种类型的特征一起使用。实现起来也很简单。该算法在计算机视觉中非常流行以提取特征（Forsyth and Ponce2003）。同样，第 4、7 行使用了相同的拟合方法。
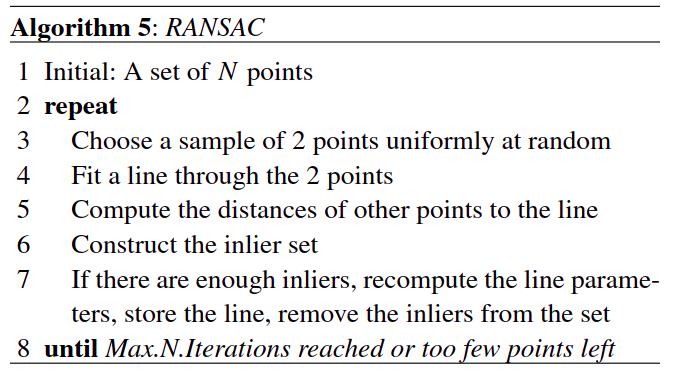
3.6 EM 算法
期望最大化（EM）是一种概率方法，常用于缺失变量问题。EM已被用作计算机视觉（Forsyth和Ponce2003）和机器人（Liu et al.2001; Pfister et al. .2003；Sack 和 Burgard 2004)。
EM 算法有一些缺点：
- 它可能会陷入局部最小值
- 难以选择好的初始值
3.7 额外细节
如前所述，一旦我们有一组由算法确定的内点，我们就使用相同的总体最小二乘法来计算线的线参数及其协方差矩阵。这种技术克服了众所周知的最小二乘法的偏差问题，它倾向于将更多的权重放在嘈杂的离群点上（Forsyth 和 Ponce2003）。有关总体最小二乘法的详细信息，请参阅 Arras and Siegwart 1997
我们实现了一个简单的聚类算法，用于滤除大量噪声测量点，并将原始扫描粗略地划分为扫描点的子组（集群）。该算法的工作原理类似于SEF（连续边缘跟随）算法。简而言之，它按顺序扫描来自传感器的原始扫描点，以查找连续点之间径向差异的大跳跃。如果径向差大于阈值，则该算法将此时的扫描序列分成两个子组。因此，扫描被分割成连续点的簇。删除点数太少的集群。为了安全和避免过度分割，我们使用非常保守的阈值值。当一条线段在中间包含一个噪声点（例如由于噪声或遮挡）时，可以通过考虑过度分割的情况来改进这种聚类算法。在这种情况下，两个分割段可以在之后合并（在下一段中描述）。然而风险在于，如果一个或两个子段太小，它们可能在到达合并步骤之前被移除。幸运的是，这个问题在我们的实验中很少出现。
由于遮挡，可能会观察到一条线并将其提取为几个段。定位算法通常在位置估计中使用线参数
(
r
,
α
)
(r, α)
(r,α)。因此，将共线的线段合并为一个线段可能是一个好主意。它会产生更长的线段，因此更可靠，减少了要处理的线数并且仍然包含相同的线段信息。因此，我们实现了一个合并例程，该例程在提取线段之后应用于每个算法的输出。该例程使用称为卡方检验的标准统计方法，根据已经计算的线参数协方差矩阵计算每对线段之间的马氏距离。如果两条线段的统计距离小于阈值，则将它们合并。新的线参数从构成两条线段的原始扫描点并重新计算。
4 实验结论
为了分析实验结果，评估了四个量测：复杂性、速度、正确性和精确性。基准测试结果如表 1 和表 2 所示。共有 11 个候选算法，其中 6 个是与我们的简单聚类算法相结合的选定算法（显示为“+聚类”）。其他 5 个候选是相应算法的基本版本。表中使用的术语如下（括号中使用的值）：
- N N N：输入扫描中的点数（722 或 181）
- S S S：算法提取的线段数
- N f N_f Nf：线回归 的滑动窗口大小
- N . T r i a l s N.Trials N.Trials：RANSAC(1000) 的试验次数
- N R , N C NR,NC NR,NC：HT累加数组的行数和列数（ N R = 671 NR=671 NR=671， N C = 901 NC=901 NC=901，分辨率 r r e s = 1 c m r_res=1cm rres=1cm， α r e s = 0.4 ◦ α_res=0.4◦ αres=0.4◦ )
- N 1 , N 2 N1,N2 N1,N2：试验次数和收敛迭代次数，分别为 E M ( N 1 = 50 , N 2 = 200 ) EM(N1=50,N2=200) EM(N1=50,N2=200)。
常用例程，例如聚类、总体最小二乘法拟合和线合并，复杂度都是
N
N
N。
正确性度量定义如下：
T
r
u
e
P
o
s
=
N
.
M
a
t
c
h
e
s
N
.
T
r
u
e
L
i
n
e
s
TruePos=N.Matches \\over N.TrueLines
TruePos=N.TrueLinesN.Matches
F
a
l
s
e
P
o
s
=
N
.
L
i
n
e
E
x
B
y
A
l
g
o
−
N
.
M
a
t
c
h
e
s
N
.
L
i
n
e
E
x
B
y
A
l
g
o
FalsePos=N.LineExByAlgo−N.Matches \\over N.LineExByAlgo
FalsePos=N.LineExByAlgoN.LineExByAlgo−N.Matches其中
N
.
L
i
n
e
E
x
B
y
A
l
g
o
N.LineExByAlgo
N.LineExByAlgo是提取的线数一种算法，
N
.
M
a
t
c
h
N.Match
N.Match 是匹配的数量，
N
.
T
r
u
e
L
i
n
e
N.TrueLine
N.TrueLine是真实行的数量。
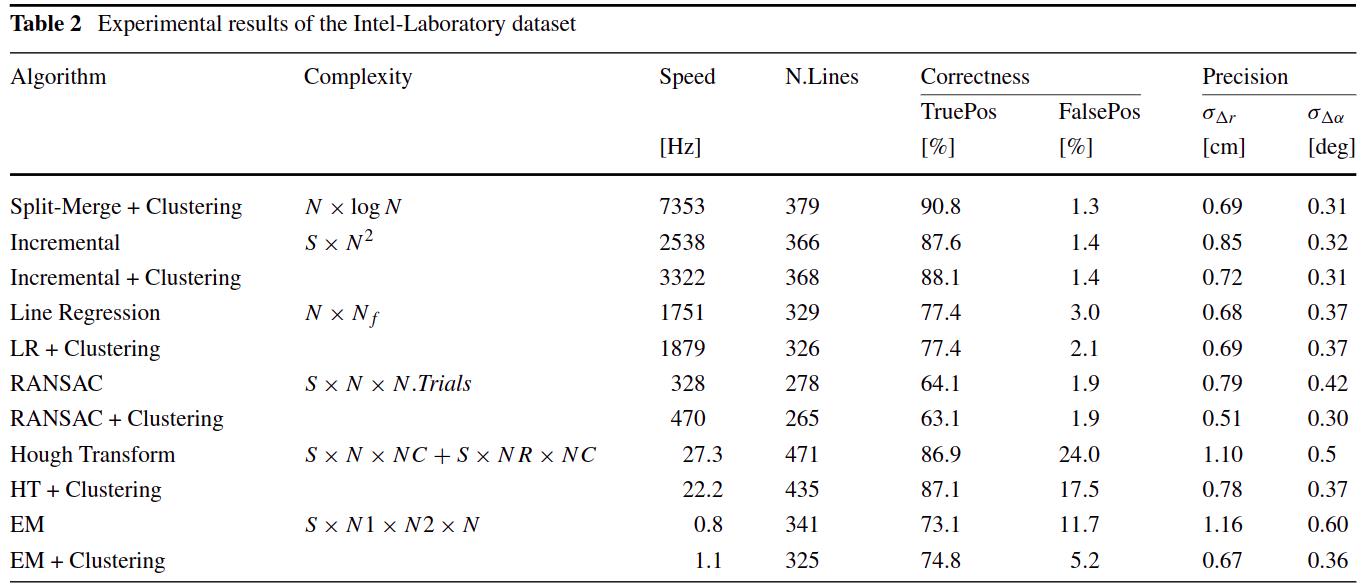
总体而言，实验结果表明，
S
p
l
i
t
−
a
n
d
−
M
e
r
g
e
Split-and-Merge
Split−and−Merge和
I
n
c
r
e
m
e
n
t
a
l
Incremental
Incremental这两种算法具有最佳的性能，因为它们具有优越的速度和正确性.对于实时应用，
S
p
l
i
t
−
a
n
d
−
M
e
r
g
e
Split-and-Merge
Split−and−以上是关于室内移动机器人二维激光数据线特征提取算法的总结与开源算法分享的主要内容，如果未能解决你的问题，请参考以下文章