2022年蓝桥杯第二次校内选拔赛
Posted 容艾假
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了2022年蓝桥杯第二次校内选拔赛相关的知识,希望对你有一定的参考价值。
河南农业大学校内赛
榜单
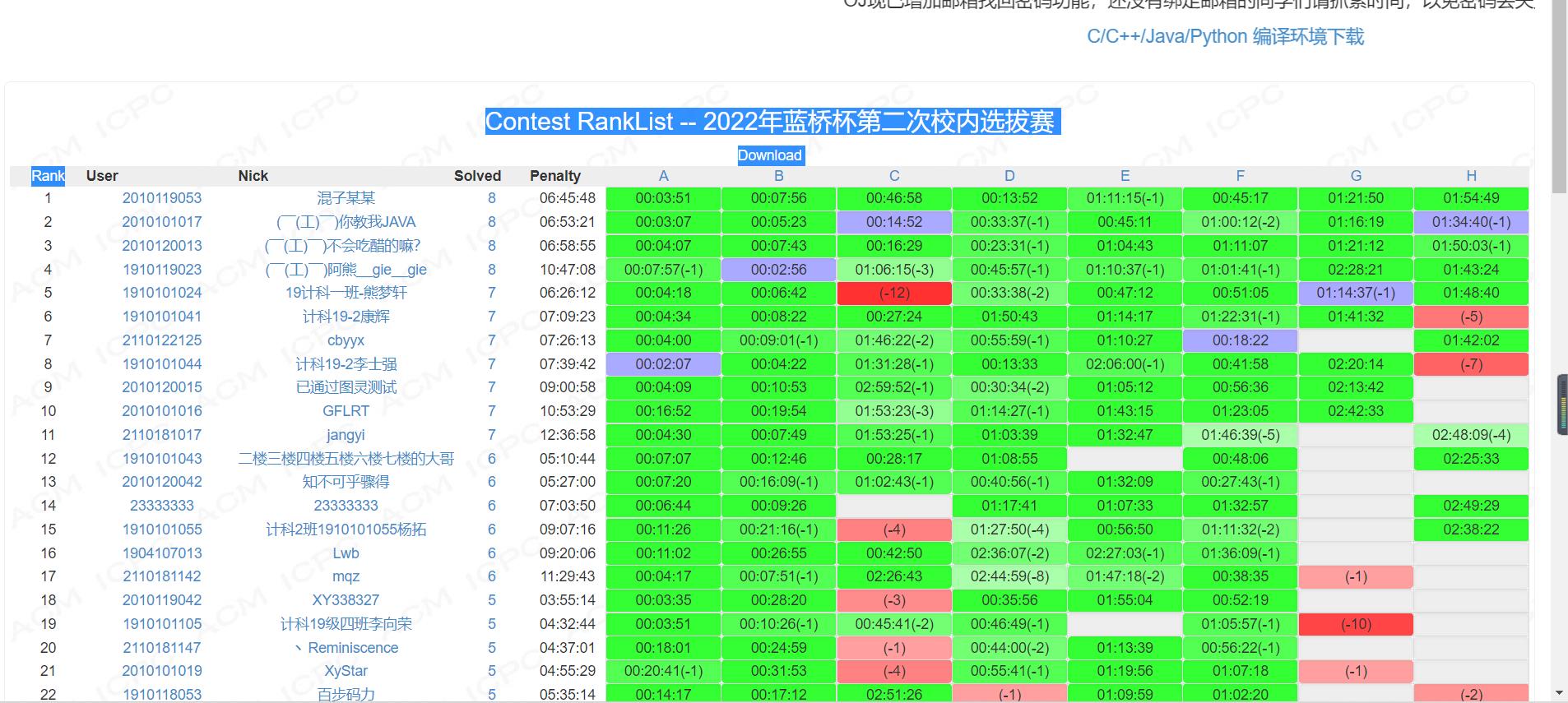
正文
问题 A: 单调数列
题目描述
题目描述
如果数组是单调递增或单调递减的,那么它是单调的。如果对于所有 i <= j,nums[i] <= nums[j],那么数组 nums 是单调递增的。 如果对于所有 i <= j,nums[i]> = nums[j],那么数组 nums 是单调递减的。当给定的数组 nums 是单调数组时输出"YES",否则输出"NO"。
输入
第一行输入一个正整数n表示数组大小(1<=n<=100000)
第二行输入n个[1,100000000]整数
输出
当给定的数组 nums 是单调数组时输出"YES",否则输出"NO"。
样例输入
4
4 3 2 1
样例输出
YES
题目思路及代码
签到题目
#include<bits/stdc++.h>
using namespace std;
typedef long long int ll;
const ll maxn = 1e5+10;
ll a[maxn];
ll n;
int main()
cin>>n;
for(int i=1;i<=n;i++)
cin>>a[i];
ll flag=0;
for(int i=2;i<n;i++)
ll f=(a[i]-a[i-1]);
ll f1=a[i+1]-a[i];
if(f<0&&f1>0)
flag=1;
break;
else if(f>0&&f1<0)
flag=1;
break;
if(flag)
cout<<"NO";
else
cout<<"YES";
return 0;
问题 B: 最大连续1的个数
题目描述
题目描述
给定一个正整数n,请你计算n在二进制表示下最大连续1的个数。例如:正整数55的二进制表示为110111,则答案为3。
输入
输入一个正整数n(1<=n<=1e9)
输出
输出n在二进制表示下最大连续1的个数
样例输入
55
样例输出
3
题目思路及代码
先转化为二进制,用一个简单队列获取结果
#include<bits/stdc++.h>
using namespace std;
typedef long long int ll;
const ll maxn = 1e5+10;
ll a[maxn];
ll n;
ll cnt=0;
int main()
cin>>n;
while(n)
a[++cnt]=n%2;
n/=2;
ll l=0,r=0;
ll ma=0;
for(int i=1;i<=cnt;i++)
//cout<<a[i]<<" ";
if(a[i]==1)
r++;
else
l=i;
r=l;
ma=max(r-l,ma);
cout<<ma;
return 0;
问题 C: 祖玛游戏
题目描述
题目描述
给你一个只含有小写字母的字符串s,请你从左至右在 s 中选择第一个 k 个相邻且相等的字母,并删除它们,使被删去的字符串的左侧和右侧连在一起。你需要对 s 重复进行无限次这样的删除操作,直到无法继续为止。在执行完所有删除操作后,输出最终得到的字符串。
输入
整数k和字符串s,(2<=k<=5,1<=|s|<=1000000)
输出
输出执行完所有删除操作后最终得到的字符串。
样例输入
3
deeedbbcccbdaa
样例输出
aa
题目思路及代码
直接用暴力进行删除,知道不能在进行删除位置
#include<bits/stdc++.h>
using namespace std;
typedef long long int ll;
const ll maxn = 1e6+10;
ll k;
ll n;
char str[maxn],str1[maxn];
int find1(ll x)
ll s=1;
//cout<<x+k<<endl;
for(int i=x+1;i<(x+k);i++)
if(i>n)break;
if(str[i]==str[x]&&(i-x)<k)
//cout<<i<<" ";
s++;
//cout<<s<<endl;
if(s==k)
return 1;
else
return 0;
int main()
cin>>k;
cin>>(str+1);
n=strlen(str+1);
ll cnt=0;
//ll k=0;
while(1)
//k++;
ll flag=0;
for(int i=1;i<=n;i++)
//cout<<i<<endl;
//cout<<find1(i)<<endl;
if(find1(i))
//cout<<i<<" ";
i=i+k-1;
flag=1;
//cout<<i<<endl;
else
str1[++cnt]=str[i];
/*for(int i=1;i<=cnt;i++)
cout<<str1[i];
cout<<cnt<<endl;*/
if(!flag)
break;
for(int i=1;i<=cnt;i++)
str[i]=str1[i];
n=cnt;
cnt=0;
for(int i=1;i<=cnt;i++)
cout<<str1[i];
return 0;
/*
2
deeedbbcccbdaa
*/
问题 D: 因数
题目描述
题目描述
给定正整数n,n只能被素因子2、3、5整除,请你求出正整数n能被2整除的因数个数。例如:n=6,6的因数为:1、2、3、6。答案为2。
输入
正整数n(1<=n<=1e16)
输出
求出正整数n能被2整除的因数个数
样例输入
6
样例输出
2
题目思路及代码
通过暴力获取结果,也可以通过唯一分解定理来求解,结果为a*(b+1)*(c+1)
#include<bits/stdc++.h>
using namespace std;
typedef long long int ll;
const ll maxn = 1e5+10;
ll n;
ll cnt=0;
int main()
cin>>n;
// n=1e16;
for(ll i=1;i*i<=n;i++)
if(n%i==0)
if(i*i!=n)
ll t=n/i;
if(t%2==0)cnt++;
if(i%2==0)cnt++;
else
if(i%2==0)cnt++;
cout<<cnt;
return 0;
E: 计算24
题目描述
题目描述
游戏规则是:对4个 1∼10 之间的正整数,进行加、减、乘三种运算,要求运算结果等于二十四。乘法的优先级高于加、减,并且算式中不可以用括号,不可以改变4个数字出现的顺序。例如:若给出的 44个操作数是:10、2、4、8,则有2种可能的解答方案:10+2+4+8=24,10*2-4+8=24。现在给你4个1∼10 之间的正整数,请你计算解答方案数。
输入
4个 1∼10 之间的正整数
输出
输出方案总数
样例输入
10 2 4 8
样例输出
2
题目思路及代码
直接暴力枚举27种情况
#include<bits/stdc++.h>
#include<string.h>
using namespace std;
long long n,m,k;
int num,numm;
long long maxx[100010],minn[100010];
int flag;
int j=0;
int cont;
int a,b,c,d;
int main()
cin>>a>>b>>c>>d;
if(a+b+c+d==24||a+b+c*d==24||a+b+c-d==24||a+b*c+d==24||a+b*c*d==24||a+b*c-d==24||a+b-c+d==24||a+b-c*d==24||a+b-c-d==24)cont++;
if(a*b+c+d==24||a*b+c*d==24||a*b+c-d==24||a*b*c+d==24||a*b*c*d==24||a*b*c-d==24||a*b-c+d==24||a*b-c*d==24||a*b-c-d==24)cont++;
if(a-b+c+d==24||a-b+c*d==24||a-b+c-d==24||a-b*c+d==24||a-b*c*d==24||a-b*c-d==24||a-b-c+d==24||a-b-c*d==24||a-b-c-d==24)cont++;
cout<<cont;
return 0;
问题 F: 子集和
题目描述
题目描述
给你一个元素个数不超过30的整数集合,请你计算该集合所有子集的元素之和。例如集合1,4,则该集合的子集共四个空集、1、4、1、4,则子集的元素之和为1+4+1+4=10。
输入
第一行一个正整数n(1<=n<=30)
第二行n个大小在[1,1000000]范围内的正整数
输出
输出给定集合所有子集的元素之和
样例输入
2
1 4
样例输出
10
题目思路及代码
直接用结论元素之和乘以2的n-1次方
#include<bits/stdc++.h>
using namespace std;
typedef long long int ll;
const ll maxn = 1e5+10;
ll n;
ll a[maxn];
ll sum=0;
int main()
//cin>>n;
//n=30;
scanf("%lld",&n);
for(int i=1;i<=n;i++)
//cin>>a[i];
//a[i]=1;
scanf("%lld",&a[i]);
sum+=a[i];
/* ll sum=pow(2,n)-1;
//cout<<sum;
ll cnt=0;
for(ll i=1;i<=sum;i++)
//cout<<i<<endl;
ll k=i;
for(ll j=n;j>=1;j--)
ll t=k&1;
k>>=1;
//k++;
if(t==1)
cnt+=a[j];
*/
sum=sum*pow(2,n-1);
printf("%lld\\n",sum);
return 0;
/*
*/
G: 最大整除
题目描述
题目描述
给你一个正整数k和一个整数数组 a,请你求出能被k整除的元素最大和。
输入
第一行两个正整数n和k,分别表示数组大小和题目中的k。(1<=n<=40000,2<=k<=20)
第二行n个[1,1000000]范围内的整数
输出
输出能被k整除的元素最大和。
样例输入
5 3
3 6 5 1 8
样例输出
18
提示
样例中选择3、6、1、8,3+6+1+8=18
题目思路及代码
动态规划,其实是背包变形,刚开始的代码为:
dp[0]=1;
for(ll i=1;i<=n;i++)
//dp[i]=1;
for(ll j=sum;j>=a[i];j--)
if(dp[j-a[i]])
dp[j]=1;
但是经过计算后发现超时,因此需要进行取模来进行优化
#include<bits/stdc++.h>
using namespace std;
typedef long long int ll;
const ll maxn = 1e5+10;
ll n,k;
ll a[maxn],dp[maxn][100];
ll sum=0;
int main()
cin>>n>>k;
for(int i=1;i<=n;i++)
cin>>a[i];
//dp[i]=1;
//sum+=a[i];
//sort(a+1,a+1+n);
memset(dp,-0x3f,sizeof(dp));
dp[0][0]=0;
for(ll i=1;i<=n;i++)
for(ll j=0;j<k;j++)
dp[i][j]=max(dp[i-1][j],dp[i-1][(j-a[i]%k+k)%k]+a[i]);
cout<<dp[n][0];
return 0;
H: 种树
题目描述
题目描述
A市为了响应国家碳达峰碳中和目标要求,欲购买一批树苗来净化A市的空气。现有n个树苗厂家,每个厂家有一个初始树苗单价(单位元),每购买一颗树苗后,树苗单价都会上涨1元。现需要购买m颗树苗,问最少需要多少元。
输入
第一行两个正整数n和m(1<=n<=100000,1<=m<=1e10)
第二行n个[1,10]范围内的整数表示树苗厂家初始树苗单价。
输出
购买m颗树苗的最小花费
样例输入
3 6
1 2 3
样例输出
14
题目思路及代码
从小往大进行买树,不断计算是否买够,具体看代码
#include<bits/stdc++.h>
using namespace std;
typedef long long int ll;
typedef pair<ll,ll> P;
const ll maxn = 1e7+10;
ll n,m;
ll a[maxn];
ll getmoney(ll x,ll y)
return (x+y)*(y-x+1)/2;
priority_queue<P,vector<P>,greater<P> >que;
map<ll,ll> mp,vis;
int main()
cin>>n>>m;
for(int i=1;i<=n;i++)
cin>>a[i];
mp[a[i]]++;
for(int i=1;i<=n;i++)
if(!vis[a[i]])