2021年软件类第十二届蓝桥杯第二场省赛 python组 A-E题解

Posted 2022-03-26 风信子的猫Redamancy

2021年软件类第十二届蓝桥杯第二场省赛 python组 A-E题解

文章目录

• 2021年软件类第十二届蓝桥杯第二场省赛 python组 A-E题解
• • 试题 A：求余
  • • 思路
    • 代码
    • 答案
  • 试题 B：双阶乘
  • • 思路
    • 代码
    • 答案
  • 题目 C：格点
  • • 思路
    • 代码
    • 答案
  • 试题 D：整数分解
  • • 思路
    • 代码
    • 答案
  • 试题 E：城邦
  • • 思路
    • 代码
    • 答案

试题 A：求余

思路

这道题，emmmm，没思路，直接算，可能测试一下吧

代码

print(2021%20)

答案

1

试题 B：双阶乘

思路

这道题也很简单，我们求最后五位，就是%100000，然后双阶乘，实际上就是每隔1个相乘，所以我们直接循环计算即可

代码

dp = [1]*2022

for i in range(3,2022,2):
    dp[i] = dp[i-2]*i
print(dp[2021]%100000) # 答案59375

答案

59375

题目 C：格点

思路

这道题我们的思路是很清晰的，首先我们的坐标一定是整数，这样我们的数就是格点，其次我们在第一象限获取符合条件的数

在我们的条件中，题目说，要坐标x和坐标y相乘小于等于2021，我们就可以遍历这之间的数，如果我们的数的坐标相乘小于等于2021，那我们的计数就+1，最后打印出我们最后的值即可

代码

ans = 0
for x in range(1,2021+1): # 保证起码是1~2021的数据
    for y in range(1,2021//x + 1): # 范围是1 ~ 2021//x
        if x*y <= 2021: # 如果x*y<=2021
            ans += 1
print(ans) # 答案：15698

答案

15698

试题 D：整数分解

思路

首先最简单的思路就是5重循环，不过O(n^5)的复杂度，让人望而却步，我也尝试进行一个改进一下范围，但是结果还是不近如意，除非在考试的时候，顶多运行5个小时一定出的来，或者利用C++运行应该会快很多的

好咯，废话不多说，这里讲一下正解，其实呢，这道题可以用隔板的思想

比如说3分为两个数，实际上就是3个小球，一个隔板，有几种放法，3 = 1 + 2,@|@@或者是3 = 2 + 1，@@|@，所以这就是一个组合的问题了，我们可以看到，3个小球有2个空隙（最前面和最后面不算），放一个隔板，就是$C_2^1$

所以这样来看，我们的2021分为五个数，就是2021个球放4个隔板，有几种放法，根据上面来看，一共2020个空隙，4个隔板，一共就是$C_{2020}^4$

代码

# cnt = 0
# for a in range(1,2022):
#     for b in range(1,2022-a-3):
#         for c in range(1,2022-a-b-2):
#             for d in range(1,2022-a-b-c-1):
#                 for e in range(1,2022-a-b-c-d):
#                     if a + b + c + d + e == 2021:
#                         cnt += 1
# print(cnt)

import math # 利用math库的组合数
print(math.comb(2020,4)) # 答案：694422703815
print(2020*2019*2018*2017*2016//5//4//3//2//1)

答案

694422703815

试题 E：城邦

思路

这道题实际上也很简单，其实就是一道最小生成数的模板题，那我们可以直接套最小生成树的模板

理清思路了以后，我们可以理清楚一下这道题的思路，首先，我们有2021个城邦，我们要使所有城邦可以互通，最大是$C_{2021}^2$种方案，相当于每两个城邦建一座桥，不过这种耗费是很大的，并且，我们的题目说了，我们会建立2020座桥，并且要求花费是最小的，所以这就是在考最小生成树的知识点

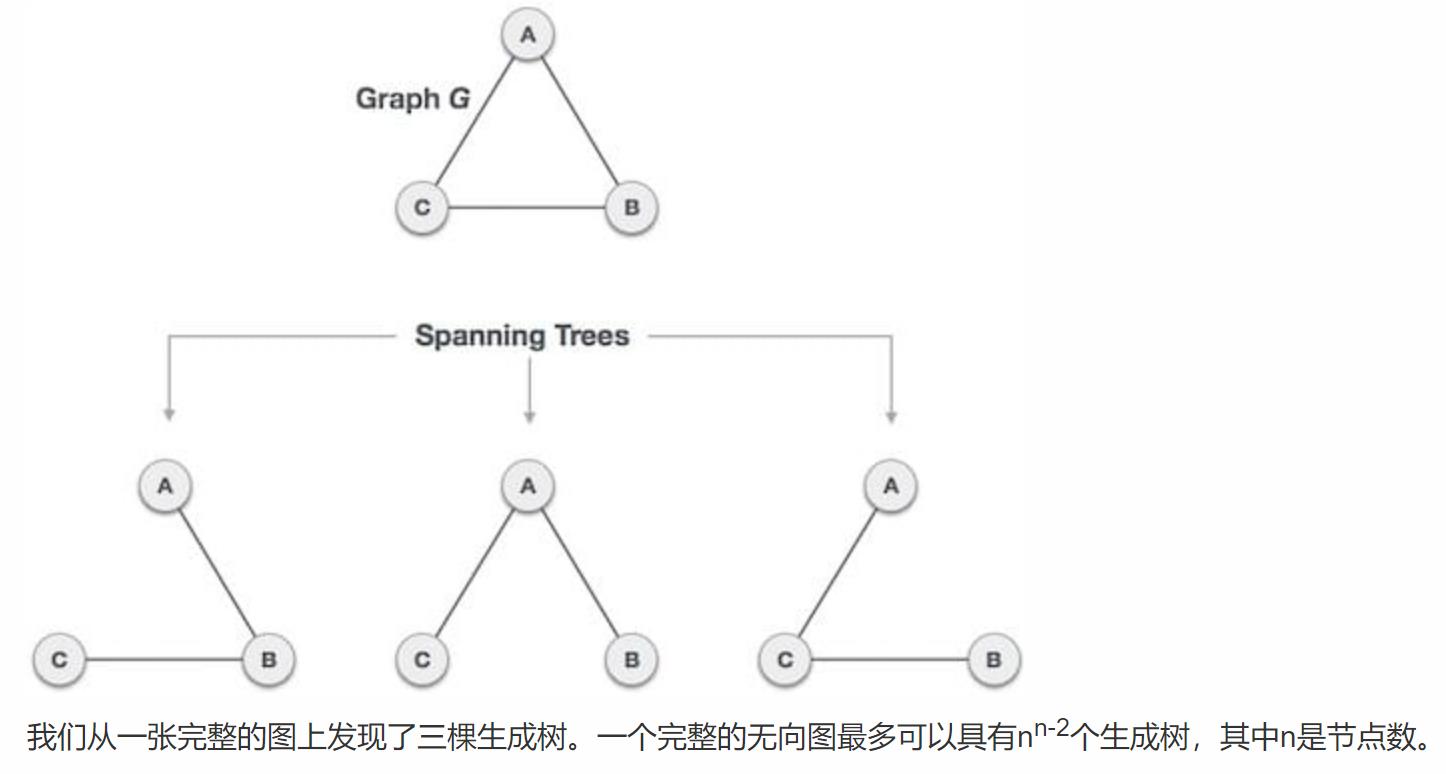
生成树定义：对于有n个顶点的连通图，只有n-1条边的连通子图就是它的生成树。（既然是树就不可能存在环）

所以简言之，生成树就是以最少的边（n-1）条边来连接所有顶点的图。但是：

生成树不唯一（取的边的组合不唯一），当我们赋予了边的权值时，所有边的权值的和也就必然有一个最小值。即最小生成树

知道定义了以后，我们这里用的是克鲁斯卡算法，kruskal的基本算法思想，创建边的数组（i,j,weihgt），按照边的权值排序（贪心），然后，初始化各个顶点作为一个独立的集合（并查集思想），遍历边（贪心）,如果i和j不在同一集合，意味着i,j不连通（并查集），对应的边应当取过来，权值和累加一次，否则如果i和j在同一集合（已经连通），意味着这条边不应取过来…直至取完n-1条边,只剩下一个集合，这个集合包含所有点（连通性）那么最终的权值和一定是最小的（最小权值和）。

代码

# 初始化祖先
father = [i for i in range(2022)]

def get_father(x):
    # 压缩路径，查找集合
    if x != father[x]:
        father[x] = get_father(father[x])
    return father[x]

# 合并两节点        
def union(x,y):
    xfather,yfather = get_father(x),get_father(y)
    if xfather != yfather:
        father[xfather] = yfather

# 计算权重
def get_weight(x,y):
    s = 0
    while x or y:
        if x%10 != y%10:
            s += x%10 + y%10
        x //= 10
        y //= 10
    return s

#创建边集(i,j,weight)
edge=[]
for i in range(1,2022):
    for j in range(1,2022):
        edge.append((i,j,get_weight(i,j)))
edge.sort(key=lambda x:x[2]) # 根据权重排序

cnt = 0
ans = 0
for i in edge:
    # 不在同一个连通分量中，并且没有建立2020座桥
    if get_father(i[0]) != get_father(i[1]) and cnt < 2020:
        union(i[0],i[1])
        cnt += 1
        ans += i[2]
print(ans) # 答案：4046

答案

4046