时间序列预测之移动平均法（MA）

Posted 2022-02-10 Icy Hunter

移动平均法
一般的移动平均法主要用于平稳序列，其主要思想就是通过对近期几个（例如五个）的数据求平均作为下一个即这五个之后的那个数据的预测值。

二次移动平均法的话就是在一次平均移动法的基础上对一次平均移动计算出来的值再进行一次移动平均。
思路还是十分简单明了的，只是公式看起来就有点乱七八糟了。

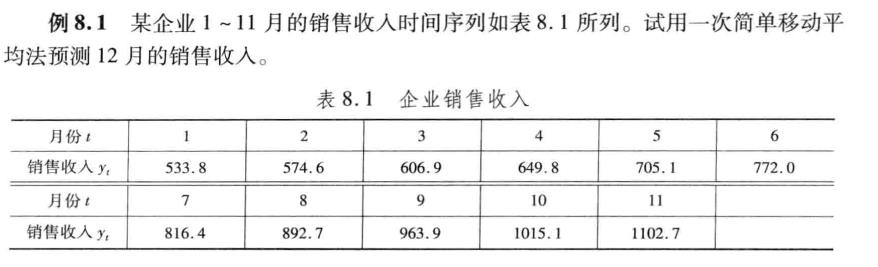
下面展示一道例题：

clc,clear
y = [533.8 574.6 606.9 649.8 705.1 772.0 816.4 892.7 963.9 1015.1 1102.7];
m = length(y);
n = [4, 5]  % n为移动平均的项数，4就是4个求平均预测
for i = 1:length(n) % 由于n的取值不同，因此使用细胞数组
    for j = 1:m - n(i) + 1
        yhati(j) = sum(y(j: j+n(i)-1))/n(i); % 从头到尾都自回归预测了一遍，最后一个才是我们需要的数
    end
    y12 = yhati(end); % 取出需要12月的预测值
    s(i) = sqrt(mean((y(n(i) + 1 : end) - yhati(1:end - 1)).^2)); % 计算误差
end
y12 = yhat1(end)
y12 = yhat2(end)
s

分析：

本文参考的是司守奎，孙兆亮主编的数学建模算法与应用（第二版）