鲁棒性检查(下)

Posted 2023-02-23 KuoGavin

文章目录

• • 10.9 统计静态时序分析(Statistical Static Timing Analysis)
  • • 10.9.1 工艺和互连走线变化(Process and Interconnect Variations)
    • 10.9.2 统计分析(Statistics Analysis)
  • 10.10 时序违例路径(Paths Failing Timing)
  • • 路径找不到(No Path Found)
    • 跨时钟域(Clock Crossing Domain)
    • 反相衍生时钟(Inverted Generated Clocks)
    • 缺少虚拟时钟延迟(Missing Virtual Clock Latency)
    • IO延迟大(Large IO Delay)
    • IO缓冲器延迟不正确(Incorrect IO Buffer Delay)
    • 延迟值不正确(Incorrect Latency Numbers)
    • 半周期路径(Half-cycle Path)
    • 较大的延迟和过渡时间(Large Delays and Transition Times)
    • 缺少多周期保持时间约束(Missing Multicycle Hold)
    • 未优化的路径(Path Not Optimized)
    • 仍不满足时序的路径(Path Still Not Meeting Timing)
    • 如果仍然不满足时序怎么办(What if Timing Still Cannot be Met)
  • 10.11 验证时序约束
  • • 检查路径例外(Checking Path Exception)
    • 检查跨时钟域(Checking Clock Domain Crossing)
    • 验证IO和时钟约束(Validating IO and Clock Constraints)
  • 知乎圣经链接

---

---

10.9 统计静态时序分析(Statistical Static Timing Analysis)

到目前为止介绍的静态时序分析技术是确定性的，因为分析基于的是设计中所有时序弧的固定延迟。每个时序弧的延迟都是根据工作条件以及工艺和互连模型计算得出的，尽管可能存在多个模式和多个角，但给定情况下的时序路径延迟是可以明确获得的。

实际上，执行$STA$时通常使用的工艺和工作条件的最差情况（$WCS$）或最佳情况（$BCF$）对应于极端的$3\sigma$角(The $\sigma$ here refers to standard deviation of an independent variable modeled statistically)。时序库基于的是代工厂提供的带有工作条件的工艺角模型，这些条件对应于单元时序值的不同角。例如，使用快速工艺模型、最高电源和最低温度来表征最佳情况的快速时序库。

科普文：半导体中名词“wafer”“chip”“die”的联系和区别是什么？

---

10.9.1 工艺和互连走线变化(Process and Interconnect Variations)

全局工艺变化(Global Process Variations)

全局工艺变化（global process variation），也称为芯片间器件变化（inter-die device variations），是指影响芯片（或晶圆）上所有器件的工艺参数变化，参见图10-24。这表明芯片上的所有器件都会受到这些工艺变化的影响，芯片上的每个器件都会是$slow$或是$fast$的，或者介于两者之间。 因此，通过全局工艺参数建模的变化旨在捕获芯片与芯片之间的变化。

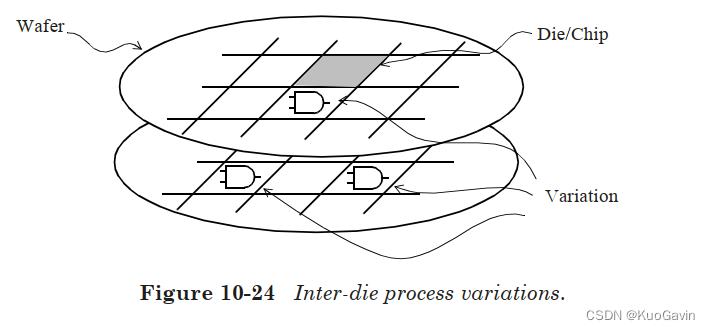
图10-25中显示了全局参数值（例如$g\_par1$）的变化。例如，参数$g\_par1$可以对应于标准（The standard device here means a device with fixed length and width.）$NMOS$器件的$IDSsat$（器件饱和电流）。由于这是一个全局参数，因此芯片上所有单元实例中的所有$NMOS$器件将对应于相同的$g\_par1$值。可以有如下选择：所有单元实例的$g\_par1$的变化是完全相关的，或者芯片上$g\_par1$的变化相互影响。注意，可能还存在其它全局参数（$g\_par2$，…），其可能可以对$PMOS$器件饱和电流和其它相关变量建模。

不同的全局参数（$g\_par1$，$g\_par2$，…）之间是不相关的。不同全局参数的变化是不会相互影响的，这意味着$g\_par1$和$g\_par2$参数彼此将独立地变化。在一块芯片上，$g\_par1$可能处于最大值，而$g\_par2$可能处于最小值。

在确定性（即非统计性）分析中，慢速工艺模型可能对应于芯片间变化的$+3\sigma$角的条件。类似地，快速工艺模型可能对应于芯片间变化的$-3\sigma$角的条件。

局部工艺变化(Local Process Variations)

局部工艺变化（local process variation），也称为芯片内器件变化，是指工艺参数的变化，这些变化可以在给定芯片上影响不同器件，参见图10-26。这意味着并排放置在同一芯片上的相同器件可能具有不同的行为。由局部工艺变化建模的变化旨在捕获芯片内的随机工艺变化。

图10-27显示了局部工艺参数的变化。芯片上的局部参数变化不会相互影响，并且它们从一个单元实例到另一单元实例的变化是不相关的。这意味着对于同一芯片上的不同器件，局部参数可能具有不同的值。例如，芯片上的不同$NAND2$单元实例可能会具有不同的局部工艺参数值。即使其它参数（例如输入压摆和输出负载）相同，这也可能导致同一$NAND2$单元的不同实例具有不同的延迟值。

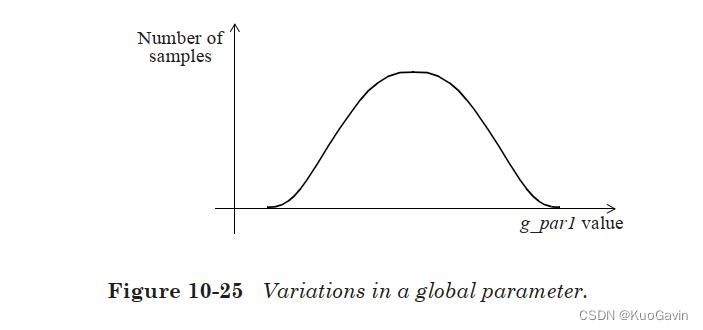
由全局和局部变化引起的NAND2单元延迟变化的示意图如图10-28所示。该图说明了全局参数变化比局部参数变化引起的延迟变化更大。

局部工艺变化是打算在使用$OCV$建模的分析中捕获的变化之一，如10.1节中所述。由于统计时序模型通常包括局部工艺变化，因此使用统计时序模型进行的$OCV$分析不应在$OCV$设置中包括局部工艺变化。

互连走线变化(Interconnect Variations)

如10.8节中所述，实际上存在着各种互连角，它们代表影响互连电阻和电容值的每个金属层的参数变化。这些参数变化通常是金属和电介质的厚度以及影响各种金属层中金属走线的宽度和间距的金属刻蚀。通常，影响金属的参数会影响该金属层中所有走线的寄生参数，但对其它金属层中走线的寄生影响很小甚至是没有影响。

10.8节中介绍的互连角可用于对互连走线变化进行建模，以便所有金属层都对应到相同的互连角下。对互连走线变化进行统计建模时，每个金属层都可以独立地变化。统计方法会对互连走线空间中所有可能的变化组合进行建模，从而对仅通过在指定互连角下进行分析可能无法捕获的变化进行建模。例如，时钟树的发起路径可能在$METAL2$中，而时钟树的捕获路径可能在$METAL3$中。传统互连角下的时序分析会考虑各种角，这些角会同时改变所有金属层，因此无法对这种情况进行建模：$METAL2$在该角下延迟最大，而$METAL3$在该角下延迟最小。这种组合对应于路径建立时间检查的最差情况，并且只能通过对互连走线变化进行统计建模来捕获。

---

10.9.2 统计分析(Statistics Analysis)

如果对单元时序模型和互连寄生进行统计建模，则上述对变化的建模是可行的。除延迟外，还对单元输入端的引脚电容值也进行了统计建模，这意味着时序模型是根据工艺参数（全局和局部）的均值和标准差来描述的，而互连电阻和电容是根据互连参数的平均值和标准差来描述的。延迟计算过程（在第5章中介绍的）会先获得每个时序弧（单元以及互连走线）的延迟，然后再用相对于各种参数的平均值和标准差来表示。因此，每个延迟都由平均值和$N$个标准差来表示（其中$N$是统计建模中独立工艺和互连参数的数量）。

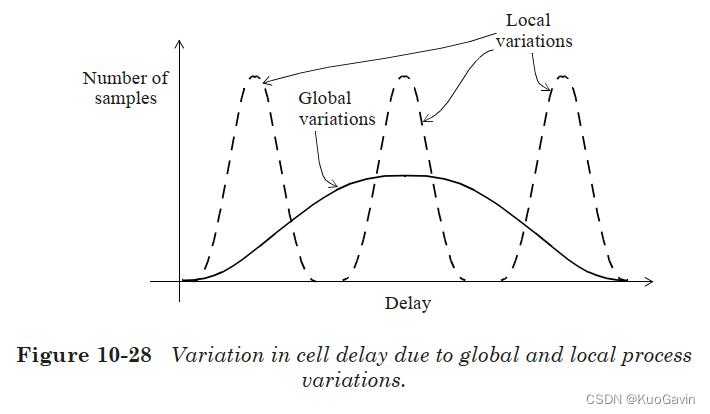
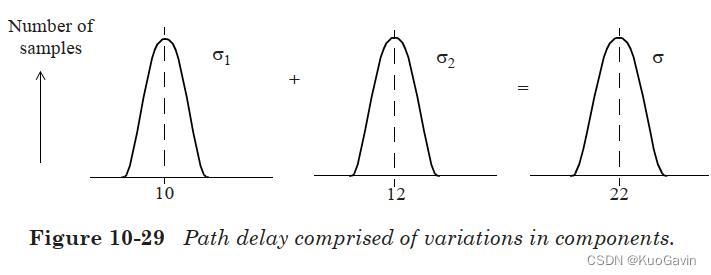
由于通过各个时序弧的延迟是用统计形式表示的，因此统计静态时序分析$SSTA$（Statistical Static Timing Analysis）过程中会结合时序弧的延迟以获得路径延迟，该路径延迟同样会以统计形式表示（具有均值和标准差）。$SSTA$会根据独立的工艺和互连参数的标准差，来获得路径延迟的总体标准差。例如，考虑由两个时序弧组成的路径延迟，如图10-29所示。由于每个延迟分量都有其变化，因此根据变化是相关的还是不相关的，将对变化进行不同的组合。如果变化来自同一来源（例如，由相互影响的$g\_par1$参数引起），则路径延迟的$\sigma$仅等于（${\sigma }_1+{\sigma }_2$）。但是，如果变化是不相关的（例如由于$l\_par1$参数），那么路径延迟的$\sigma$等于 $\sqrt{{\sigma }_1^2+{\sigma }_2^2}$，该值小于（${\sigma }_1+{\sigma }_2$）。当对局部（不相关的）工艺变化建模时，路径延迟$\sigma$较小的现象也称为各个延迟变化的统计抵消（statistical cancellation）。

对于一个真实设计，相关和不相关变量均进行了建模，因此需要适当组合这两种类型变化的权重。

发起和捕获时钟的时钟路径延迟也以相同的统计形式表示。基于数据和时钟路径延迟，可以将裕量（slack）作为具有标准值和标准差的统计量。

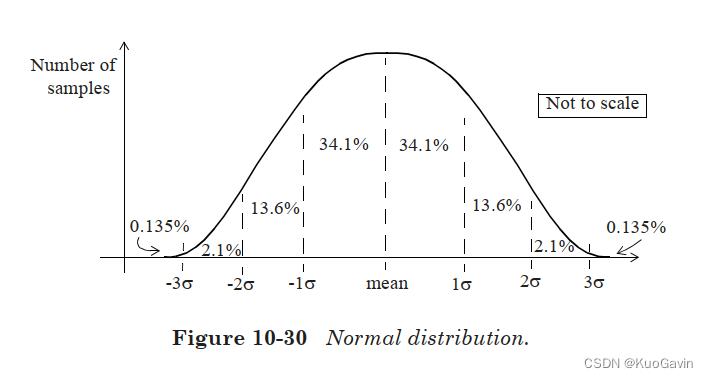
假设使用正态分布，可以获得对应于（平均值$mean+/-3\sigma$）的有效最小值和最大值。 （平均值$mean-/+3\sigma$）对应于图10-30中所示正态分布的$0.135％$和$99.865％$的分位数。$0.135％$的分位数意味着仅$0.135％$的结果分布小于此值（平均值$mean-3\sigma$）；同样，$99.865％$的分位数表示$99.865％$的结果小于此值，或仅$0.135％$（$100％-99.865％$）的结果大于此值（平均值$mean+3\sigma$）。有效的下限和上限在$SSTA$报告中称为分位数（quantile），设计人员可以选择分析中使用的分位数，例如$0.5％$或$99.5％$，对应于（平均值$mean-/+2.576\sigma$）。

对于噪声和串扰分析（第6章），将使用相对于各种参数的平均值和标准差来对路径延迟和时间窗口进行统计建模。

根据路径裕量分布，$SSTA$会报告每个路径裕量的平均值、标准差和分位数，从而可以根据所需的统计置信度（confidence）来判断时序是通过还是违例。

统计时序库(Statistical Timing Libraries)

在$SSTA$方法中，标准单元库（以及设计中使用的其它单元库）提供了各种环境条件下的时序模型。例如，在最小$V_{dd}$和高温角下进行的分析利用了在此条件下表征的库，但对工艺参数进行了统计建模。该库包含了用于标准参数值以及参数变化的时序模型。对于$N$个工艺参数，在$0.9V$电源和$125°C$条件下表征的统计时序库可能包括以下内容：

• 具有标准工艺参数的时序模型；
• 参数$i$为（标准值$+1\sigma$）的时序模型，其他参数保持为标准值；
• 参数$i$为（标准值-1σ）的时序模型，其他参数保持为标准值；

对于仅具有两个独立工艺参数的简化情况示例，时序模型是以标准参数值以及参数值的变化来表征的，如图10-31所示。

统计互连变量(Statistical Interconnect Variations)

每个金属层有三个独立的参数：

• 金属刻蚀：这可以控制金属宽度以及与相邻导体的间距。金属层中的大刻蚀减小了宽度（这增加了电阻）并增加了到相邻走线的间距（这减小了到相邻走线的耦合电容）。该参数表示为导体宽度的变化；
• 金属厚度：较厚的金属意味着与下面各层的电容更大。该参数表示为导体厚度的变化；
• $IMD$（金属间介电层）厚度：较大的$IMD$厚度会减少与下面各层的耦合。该参数表示为$IMD$厚度的变化。

SSTA结果

统计分析中输出的结果将根据平均值和角的有效值来提供路径的裕量。以下是用于建立时间检查（最大路径分析）的$SSTA$报告示例：

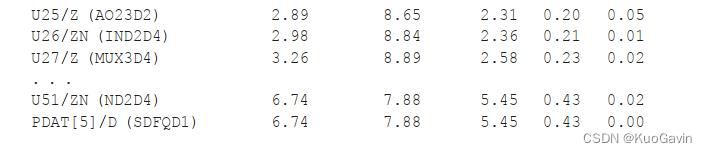
上面的报告显示，尽管时序路径的均值满足要求，但$0.135％$的分位数却有 0.43