图像处理之《基于生成对抗网络和梯度下降逼近的鲁棒无覆盖隐写术》论文精读

Posted 2022-12-15 Hard Coder

一、相关知识

1、图像隐写术分类

本文对图像隐写术又做了新的分类，可以分为传统图像隐写术、无载体图像隐写术和基于深度学习的图像隐写术。

本文又将基于深度学习的图像隐写术又分为四种：基于嵌入的方法(即将传统的隐写术如LSB与生成模型相结合，以提高抵抗隐写分析的能力)、基于融合的方法(即通过神经网络将秘密数据和封面图像融合)、基于映射的方法(建立秘密数据与图像的映射关系，利用神经网络提高嵌入效率和反隐写分析能力)和基于生成的方法(即使用GAN或GAN的变体根据秘密数据生成隐写图像，本文是一种基于生成的方法)。

其实，我们可以看出这样对图像隐写术分类不太合理，因为很多文章都是基于深度学习的无载体图像隐写术。

2、GAN的发展历程

GAN 我们已经非常熟悉，但其存在训练的不稳定性。有学者通过引入 Wasserstein 距 离 和1-Lipschitz 对其进行改进得到 WGAN。但 WGAN 在处理 1-Lipschitz 时直接使用权值裁剪，会导致参数集中和参数调优中的梯度爆炸或消失，又有学者通过引入满足 1-Lipschitz 的梯度惩罚，训练不稳定、梯度消失和模式崩溃等问题得到 WGAN-GP，即本文所使用的神经网络架构，但本文只是用它进行预训练，我们不过多进行说明。

3、梯度下降算法

本文所使用核心思想就是梯度下降算法，其实它本质上很简单，就是不断迭代逼近我们想要的值。

如果我们需要确定方程 g(x)=C 的根，就可以使用图中公式进行梯度下降求解。首先给 x 取一个粗略的近似值，设置迭代步长 r，对 f(x)的 x 求偏导，然后开始不断迭代修正初值，直到达到预定的精度要求。

我们看个实际例子，比如求解公式 0.5(x-0.25)^2=0.5，显然其解是 1.25，我们根据公式得到 f(x)，此处设置的步长 r 是 0.005，初值为 4，迭代次数是1000 次。我们可以从这个示意图和控制台输出的结果可以看出，最终的结果在无限接近 1.25，但是还没有完全达到 1.25，存在误差。

二、基本思想

1、提出图像隐写的框架

本文提出的基本隐写框架，第一部分是准备阶段，使用刚才说的 WGAN-GP 进行预训练，直到可以生成器可以生成自然逼真图像为止。

第二部分是数据隐藏阶段，将秘密信息 S 映射成噪声向量 zstego，中间需要进行一个后处理，再将其输入训练好的生成器中生成隐写图像 stego。

第三部分是数据提取阶段，首先需要对隐写图像 stego 进行预处理，然后使用梯度下降更新迭噪声向量 z，直到生成器迭代生成的 G(zed)约等于隐写图像 stego。此时可以认为最终的噪声向量 zed 约等于 zstego，利用逆映射规则求出秘密信息 S’。

我们追求的最终目标就是迭代生成的图像与隐写图像相似，迭代到最后的噪声向量 zed 与原始噪声向量 zstego 相似，提取的秘密信息 S’和原始秘密信息 S 相同。

2、映射规则

本文主要使用格雷码作为映射规则，格雷码的定义是：一个长度为 2^n的序列，序列中无相同元素，且每个元素都是长度为 n 的二进制位串，相邻元素恰好只有 1 位不同。从这个表可以看出，比如 000 与 001 有一位不同，001 和 011 有一位不同，与定义相对应。

下面重点看一下格雷码与二进制之间的转换关系，主要是通过异或运算进行转换。从二级进制最高位开始，保留二进制最高位作为格雷码最高位，最高位和第二高位进行异或运算得到格雷码第二个高位，由此类推即可得到二进制对应的格雷码。

对于格雷码转二进制，是刚才的逆过程，从格雷码最高位开始，保留格雷码最高位作为二进制最高位，最高位和第二高位进行异或运算得到二进制第二个高位，由此类推即可得到格雷码对应的二进制。

我们具体本文提出的映射规则的具体步骤，第一步我们需要将秘密信息 M 分成 2^λ个段 mi，每段长度为λ,符合格雷码的定义。第二步将每一个分段视为一个格雷码，计算相应的格雷译码，但注意此处是二进制转格雷码的操作，我们刚才已经说明。第三步，噪声向量 z 按上面这个公式计算，将第二步计算的格雷译码代入即可。

这两个表是取λ=3 时的映射规则和逆映射规则。从上面这个表可以看出每个秘密信息段 mi，对应一个 zi 值；从下面这个表可以看出在提取秘密信息时，只要提取的 zi 位于正确的范围内，就可以恢复正确的 mi。因为图像在传输过程中会受到攻击，所以在隐写图像中提取数据时允许有偏差容忍表现为这里的 zi 是一个范围而不是具体某个值。

我们可以简单验证一下这两个公式，当 mi=100 时对应的格雷译码为111，对应十进制为 7，代入公式可以得到 0.875，即 100 对应 0.875。当 zi=0.8, 属于 0.75-1.00 区间，通过下面公式可以计算出格雷为 100，即 0.8 对应 100。

3、数据隐藏

首先利用前面说明的映射规则将秘密信息分段映射成噪声向量 zstego，在生成器输入 zstego 会生成 rawimage 矩阵，该矩阵范围限制在[-1,1]。最后对 rawimage 矩阵经过一个后处理将其范围变换到[0,255]。

我们可以简单验证一下这个公式，假设 rawimage 矩阵一个值为-1，代入公式为 0；假设 rawimage 矩阵一个值为1，代入公式为 255，即 stego的范围为[0,255]。

4、数据提取

首先需要对刚才生成的 stego 进行预处理，将从区间[0,255]转换为[-1,1]的 target 矩阵。现在我们来对比数据隐藏阶段的后处理和数据提取阶段的预处理，理论来说，它们是一个互逆的过程。

对预处理公式进行变换得到公式 1，对比后处理的公式 2。我们通过举例验证：当 target 矩阵和 rawimage 矩阵中一个值为 0.01，将其代入公式 1 和 2，可以得到公式 1 值为 128.775(注意像素值为整数)，公式2 值为 129，显然不相等。故此处公式有误，需要加上向上取整符号。

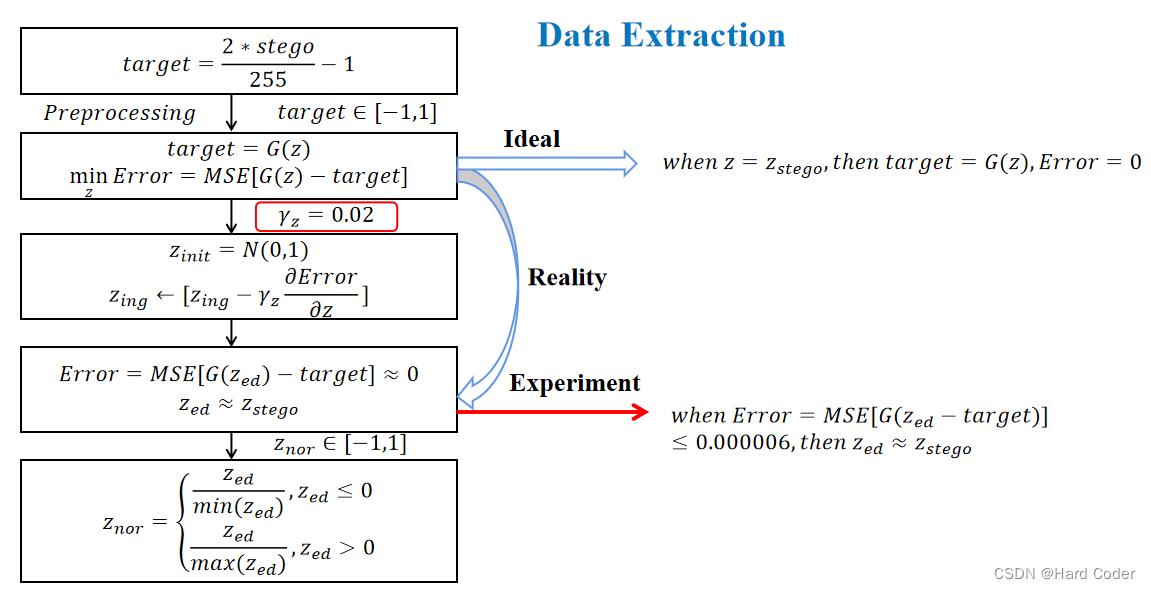
第二步是求解方程 target = G(z)，利用梯度下降算法迭代更新噪声向量 z 的参数，使误差函数值最小。在理想情况下肯定是当 z = zstego 时，target = G(z)，Error = 0。

对 z 的初始值是从标准正态分布中随机抽取一个向量，输入到生成器中迭代更新，迭代过程中 z 值的变化公式如图所示，rz 是步长，实验部分设置为 0.02。

当误差下降到一定程度时，生成器将输出一个与隐写图像非常相似的图像，噪声向量 zed 也与隐写噪声向量 zstego 高度相关。文章实验部分设置了一个允许误差为 0.000006，当 Error≤0.000006 时可以认为 zed≈zstego。

因为第三步是从标准正态分布中随机抽取一个向量，作为 z 的初值，难免会取到[-1,1]区间之外的值，所以需要进行归一化处理，将 z 的值限制在[-1,1]内方便我们使用逆映射规则提取秘密信息。

我们通过一个实际例子来理解一下这个归一化公式，显然 min(zed)是小于 0 的，max(zed)是大于 0 的。假设 z 的最小值为-1，z 的最大值为 1。当 zed=0 时，归一化后值为 0；当 zed=1 时，归一化后值为 1；当 zed=-1 时，归一化后值为 1。显然文章给的归一化公式有问题，当 zed≤0 时，分母应该是 z 的最大值。

三、实验结果

本文的实验内容比较丰富的，我们挑其中四个重点内容看一下：提取精度分析，容量分析，鲁棒性分析和提取机制的对比。

1、提取精度的分析

文章设置λ=1,2,3,4,5,6,7，进行了 7 次实验，求出每一次的提取精度。提取精度的计算公式如图所示，通过汉明距离比较提取的二进制秘密信息和原始二进制秘密信息，再用 1 减去所占比例，最后将 100 个二进制秘密信息的提取精度求和取平均到平均的提前精度。

通过这个表可以看出当λ = 1，2，3 时，所提方案可以完全提取秘密数据，即使λ = 7，提取精度也可达到 92.21%。同时我们也看一下每个λ 对应的容量是 nz*λ，文章中实验部分取 nz 为 256，可以知道二进制秘密信息必须是 256 的倍数才可以。

2、容量分析

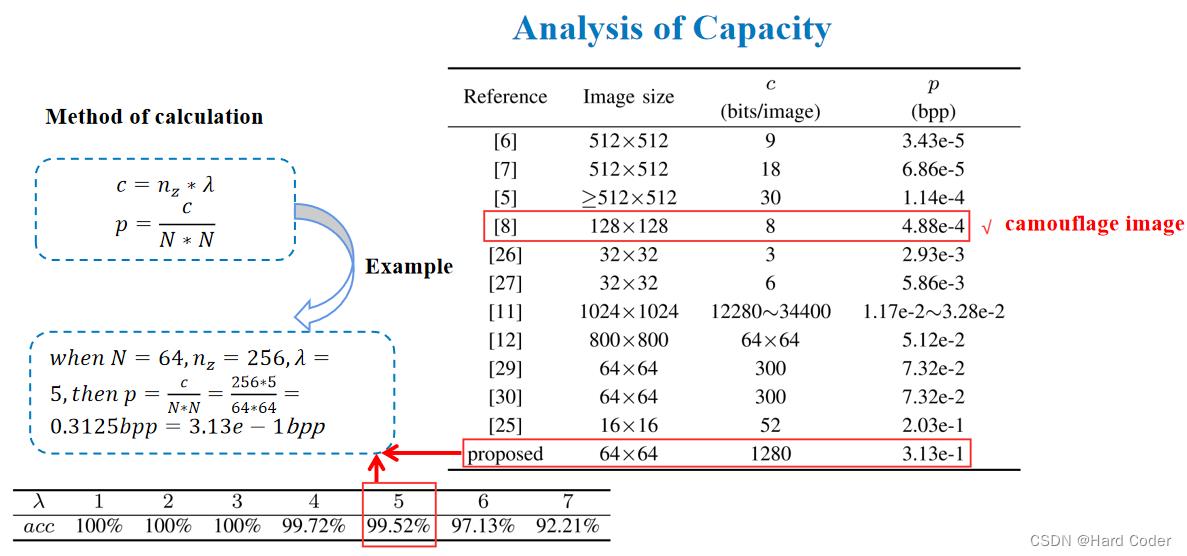
当λ = 5 时，提取精度高于λ = 6，7 时，非常接近 100%。同时，λ = 5 的容量远大于λ = 4 的容量，所以文章中取λ = 5，图
像大小 N 为 64，噪声向量 nz 维数为 256，将此时的有效载荷视为最佳，可以计算得出约等于 0.313bpp。从右边这个表页可以看出，本文提出的方法有效载荷最高。

3、鲁棒性分析

本文在前人的基础上又增加了两个攻击一个是区域随机掉落，一个是扭曲，效果如图 j 和 l 所示。

对于中心裁剪、边缘裁剪和区域随机掉落攻击，从这幅图可以看出图像中出现很多黑色区域，三个通道被攻击像素的值都为 0，原始图像信息已经完全丢失，将被攻击的图像作为隐写图像进行迭代意义不大。

所以本文提出一种掩膜方法，将一个 NN3 的零矩阵 zeros 与被攻击的隐写图像 stego’作异或运算，得到一个 mask 矩阵，显然 mask 是 0 和 1 组成的，其中 0 表示无效像素，1 表示有像素，因为异或运算相同为 0 不同为 1，用于消除被攻击像素的干扰。再将 mask 与生成图像、被攻击隐写图像作点乘运算做差作为 Error 求出最小值时的 z，即可以做到即使被这三种攻击后的隐写图像，我们也可以生成与其最相似的图像，如右图所示。

下面是一个简单例子来说明公式含义。我们此处以一个通道3*3 像素块为例。

4、提取机制的比较

上面这个表中：文献 29 和 30采用训练 CNN 提取器提取秘密数据，在实验设置与本文所提方法相同的情况下，提取精度非常低。第三列是采用自然二进制作为映射规则，可以看到随着λ增大，与格雷码作为映射规则相比，提取精度下降比较快。

下面这个表继续与其他文献作对比，可以看出本文提出的梯度下降方法的计算开销比较低，提取精度比较高，鲁棒性比较强且隐藏容量适中。

四、文章创新点与不足

1、创新点

2、不足

论文地址：A Robust Coverless Steganography Based on Generative Adversarial Networks and Gradient Descent Approximation