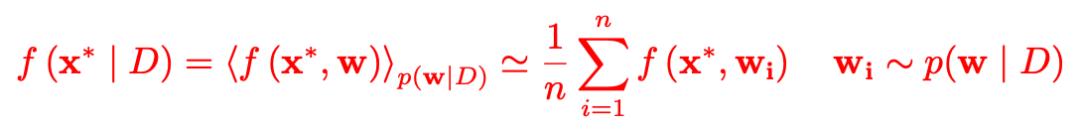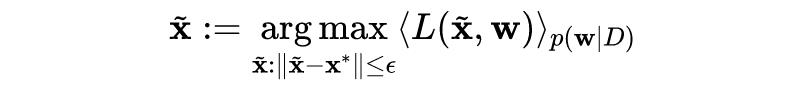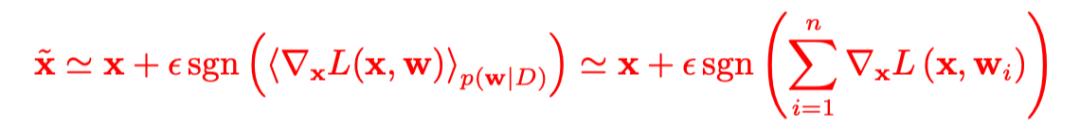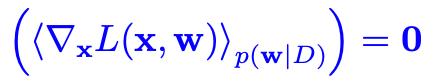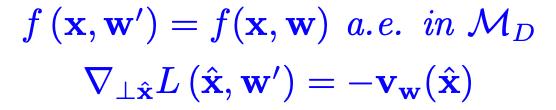贝叶斯神经网络对梯度攻击的鲁棒性
Posted PaperWeekly
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了贝叶斯神经网络对梯度攻击的鲁棒性相关的知识,希望对你有一定的参考价值。
©PaperWeekly 原创 · 作者|尹娟
学校|北京理工大学博士生
研究方向|随机过程、复杂网络单位

引言
贝叶斯神经网络(BNN)在最近几年得到了一定的重视,因为其具有一定的推断能力。BNN 不同于一般的 DNN,其权重参数是随机变量,而非确定的值,它是通过概率建模和神经网络结合起来,并能够给出预测结果的置信度。
其先验用来描述关键参数,并作为神经网络的输入。神经网络的输出用来描述特定的概率分布的似然。通过采样或者变分推断来计算后验分布。这对于很多问题来说非常关键,由于 BNN 具有不确定性量化能力,所以具有非常强的鲁棒性。
本文分析了贝叶斯神经网络对对抗攻击具有一定的鲁棒性并且分析了在大数据量、过参数极限下的对抗攻击的几何结构。
并且作者证明了,在一定范围内,由于数据分布中的简并性(高维数据可以映射到低维流形上),当数据位于环境空间的低维子流形上时,基于梯度的攻击的脆弱性就会出现,并且本论文提供了相关的代码,最后一部分会介绍相关的代码。

论文标题:
Robustness of Bayesian Neural Networks to Gradient-Based Attacks
论文链接:
https://arxiv.org/abs/2002.04359

论文的贡献
-
作者提出了在大数据限制下 BNNs 对抗鲁棒性分析的理论框架,该理论框架也是该论文的核心贡献。
-
作者证明了在损失函数梯度的后验平均值为零的情况下,贝叶斯神经网络会对基于梯度的攻击的具有一定的鲁棒性,论文中的定理,引理和推论都以此展开。
-
该论文是一篇理论和实验相对严格的文章,实验表明 BNN 对基于梯度的攻击具有鲁棒性,能够抵抗已知的精度鲁棒性权衡,与作者的证明很好的切合。
模型介绍
论文作者通过理论推导和大量的实验证明了贝叶斯神经网络具有一定的鲁棒性,网络本身就可以抵御一定的对抗攻击,并且提出了攻击贝叶斯神经网络的方法 FGSM(类似于攻击传统神经网络的 FGSM),类似的还有 PGD 和 MIM 等迭代的攻击。
3.2 贝叶斯网络
贝叶斯模型可以通过预测器的集合来捕捉数据驱动模型的内在认知下的不确定性;它通过将算法参数(以及相应的预测)转化为随机变量来实现。在神经网络中,对于具有输入
和网络权重参数
的神经网络
,则从网络权重
的先验度量开始。通过似然
评估权重为
的网络与数据
的拟合度。
贝叶斯推理通过 Bayes 定理将似然和先验相结合,得到权重空间
的后验测度。神经网络的标准训练可以看作是贝叶斯推理的一种近似。对于 NNs 这样的非线性/非共轭模型来说,精确地获得后验分布是不可能的。
后验分布的渐近精确样本可以通过蒙特卡洛模拟来获得,对于一个新输入的样本
贝叶斯预测都是从 n 个神经网络的集合中获得的,每个神经网络的权重都来自于其后验分布
:
论文中这这部分作者没有详细展开说明,不过可以从公式可以推测出来
表示的是已知训练数据集的情况下,贝叶斯神经网络给出的样本
的预测,
表示是不同权重参数的给出预测的期望,然后用蒙特卡洛模拟将期望形式转化成离散的平均加和的形式。
3.3 对抗攻击
给定样本点
和攻击强度(也是攻击扰动量)
,则生成对抗样本 x 的目标函数为:*
要知道
是非线性非凸的,基于梯度的一阶攻击方法是一种高效的求解方式,与 Goodfellow 提出的生成传统对抗样本的 FGSM 方法的原理相似,论文作者提出了相类似的贝叶斯神经网路生成对抗样本的方法,具体形式如下所示:
类似的还有 PGD 和 MIM 等迭代攻击的形式,本文着重讲解有关 FGSM 的相关算法。
3.4 贝叶斯神经网络对抗鲁棒性
本文这一部分会涉及到一个定理,两个引理和一个推论,其中心思想突出的是贝叶斯神经网络具有一定的鲁棒性并分析了数据流形和对样样本之间的关系,作者提出了针对贝叶斯神经网络的对抗攻击。
直观上 BNN 对抗性攻击的鲁棒性的一个可能的解释是后验下的平均值可能导致梯度的最终期望值为 0。这种平均特性与所谓的数据流形几何结构密切相关。作者证明了随机梯度下降法(在分布水平上)在过参数、大数据极限下的可以全局收敛性。
定理1:
令
是一个训练完全,过参数化的贝叶斯神经网络,其中该网络的样本数据流形为
,先验权重参数为
。假定
处处存在,在大数据的极限下,会有如下形式:
定理 1 说明在网络结构和数据量高精度和强表达的情况下,BNN 梯度的平均效应对网络具有一定的保护作用。随着网络参数和训练输入数目的增加,梯度期望值的大小会减小。
定理 1 是在一致先验假设下被证明的;我们可以观察到定理中提及了在大数据的极限下这个条件,换言之如果突破这个极限,与理想情况会有一定的偏差。
引理1:
令
是一个训练完全,过参数化的贝叶斯神经网络,其中该网络的样本数据流形为
,先验权重参数为
。
令
,则
表示以
为中心,
为半径的多维球体,那么
对基于梯度攻击有强度
的鲁棒性。
引理 1 说明了当在目标函数收敛时,过参数神经网络可在无限数据极限下对整个数据流实现零损失,这意味着函数
将在
处局部恒定,所以贝叶斯神经网络
可以抵御一定程度的对抗攻击。
推论1:
令
是一个训练完全,过参数化的贝叶斯神经网络,其中该网络的样本数据流形为
,并且数据分布平滑的。如果
在样本点
受到对抗攻击的数据维度为
。
推论 1 说明了对抗性攻击可能源于数据流形的退化。事实上 Goodfellow 曾经提出过对抗性的扰动会出现在与数据流形垂直的方向上。嵌入空间中数据流形的余维越高,对抗样本就越有可能存在于与其垂直的随机方向上。
引理2:
令
是一个训练完全,过参数化的贝叶斯神经网络,其中该网络的样本数据流形为
,先验权重参数为
。样本
由概率梯度
所攻击,在无限数据的极限下,对于几乎所有的
,存在一组权重
,使得:
引理 2 说明可以通过求出目标函数的概率梯度,以此适当地局部扰动完全训练的神经网络
,以达到攻击贝叶斯神经网络的目的。

实验结果
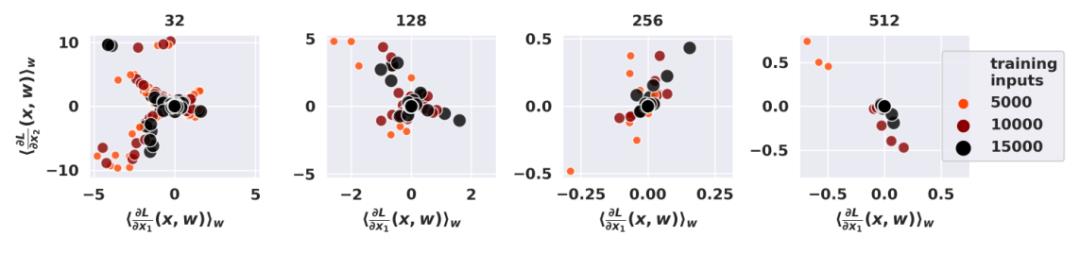
下图表示的是在半月数据集(头一次听说)中 100 个二维测试点上的预期损失梯度分量(其显示了损失函数的两个偏导数)。每个点代表不同的神经网络架构。作者使用了一组 HMC-BNN(HMC 表示的是蒙特卡洛模拟),通过改变隐藏神经元的数量和训练点。
论文只考虑了模型测试精度大于80%的情况。可以观察到当损失梯度趋于零时,训练点数量和参数数量不断增加,随着从
的后验分布中提取的样本数量增加,梯度的所有分量都接近于零,实验结果与定理 1一致,只有通过集合预测器的贝叶斯平均,梯度才能被抵消趋近为 0。
下图为 MNIST (顶行)和 Fashion MNIST(下一行)的示例图像及其与 HMC(左)和 VI(右)训练的网络的期望损失梯度。在图像的右侧,还绘制了渐变值的热图。下图说明当从后验预测分布中增加样本数时,贝叶神经网络的期望损失梯度呈现消失行为。

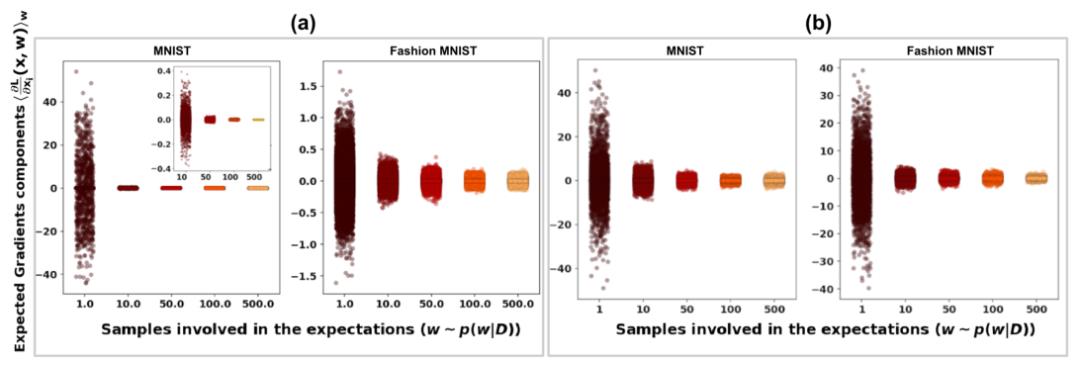
下图显示了来自 MNIST 和 Fashion MNIST 数据集的 1000 个不同测试图像的 784 个梯度分量。梯度是在 HMC(a)和 VI(b)训练的贝叶斯神经网络上计算的。对于 HMC 和 VI,梯度分量的大小随着样本数量的增加而下降,并且在从后验分布中抽取 100 个样本时趋于稳定在零附近,这表明作者分析的 BNN 近似满足定理 1 中规定的条件。在 HMC 训练的网络上计算的梯度更快地降到零。
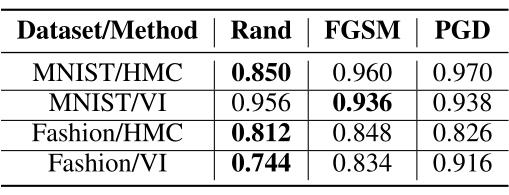
下表表示了在 HMC 和 VI 训练的 BNNs 对随机扰动攻击、FGSM 和 PGD 的对抗鲁棒性,其中为 500 幅图像的对抗准确度(即网络返回干扰输入的真实标签的概率)。
对于每个图像,作者使用 250 个后验样本计算期望的梯度。对于所有攻击,作者都使用了与训练过程中使用的可能性相关的分类交叉熵损失函数。可以观察到随机攻击优于基于梯度的攻击,说明梯度的消失行为使得 FGSM 和 PGD 攻击失效。
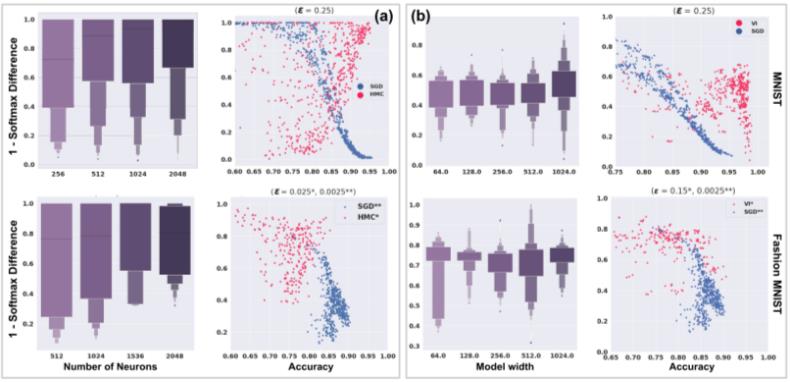
下图为使用 HMC(a)、VI(b)和 SGD(蓝点)训练的贝叶斯神经网络在 MNIST(第一行)和 Fashion MNIST(第二行)上的稳健性-准确性示意图。HMC 上的实验表明精度和鲁棒性之间存在正相关关系。箱线图显示了模型容量和鲁棒性之间的相关性。
对于用 VI 训练的贝叶斯神经网络,鲁棒性似乎与准确度呈负相关。可以观察到模型大小有一些变化趋势,仅在使用 MNIST 训练的情况下观察到这一点,在这种情况下,模型鲁棒性可能会随着层宽度的增加而增加,但这也会导致鲁棒性差(这可能表示模式崩溃)。

总结思考
贝叶斯神经网络兴起的原因不仅在于其可以通过学习训练数据进行推理而且在于贝叶斯网络训练的模型比传统训练网络训练的模型更具鲁棒性,可以抵御一定的对抗攻击。
读完该论文自己一直有一个问题,论文中定理,引理还有推论中提及的那个条件“在大数据的极限下”,这个极限到底是多少,换言之如果突破这个极限所有的定理,引理还有推论都不成立,作者也坦言也不是很清楚自己论文中的实验数据量离这个极限有多近。
不过该论文相对严格的给出了他的证明和实验,并且突出了对抗的脆弱性和数据流形几何结构之间的深刻联系;正是这种联系能够证明,原则性随机化可能是在高维环境下提供鲁棒性的有效方法,为未来提供了以较低的计算成本对模型进行对抗保护的研究方向。