基本矩阵F与本质矩阵E的分析与计算
Posted
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了基本矩阵F与本质矩阵E的分析与计算相关的知识，希望对你有一定的参考价值。
参考技术A 对于这三个矩阵还有坐标系什么的真是看了忘，忘了看，今日索性一次性将它记下来，下次再忘的时候翻看一下就行了。如果直接将胶片放置在物体前面，由于光的折射，反射等等现象，在胶片上是成不了像的。但是在物体和胶片之间放上一块挡板，挡板上有一个小孔，它阻挡了大部分的光线，就将这个屏障上的小孔称之为光圈，胶片上就获得了倒立的图像。但是，这个小孔成像存在一个问题，就是，光圈越小曝光时间越长，形成高亮度的图像，，而且太小了，就会产生光的衍射现象，图像也模糊了，光圈大虽然曝光时间短了，可图像变模糊了。对于这样子的相机来进行实时的特征提取等等显然是行不通的，所以就有了透镜系统。在光圈之前加凸透镜，众所周知，凸透镜具有聚焦的功能，这样，成像的速度加快了许多，只需要差不多0.01秒。
当相机为单目的时候，只知道2D的像素坐标，需要通过两视图来估计相机的运动。假设从两张图像中得到了一对匹配好的特征点，如果有若干对这样的匹配点，就可以通过这些二维图像点之间的对应关系，恢复出两帧之间摄像机的运动。两视图的对极几何约束可以用基本矩阵F表示，那么如何得到这个矩阵呢?
首先说明一些术语，O1和O2称为光心，O1、O2和P构成的平面称为极平面，p和e1，q和e2称为极线，e1和e2为O1和O2与像素平面的交点称为极点。可以知道的是由于他们都在同一平面上，所以q点的投影必然在pe1这条极限上，而同理p的投影也必然在qe2上（针对于像素平面）。矩阵F表示了第一帧的像素点p与第二帧的像素点q极线之间的映射关系。如何得到F和E，有以下两种方法：
方法一：
这里需要引用两个点的齐次坐标叉乘能够表达一条直线l的系数。可以对其进行证明（ 两点的叉乘表达一条直线 ），直线的方程可以表示为 ，所以该直线可以用向量 进行表示。e2是光心O1在第二帧上的投影，假设光心O1的齐次坐标为 ，转到光心O2的坐标为 ，将O2投影到相机平面，则e2的坐标为 ，q的齐次坐标为 。又因为 所以直线qe2可以表示为 ，由于这里p和q的坐标都用齐次坐标表示，那么（这里的"="是在相差尺度系数的情况下成立的）：
设 和 是归一化平面的坐标，所以：
，
(1)
所以 ，又因为q在直线上，那么 ，
由于K是3*3的矩阵，[R|t]是4*4的矩阵，将K进行扩展第4行第4列为1之外，第四列的其他值均为0，所以对于[R|t]来说，t的值已经对结果没有影响了，所以上式就变成 ，将 代入，得：
又有 ，所以
且 。
方法二：
将（1）式叉乘t，可以得到： ，再将其乘以 ，由于 是一个与t和x2都垂直的向量，所以左边为0，有;
，代入p，q，得 ，综上所述：
，
由于 ，F的秩为2（原因是因为 的秩为2），自由度为7（尺度等价性），使用直接线性变换8点法来进行计算。具体推导出来的就不写了，直接得出 ，A是一个8*9的矩阵， 就是将F矩阵展开的向量。
A中的一行为： ，一共需要8组匹配点
为：
计算过程：
（1）构造得到 ;
（2）对A进行SVD分解。由于A的秩是8（忽略特征点在同一个平面上的情况），那么它的对角矩阵的值为 ，而 ，右乘 得到 （U和V都是正交矩阵，转置就是它的逆），其列向量形式为：
求得的刚好是Af=0，为了求得F只要取V的最后一列就能构造了。
（3）但是，从上面构造的F可能是满秩的，所以需要进一步的求解，将上面构造的F进行SVD分解， ，现在求得的 值应该是有三个大于0的数，由于秩为2，应该将最后一个特征值置为0，为：
最终的F就等于最后一个特征值置为0对角矩阵乘以U和V，为 。
可以通过基本矩阵F得到本质矩阵E， ，也可以通过构造和基本矩阵一样的八点法来得到。由于 ，t有3个自由度，R也有3个自由度，那么它应该有6个自由度，又因为E的尺度等价性，所以E只有5个自由度。
对E进行奇异值分解相当于对 与 的乘积进行分解，乘积奇异值分解有个性质是任何一个矩阵A与正交矩阵相乘，其奇异值保持不变，证明：
由于奇异值是通过计算 的特征值得到的，那么 ，所以奇异值不变。
设 ，
由于 为反对称矩阵，可以证明任意的反对称矩阵都可以用 来表示，又有：
所以 ，则本质矩阵就可以写成 （根据尺度等价性，k可以去掉），那么 ，这就可以说明E的奇异值为何是 的形式了。
知道了E的SVD分解形式，R和t也可以相应的分解出来，E和-E是等价的，所以R和t存在两组解：
，
，
最后只要把任意一点带入4种解中，检测该点在两个相机下的深度，就可以确定哪个解是正确的了。
先就写这些吧，之后遇到什么不会或是容易忘记的再补充。
《视觉SLAM十四讲》 高翔
《矩阵分析与应用》 张贤达
直观详解线性代数的本质
目录
前言
【阅读时间】1小时左右 words 14069words
【内容简介】将只停留在数值运算和公式的线性代数推进到可视化几何直观（Visual Geometric Intuition）的领悟上，致敬3B1B的系列视频的笔记，动图也都来自于视频。内容涉及到基变换，叉积，逆矩阵，点积，特征向量与特征值。每一章节都有一句经典的名言，非常有启发性。
在笔记开始之前，想象学习一个事物（概念）的场景：我们需要学习正弦函数，sin(x)，非常不幸的是，你遇到了一本相当装逼的教材，它告诉你，正弦函数是这样的：
的确很厉害的样子，并且，计算器就是这样算 sin(x)，知道了这个的确“挺酷的”。对你来说，你的作业可能就是回家把代入到公式里面，发现，好神奇！竟然越算越接近
0.5。此时你对sin(x)与三角形之间的几何直观只有一些模糊的概念。这样的学习过程就十分悲催了。为什么呢？
再假设一个场景，接下来，物理课，正弦函数随处可见，下图场景中，其他人能快速的大概估计出这个值是0.7。而刚“学过”正弦函数的你，内心戏可能是这样的：这些人忒diao了吧？你莫不是在玩我？
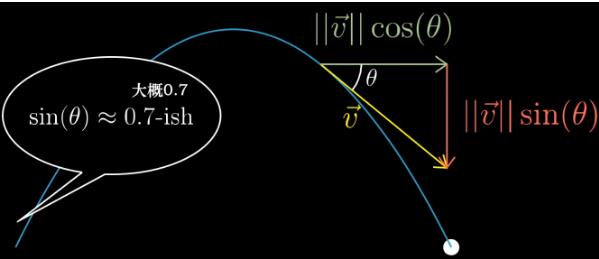
你可能会觉得这些做物理的人脑子也太强了，我弱爆了。其实，你需要只是一个几何直观的灌输而已，这也从侧面佐证了一个好的老师（这里的好老师真的不是他本身的学术能力有多强，而在于他擅不擅长站在学习者的角度不断的修正教学方法。甚至，模拟学生的学习过程提前预知所需要的基础概念）是有多么重要。
教学不同层次的人：初学，入门，掌握，理解，都是不同的。解释的角度，方式都完全不同。更加不幸的是，为了能更加通用的用理论来描述现实生活中的规律，人类已经做了很多工作，我们常说：越通用，越抽象（越难以理解）。这对于初学者来说堪称一段噩梦
这个例子比较极端，但只为强调一件事：直观理解很重要，或者说，学习方法很重要。好的学习方法即你如何直观的去理解（可能是几何的，或是现实中的具体例子）一个抽象的事物，并层次化的建立知识与知识间的联系，构建并健壮属于自己的知识图谱。个人观点是，这种【学习方法】是最高效的。它唯一的难度在于，需要一定的基础知识打底，一定的量变结合方法论（点拨或领悟）就是质变。换句话说，想躺着学习？不存在的
根据生物学家我们知道，人对具体的事物（动画＞图形＞数字＞未建立直观理解的文字）更敏感，记忆速度更快。这篇笔记的对象3B1B团队生产的内容目的就是从为了帮助人们建立直观概念的角度来教学，在如今中国应试教育风行的大背景下，它会超越你的认知：学习如追番般期待，真不是一个调侃！
我是极度反对现代大学的线性代数课程中（甚至数学类课程）的教学方法的，在计算上（做题）花费了大量时间。而工程中，有计算机，绝不会有任何一个人去笔算矩阵的逆或特征值。如果现在的老师反驳：做计算的目的是为了让你通过大量的联系（重复）去记牢概念，我也一直坚信：学习知识的最快捷径是带有思考的重复，但那是带思考的重复，有一些直观的方法在帮助你理解和记忆上比做题有效率的多。
注解，因为这是一篇个人笔记，我个人已经深刻理解的内容，或者我觉得是很基本的内容我会略过或默认。好消息是，我自己也是一个理解力非常捉急的人，所以还是会比较详细的
什么是矩阵？矩阵 = 变换的数字表达(或者说：矩阵就是用数字形式来表达变换)
向量究竟是什么
引入一些数作为坐标是一种鲁莽的行为 ——赫尔曼·外尔
The introduction of numbers as coordinates is an act of violence - Hermann Weyl
这部分，讲向量，扎实的读者完全可以跳过
向量的定义 What
对于向量的这个概念，大家一定并不陌生，但是这次让我们从数学，物理，计算机三个角度来看待如何定义这个【向量】这个概念
物理专业角度
- 向量是空间中的箭头
- 决定一个向量的是：它的长度和它所指的方向
计算机专业角度
- 向量是有序的数字列表
- 向量不过是“列表”一个花哨的说法
- 向量的维度等于“列表”的长度
数学专业角度
从数学来说，它的本质就是通用和抽象，所以，数学家希望概括这两种观点
- 向量可以是任何东西，只需要保证：两个向量相加及数字与向量相乘是有意义的即可
- 向量加法和向量乘法贯穿线性代数始终，十分重要
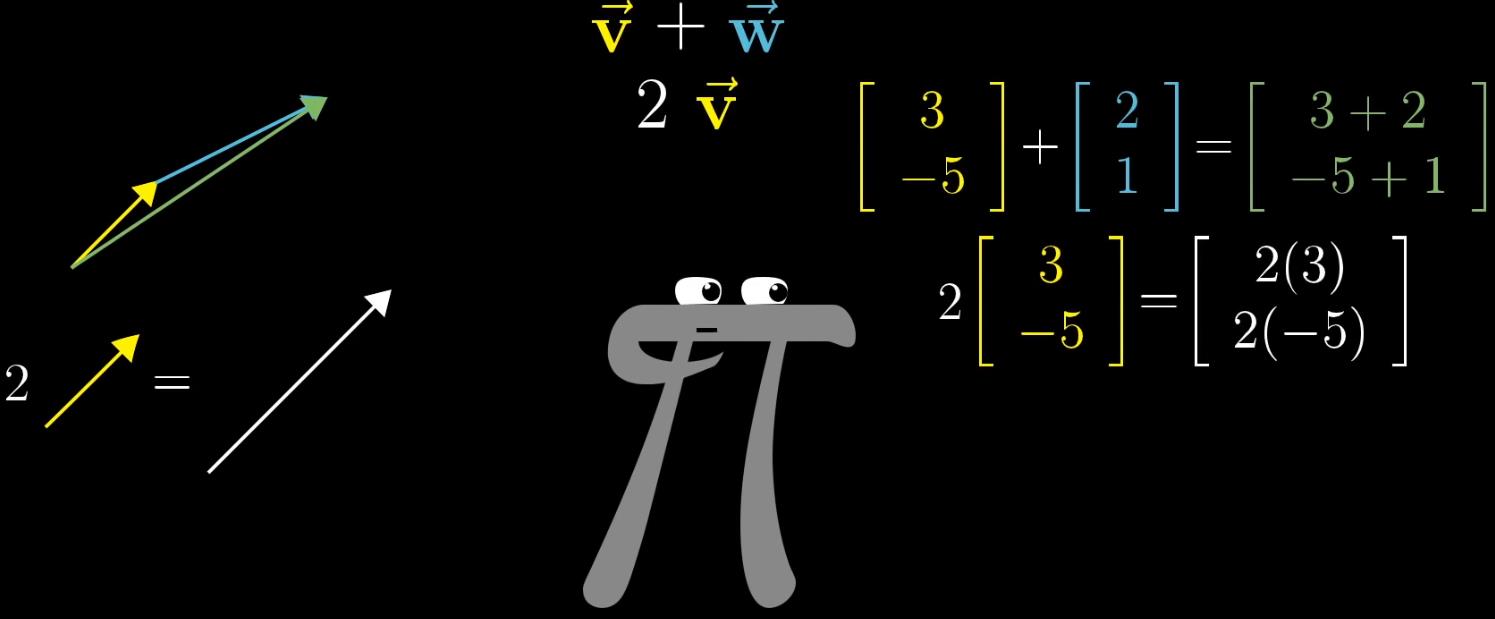
可以通过上图直观的感受到数学家（这个很牛逼的灰色的
）在想什么，有种【大道】的逼格。左边是物理角度，右边是计算机角度，但是很抱歉，我能用一些抽象的定义和约束让你们变成一个东西
坐标系
把向量至于坐标系中，坐标正负表示方向，原点为起点，可完美把两个不同的角度融合
- 向量加法
- 物理：首尾相连 Motion
- 计算机：坐标相加
- 向量乘法
- 物理：缩放 Scaling
- 计算机：坐标和比例相乘
线性组合、张成的空间与基
数学需要的不是天赋，而是少量的自由想象，但想象太过自由又会陷入疯狂 ——安古斯·罗杰斯
Mathematics requires a small dose, not of genius, but of an imaginative freedom which, in a larger dose, would be insanity - Angus K. Rodgers
本部分继续加深一个概念，为何向量加法与向量乘法是那么重要，并从始至终贯穿整个线性代数
线性组合
这个概念再好理解不过，空间中不共线的两个不为零向量都可以表示空间中的任意一个向量，（或者说：空间中的任意一个向量，都可以用[[数]乘[向量]的和]来表示。）写成符号语言就是：
至于为什么被称为“线性”，有一种几何直观：如果你固定其中一个标量，让另一个标量（数）自由变化，所产生的向量终点会描出一条直线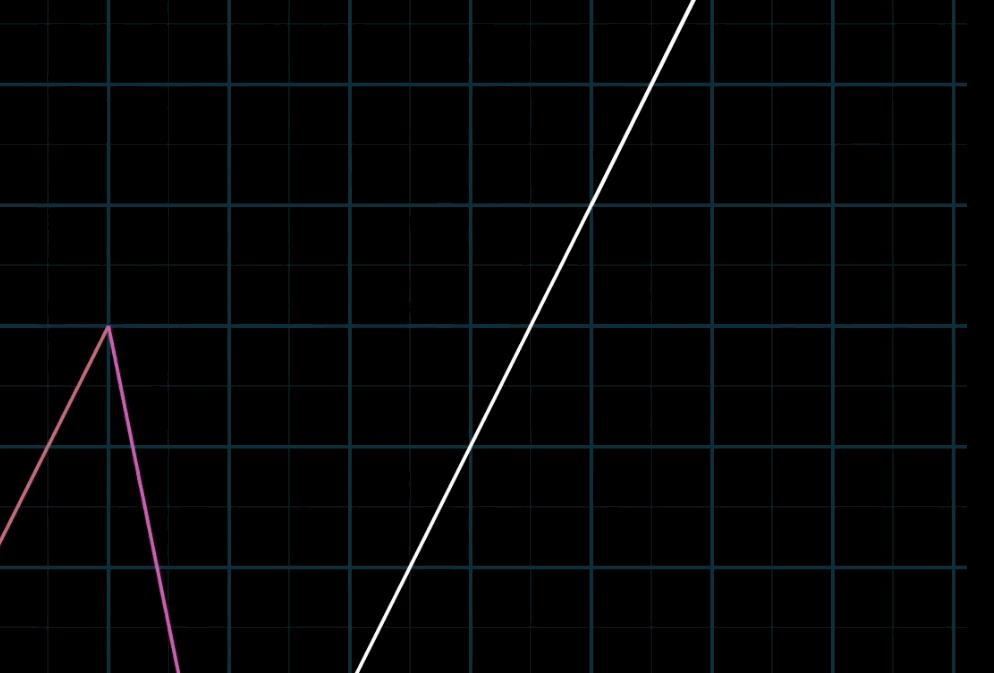
空间的基 Basis
对于我们常见的笛卡尔坐标系，有一个最直观一组基： ，即单位向量：
和
，通过
和
的拉伸与相加可以组成笛卡尔坐标系中的任意一个向量
张成的空间 Span
同理，举一反三的来说，我们可以选择不同的基向量，并且这些基向量构成的空间称为：张成的空间。张成二字比较拗口，可以类比为延展或扩展。直观来看，就是所有动图中的网格。笛卡尔坐标系就是一个由单位坐标张成的空间
所有可以表示为给定向量（基）线性组合（刚刚讲了这个概念）的向量的集合，被称为给定向量（基）张成的空间
如果你继续思考一下，会发现一个特点：并不是每一组给定向量都可以张成一个空间，若这两个向量共线（2D），共面（3D），它们就只能被限制在一个直线或面中，类似于“降维打击”。通过这个直观的思考可以引出一个概念：线性相关
线性相关
关于什么是线性相关，有两种表达
- 【表达一】你有多个向量，并且可以移除其中一个而不减小张成的空间（即2D共线或3D共面），我们称它们（这些向量）线性相关
- 【表达二】其中一个向量，可以表示为其他向量的线性组合，因为这个向量已经落在其他向量张成的空间之中
如果从统计学角度来说，这些向量之中有冗余。这一堆向量中，我们只需要其中几个（取决于维度）就可以表示其他所有的向量。
向量空间一组基的严格定义
有了这些对名次（概念）的直观理解，来看看数学家们是如何严谨的定义向量空间的一组基：
向量空间的一组基是张成该空间的一个线性无关向量集
用这样的步骤来慢慢导出这个定义，个人感觉，远比在课堂的第一分钟就将这句让你迷惑的话丢给你好的多，抽象的东西只有在慢慢推倒中你才能发现它的精巧之处，非常优雅且迷人
矩阵与线性变换
很遗憾，Matrix（矩阵）是什么是说不清的。你必须得自己亲眼看看 ——墨菲斯
Unfortunately, no one can be told what the Matrix is. You have to see it yourself -Morpheus
矩阵，最直观的理解当然是一个写成方阵的数字 ，这几节的核心是为了说明：矩阵其实就是一种向量变换（至于什么是变换下面会讲），并附带一种不用死记硬背的考虑矩阵向量乘法的方法
变换
【变换】本质上是【函数】（左）的一种花哨的说法，它接受输入内容，并输出对应结果，矩阵变换（右），同理，如下图
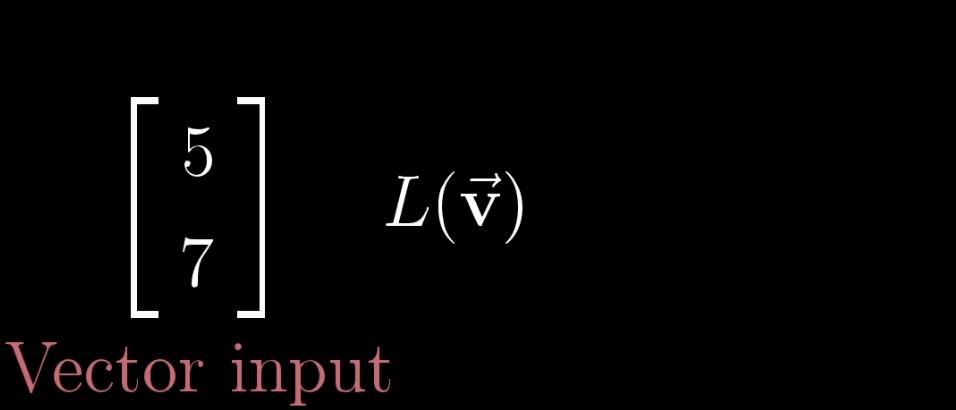
那既然两者意思相同，为何还要新发明一个词语装逼呢？其实不然，搞学术，不严谨就会出现纰漏。常说编程出现Bug，其实就是不严谨的一种体现，在写Code前，没有考虑到可能性的全集（虽然在一些大型程序中，考虑全集的做法有时候是没必要的，这是一对关于编程困难程度和不出的bug的博弈Trade-off），但是【变换】这个名词和不严谨其实没什么关系……
【变换】的表达方法暗示了我们可以用运动的方法来理解【向量的函数】这一概念，可以用可视化的方法来展现这组【变换】即输入-输出关系
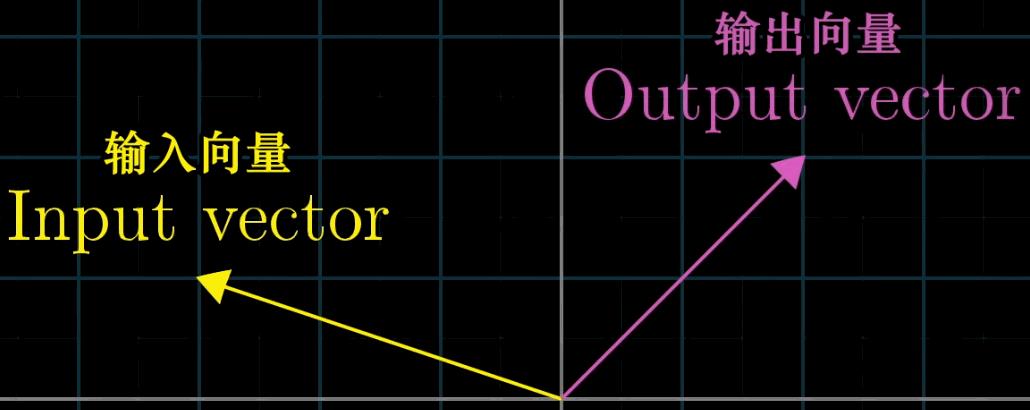
这世界上有非常多优美的变换，如果你将他们编程，并可视化，就能得到下图
线性变换
我们说具有以下两个性质的就是线性变换（直观可视化如下图）：
- 直线在变换后仍然保持为直线，不能有所弯曲
- 原点必须保持固定
一点扩展，如果保持保持直线但原点改变就称为：仿射变换（Affine Transformation）
一句话总结来说是：线性变换是“保持网格线平行且等距分布，并保持原点不动”的变换【重要】
如何用数值描述线性变换【核心】
这里需要使用上一节提到的工具，空间的基，也就是单位向量（基向量）： 和
任何的线性变换，你都可以通过对基向量
和
的变换，再对变换后的基向量
和
进行线性组合(
)得到。换句话说，对于任何的线性变换，你只需要关注两个基向量
例如， 变换到 (3,1) 的位置，
变换到(1,2) 的位置，并把
变换后坐标立起来作为方阵的第一列（绿色表示），
变换后的坐标立起来作为方阵的第二列（红色表示）。
构成了一个矩阵：，假设我们想要知道目标向量(−1,2)进行变换后的位置，那么这个矩阵就是对变换过程最好的描述，一动图胜千言
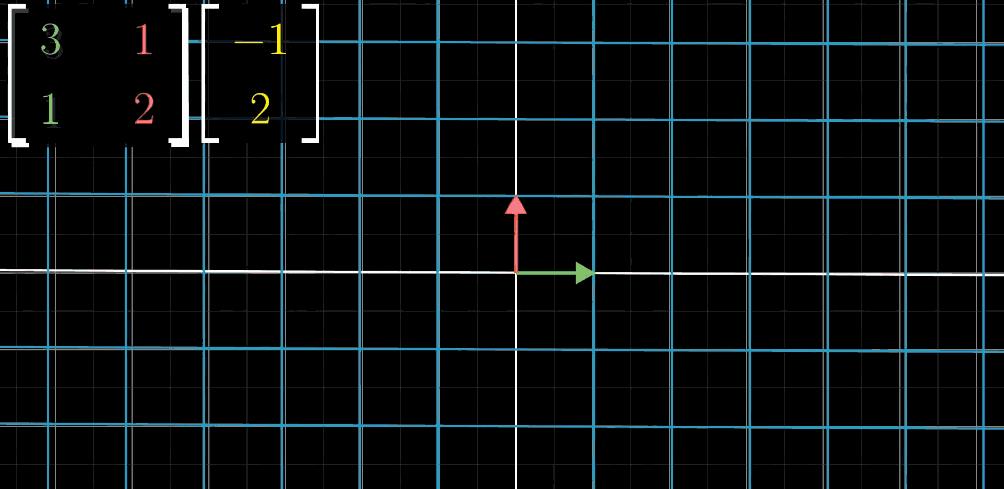
Step1：绿色 ^ıı^ （x轴）进行移动（变换）
Step2：红色 ^ȷȷ^ （y轴）进行移动（变换）
Step3：目标向量x轴坐标值与 ^ıı^ 变换后向量进行向量乘法
Step4：目标向量y轴坐标值与 ^ȷȷ^ 变换后向量进行向量乘法
Step5：两者进行向量加法，得到线性变换结果
更加一般的情况，我们用变量来代替其中的具体值：绿色代表 变换后的向量，红色代表
变换后的向量
上面的公式就是我们常说的矩阵乘法公式，现在，不要强行背诵，结合可视化的直观动图，你一辈子都不会忘记的
【线性】的严格定义
在给出一个数学化抽象的解释前，先做一下总结：
- 【线性变换】是操纵空间的一种手段，它保持网格线平行且等距分布，并保持原点不动
- 【矩阵】是描述这种变换的一组数字，或者说一种描述线性变换的语言
在数学上，【线性】的严格定义如下述公式，这些性质，会在之后进行讨论，也可以在这里就进行一些思考，为什么说向量加法和向量乘法贯穿线性代数始终，毕竟是线性代数，很重要的名词就是线性二字（“可加性”和“成比例”）
“可加性”
“成比例”
矩阵乘法与线性变换复合
据我的经验，如果丢掉矩阵的话，那些涉及矩阵的证明可以缩短一半 ——埃米尔·阿廷
It is my experience that proofs involving matrices can be shortened by 50% if one throws the matrices out -Emil Artin
复合变换
如果对一个向量先进行一次旋转变换，再进行一次剪切变换（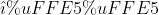 
保持不变第一列为（1,0）， 移动到坐标（1,1）） ，如下图所示
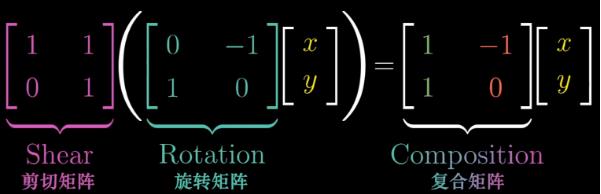
那么如果通过旋转矩阵和剪切矩阵来求得这个符合矩阵呢？为了解决这个问题，我们定义这个过程叫做矩阵的乘法
矩阵乘法
在这里我们发现，矩阵乘法的变换顺序是从右往左读的（这一个常识很重要，你得明白这一点，有基本概念），进一步联系和思考发现，和复合函数的形式，如 f(g(x)) ，是一致的
那么如何求解矩阵乘法呢？对线性代数有印象的同学你们现在能马上记起来那个稍显复杂的公式吗？如果有些忘记了，那么，现在，就有一个一辈子也忘不了的直观解释方法：
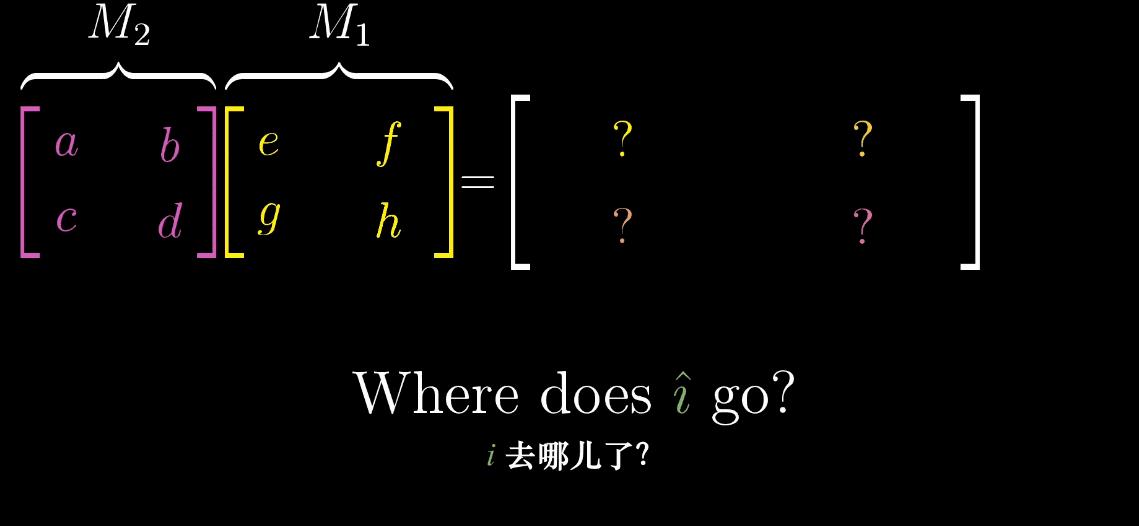
M1矩阵的第一列表示的是 变换的位置，先把它拿出来，
M2矩阵看成对这个变换过的 进行一次变换（按照同样的规则），就如上图所示。同理，针对
一样的操作过程，就可以得出这个表达式。这里我也不把它写出来了，按照这种思路，并且把上面的动图多看几遍，如果还能忘记，那就要去补一补基本的对几何图形的反应能力了（这也是一种能力，包括三维想象力，心算能力，都和记忆或肌肉一样，不锻炼，是不可能躺着被提高的）
另外两种常用来计算 矩阵乘法 的方法
我们这里只是在数值层面上面讨论这两种方法，当然这有悖于本篇文章的主题，毕竟我们通篇都是在讨论如何在几何层面理解矩阵和线性变换。所以我们这里也只是简单提及，并不做深入探究。
（1）矩阵乘法之行优先方法
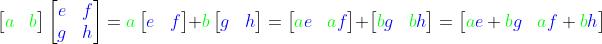
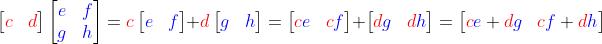
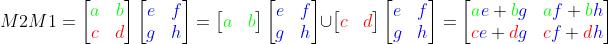
这种行优先的计算矩阵乘法的方法，在下面介绍并使用消元法求解线性方程组的解的时候非常有用，也更容易理解。
（2）矩阵乘法之元素值计算方法
通过上面行优先方法计算矩阵乘法的结果可知：最终计算得到的矩阵A，那么A的第i行第j列的元素的值，就是M1矩阵的第j列与M2矩阵的第i行的乘积，如下：
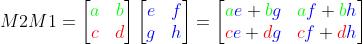
这种方法一般也被我们用来验证矩阵乘法的计算结果是否正确。
计算规则证明
有了上面的想法，可以自己尝试证明一下，矩阵乘法的交换律是否成立？矩阵乘法的结合律呢？你会发现，原来这么直观，根本不需要动笔算
三维空间
对三维空间内扩展的话，你会发现，显示生活中的每一种形态改变都能用一个 3*3 的矩阵来表示这个变换，这在机器人，自动化操作领域是非常重要的，因为你可以把现实生活很难描述的动作通过一个矩阵来表示，是一个连接数字和现实的重要桥梁和工具
n*n特殊矩阵(n阶方阵)
我们知道矩阵代表着一种线性变换，思考下面几个特殊n阶矩阵(这里只讨论n*n的方阵)是什么变换？
单位矩阵
在矩阵的乘法中，有一种矩阵起着特殊的作用，如同数的乘法中的1，这种矩阵被称为单位矩阵(一般记为)。它是个方阵，从左上角到右下角的对角线（称为主对角线）上的元素均为1。除此以外全都为0。
我们对向量应用矩阵乘法左乘单位矩阵
：
可以看出，向量在经过单位矩阵
变换之后，仍然得到其本身，换句话说，向量
在经过单位矩阵
变换之后并没有发生变化，所以我们称单位矩阵
所代表的变换为“恒等变换”。
对角矩阵
对角矩阵(diagonal matrix)是一个主对角线之外的元素皆为0的矩阵，常写为diag（a1，a2,...,an) 。对角矩阵可以认为是矩阵中最简单的一种，值得一提的是：对角线上的元素可以为 0 或其他值，对角线上元素相等的对角矩阵称为数量矩阵；对角线上元素全为1的对角矩阵称为单位矩阵。
单位矩阵：上面我们已经考虑了单位矩阵是对角矩阵的一种，其所代表的是一种“恒等变换”。
特殊的，对角矩阵中对角线上的元素全为0，所代表的零矩阵就是原点变换，它将任何向量都变换为0向量，也即任何向量变换之后都收缩到原点。
现在我们来考虑普通情况下的对角矩阵，也即对角线不全为1(单位矩阵)，也不全为0(零矩阵) 矩阵：
python与数据分析Numpy数值计算基础——补充