永磁同步电机模型之坐标变换

Posted 2022-10-16 海洋想想

文章目录

• 前言
• 旋转磁场
• clark变换和park变换
• • 坐标变换的目的
  • 坐标系
  • 3s/2s变换(clark变换)
  • 2s/2r变换(park变换)

前言

本文主要介绍永磁电机模型的坐标变化极其推导过程。本文主要参考资料：

• 哈肯.工业运动控制——电机选择、驱动器和控制器应用.机械工业出版社
• 永磁同步电机常见形式状态方程推导 传送门
• 陈伯时.自动控制系统——电力拖动控制.中央广播电视大学出版社
• 付兴贺，陈　锐.电机中AＢＣ 到ｄｑ０ 坐标变换的梳理与辨析

旋转磁场

在直流电机中，通过电刷与换向器切换转子的电流方向，让电机转子旋转起来。而在无刷电机或者永磁同步电机中，没有电刷或换向器，而转子通常为永磁体。这个时候需要在定子中通入正弦电流，从而形成旋转磁场，让永磁体在旋转磁场的推动下旋转起来。下面，重点介绍旋转磁场如何形成。

下图为永磁同步电机的结构示意图：

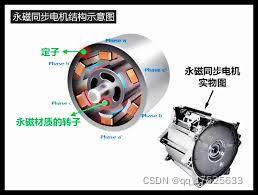
可以将定子模型简化为下图：

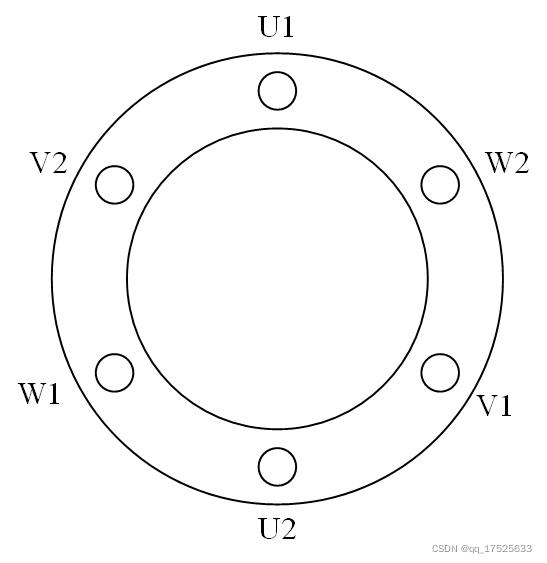
其中U1和U2，V1和V2，W1和W2形成三组空间位置相差120度的绕组。相同组的绕组内通入的电流相同，形成相同方向的磁场。
其抽象图如下图所示：

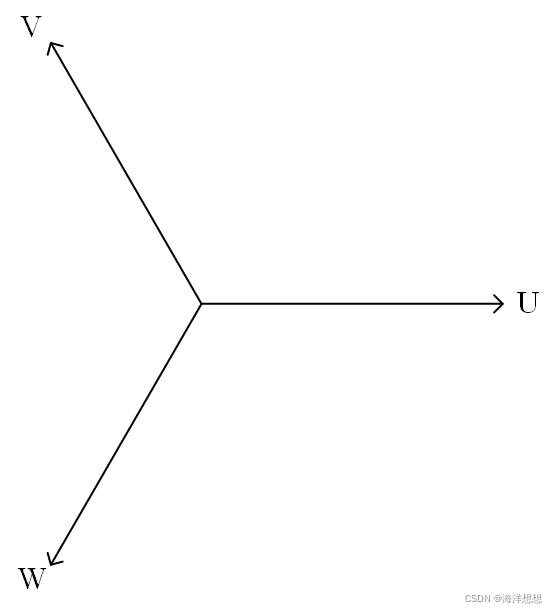
则分别在U，V，W通入三相交流电

$$\{\begin{array}{rl}& i_{\mathrm{U}}=I\mathrm{s}\mathrm{i}\mathrm{n}(\theta )\\ & i_{\mathrm{V}}=I\mathrm{s}\mathrm{i}\mathrm{n}(\theta +\frac{2\pi }{3})\\ & i_{\mathrm{W}}=I\mathrm{s}\mathrm{i}\mathrm{n}(\theta -\frac{2\pi }{3})\end{array}$$

如下图所示：

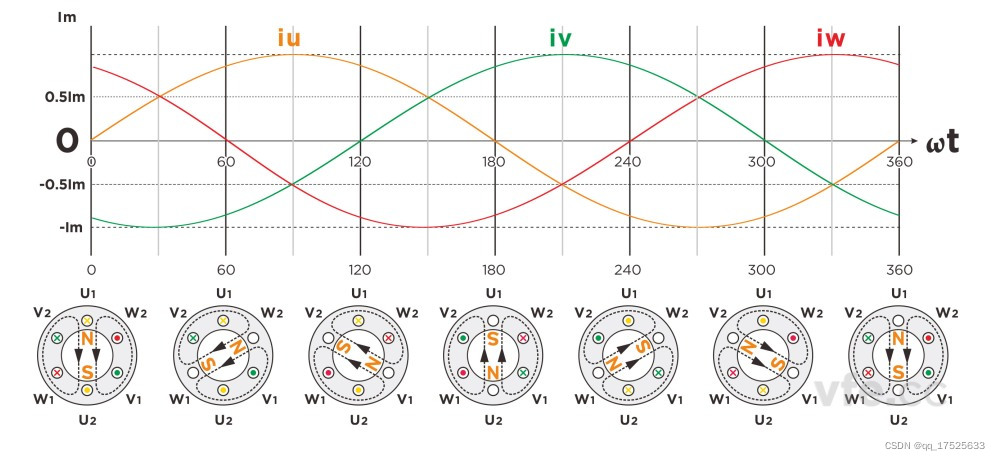
在每60度选取一点，可以发现，磁场确实随着电流变化而旋转。上图形象的展示了这一点。另外，也可以提供数学证明。

因为定子绕组是通过导线缠绕而成，可以将其视作电感， 根据公式：
$$\lambda =Li$$

其中，$\lambda$表示磁链，$L$为定子绕组电感，$i$为三项电流。

则可以知道，磁链与电流成正比，所以，可以将三相交流电产生的磁通用下式表示：

$$\{\begin{array}{rl}& {\lambda }_{\mathrm{U}}=LI\mathrm{s}\mathrm{i}\mathrm{n}(\theta )\\ & {\lambda }_{\mathrm{V}}=LI\mathrm{s}\mathrm{i}\mathrm{n}(\theta +\frac{2\pi }{3})\\ & {\lambda }_{\mathrm{W}}=LI\mathrm{s}\mathrm{i}\mathrm{n}(\theta -\frac{2\pi }{3})\end{array}$$

为了方便分析，可以建立下图($\alpha -\beta$坐标系)。因为$LI$为常数，可以设为$F_{\mathrm{m}\mathrm{a}\mathrm{x}}$ 。

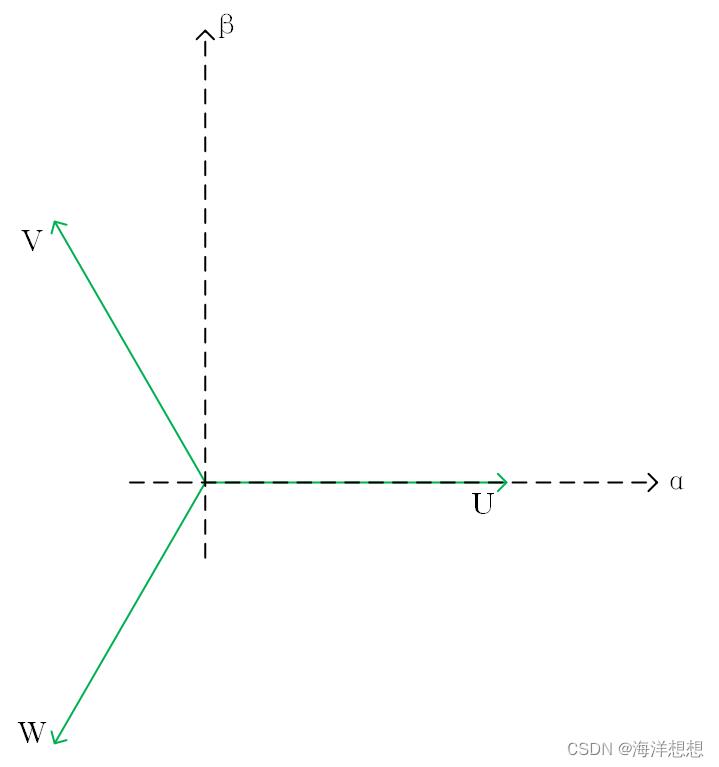
则可以得到三相叠加在$\alpha$轴的分量为：
$$\begin{array}{rl}{\lambda }_{\alpha }=& {\lambda }_{\mathrm{U}}\mathrm{c}\mathrm{o}\mathrm{s}0+{\lambda }_{\mathrm{V}}\mathrm{c}\mathrm{o}\mathrm{s}\left(\frac{2}{3}\pi \right)+{\lambda }_{\mathrm{W}}\mathrm{c}\mathrm{o}\mathrm{s}\left(-\frac{2}{3}\pi \right)\\ =& F_{\mathrm{m}\mathrm{a}\mathrm{x}}\mathrm{s}\mathrm{i}\mathrm{n}\theta +F_{\mathrm{m}\mathrm{a}\mathrm{x}}\mathrm{s}\mathrm{i}\mathrm{n}\left(\theta +\frac{2}{3}\pi \right)\mathrm{c}\mathrm{o}\mathrm{s}\left(\frac{2}{3}\pi \right)+F_{\mathrm{m}\mathrm{a}\mathrm{x}}\mathrm{s}\mathrm{i}\mathrm{n}\left(\theta -\frac{2}{3}\pi \right)\mathrm{c}\mathrm{o}\mathrm{s}\left(-\frac{2}{3}\pi \right)\\ =& F_{\mathrm{m}\mathrm{a}\mathrm{x}}\mathrm{s}\mathrm{i}\mathrm{n}\theta +\mathrm{c}\mathrm{o}\mathrm{s}\left(\frac{2}{3}\pi \right)\left[\mathrm{s}\mathrm{i}\mathrm{n}\left(\theta +\frac{2}{3}\pi \right)+\mathrm{s}\mathrm{i}\mathrm{n}\left(\theta -\frac{2}{3}\pi \right)\right]\end{array}$$

在$\beta$轴的分量为：
λ β = λ U s i n 0 +