机器学习回归决策树算法
Posted 赵广陆
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了机器学习回归决策树算法相关的知识,希望对你有一定的参考价值。
目录
1 原理概述
前面已经讲到,关于数据类型,我们主要可以把其分为两类,连续型数据和离散型数据。在面对不同数据时,决策树也可以分为两大类型:
- 分类决策树和回归决策树。
- 前者主要用于处理离散型数据,后者主要用于处理连续型数据。
不管是回归决策树还是分类决策树,都会存在两个核心问题:
- 如何选择划分点?
- 如何决定叶节点的输出值?
一个回归树对应着输入空间(即特征空间)的一个划分以及在划分单元上的输出值。分类树中,我们采用信息论中的方法,通过计算选择最佳划分点。
而在回归树中,采用的是启发式的方法。**假如我们有n个特征,每个特征有[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-qVtgkYjg-1664890813135)(https://tva1.sinaimg.cn/large/007S8ZIlly1gffer61u9zj307i024glh.jpg)]个取值,那我们遍历所有特征,尝试该特征所有取值,对空间进行划分,直到取到特征 j 的取值 s,使得损失函数最小,这样就得到了一个划分点。**描述该过程的公式如下:
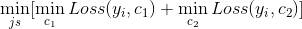
假设将输入空间划分为M个单元:R_1,R_2,…,R_mR1,R2,…,R**m 那么每个区域的输出值就是:c_m=avg(y_i|x_i\\in R_m)c**m=avg(y**i∣x**i∈R**m)也就是该区域内所有点y值的平均数。
举例:
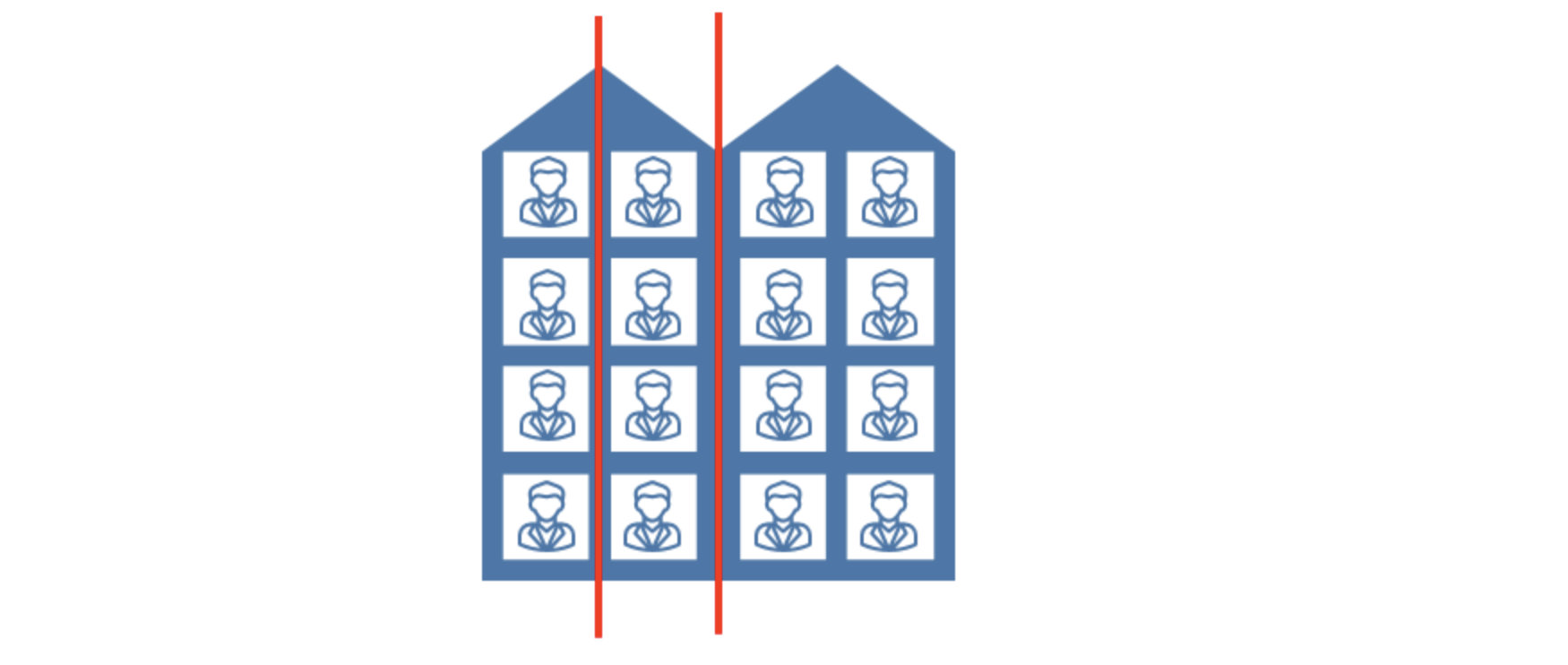
如下图,假如我们想要对楼内居民的年龄进行回归,将楼划分为3个区域R1,R2,R3(红线),
那么R1的输出就是第一列四个居民年龄的平均值,
R2的输出就是第二列四个居民年龄的平均值,
R3的输出就是第三、四列八个居民年龄的平均值。
2 算法描述
- 输入:训练数据集D:
- 输出:回归树f(x).
- 在训练数据集所在的输入空间中,递归的将每个区域划分为两个子区域并决定每个子区域上的输出值,构建二叉决策树:
- (1)选择最优切分特征j与切分点s,求解
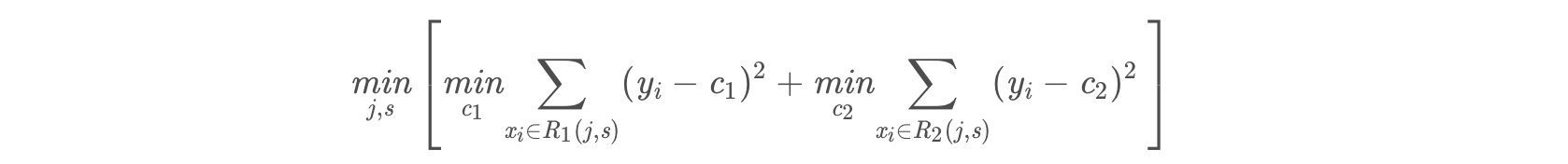 遍历特征j,对固定的切分特征j扫描切分点s,选择使得上式达到最小值的对 (j,s).
遍历特征j,对固定的切分特征j扫描切分点s,选择使得上式达到最小值的对 (j,s). - (2)用选定的对(j,s)划分区域并决定相应的输出值:
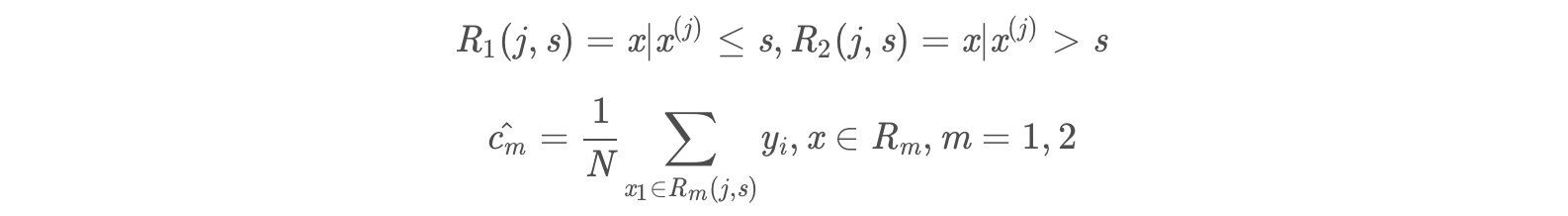
- (3)继续对两个子区域调用步骤(1)和(2),直至满足停止条件。
- (4)将输入空间划分为M个区域R1,R2,……,Rm, 生成决策树:
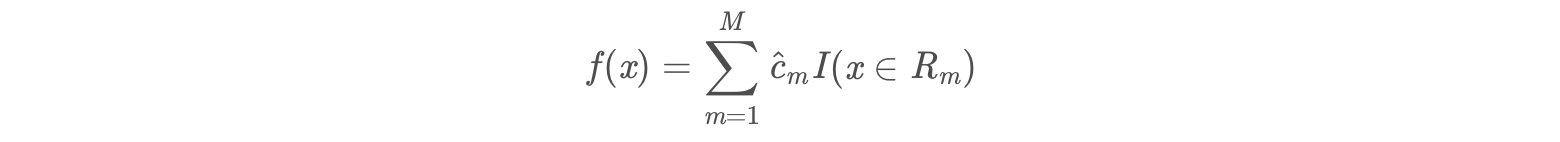
- (1)选择最优切分特征j与切分点s,求解
3 简单实例
为了易于理解,接下来通过一个简单实例加深对回归决策树的理解。
训练数据见下表,目标是得到一棵最小二乘回归树。
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| y | 5.56 | 5.7 | 5.91 | 6.4 | 6.8 | 7.05 | 8.9 | 8.7 | 9 | 9.05 |
3.1 实例计算过程
(1)选择最优的切分特征j与最优切分点s:
- 确定第一个问题:选择最优切分特征:
- 在本数据集中,只有一个特征,因此最优切分特征自然是x。
- 确定第二个问题:我们考虑9个切分点 [1.5,2.5,3.5,4.5,5.5,6.5,7.5,8.5,9.5] 。
- 损失函数定义为平方损失函数:Loss(y,f(x))=(f(x)-y)^2Los**s(y,f(x))=(f(x)−y)2
- 将上述9个切分点依此代入下面的公式,其中 c_m=avg(yi|xi\\in R_m)c**m=avg(y**i∣x**i∈R**m)
a、计算子区域输出值:
例如,取 s=1.5。此时R1=1,R2=2,3,4,5,6,7,8,9,10R1=1,R2=2,3,4,5,6,7,8,9,10,这两个区域的输出值分别为:
- c1=5.56c1=5.56
- c2=(5.7+5.91+6.4+6.8+7.05+8.9+8.7+9+9.05)/9=7.50c2=(5.7+5.91+6.4+6.8+7.05+8.9+8.7+9+9.05)/9=7.50
同理,得到其他各切分点的子区域输出值,如下表:
| s | 1.5 | 2.5 | 3.5 | 4.5 | 5.5 | 6.5 | 7.5 | 8.5 | 9.5 |
|---|---|---|---|---|---|---|---|---|---|
| c1 | 5.56 | 5.63 | 5.72 | 5.89 | 6.07 | 6.24 | 6.62 | 6.88 | 7.11 |
| c2 | 7.5 | 7.73 | 7.99 | 8.25 | 8.54 | 8.91 | 8.92 | 9.03 | 9.05 |
b、计算损失函数值,找到最优切分点:
把c1,c2的值代入到同平方损失函数:Loss(y,f(x))=(f(x)-y)^2Los**s(y,f(x))=(f(x)−y)2
当s=1.5时,
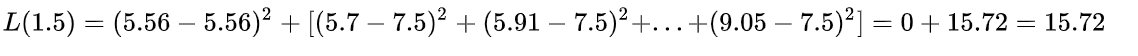
同理,计算得到其他各切分点的损失函数值,可获得下表:
| s | 1.5 | 2.5 | 3.5 | 4.5 | 5.5 | 6.5 | 7.5 | 8.5 | 9.5 |
|---|---|---|---|---|---|---|---|---|---|
| m(s) | 15.72 | 12.07 | 8.36 | 5.78 | 3.91 | 1.93 | 8.01 | 11.73 | 15.74 |
显然取 s=6.5时,m(s)最小。因此,第一个划分变量【j=x,s=6.5】
(2)用选定的(j,s)划分区域,并决定输出值;
- 两个区域分别是:R1=1,2,3,4,5,6,R2=7,8,9,10R1=1,2,3,4,5,6,R2=7,8,9,10
- 输出值c_m=avg(yi|xi\\in Rm),c1=6.24,c2=8.91c**m=avg(y**i∣x**i∈R**m),c1=6.24,c2=8.91
(3)调用步骤 (1)、(2),继续划分:
对R1继续进行划分:
| x | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| y | 5.56 | 5.7 | 5.91 | 6.4 | 6.8 | 7.05 |
取切分点[1.5,2.5,3.5,4.5,5.5],则各区域的输出值c如下表:
| s | 1.5 | 2.5 | 3.5 | 4.5 | 5.5 |
|---|---|---|---|---|---|
| c1 | 5.56 | 5.63 | 5.72 | 5.89 | 6.07 |
| c2 | 6.37 | 6.54 | 6.75 | 6.93 | 7.05 |
计算损失函数值m(s):
| s | 1.5 | 2.5 | 3.5 | 4.5 | 5.5 |
|---|---|---|---|---|---|
| m(s) | 1.3087 | 0.754 | 0.2771 | 0.4368 | 1.0644 |
s=3.5时,m(s)最小。
(4)生成回归树
假设在生成3个区域之后停止划分,那么最终生成的回归树形式如下:
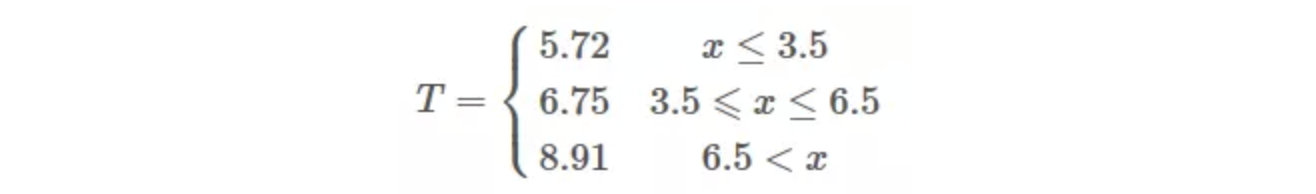
3.2 回归决策树和线性回归对比
import numpy as np
import matplotlib.pyplot as plt
from sklearn.tree import DecisionTreeRegressor
from sklearn import linear_model
# 生成数据
x = np.array(list(range(1, 11))).reshape(-1, 1)
y = np.array([5.56, 5.70, 5.91, 6.40, 6.80, 7.05, 8.90, 8.70, 9.00, 9.05])
# 训练模型
model1 = DecisionTreeRegressor(max_depth=1)
model2 = DecisionTreeRegressor(max_depth=3)
model3 = linear_model.LinearRegression()
model1.fit(x, y)
model2.fit(x, y)
model3.fit(x, y)
# 模型预测
X_test = np.arange(0.0, 10.0, 0.01).reshape(-1, 1) # 生成1000个数,用于预测模型
X_test.shape
y_1 = model1.predict(X_test)
y_2 = model2.predict(X_test)
y_3 = model3.predict(X_test)
# 结果可视化
plt.figure(figsize=(10, 6), dpi=100)
plt.scatter(x, y, label="data")
plt.plot(X_test, y_1,label="max_depth=1")
plt.plot(X_test, y_2, label="max_depth=3")
plt.plot(X_test, y_3, label='liner regression')
plt.xlabel("data")
plt.ylabel("target")
plt.title("Decision Tree Regression")
plt.legend()
plt.show()
结果展示
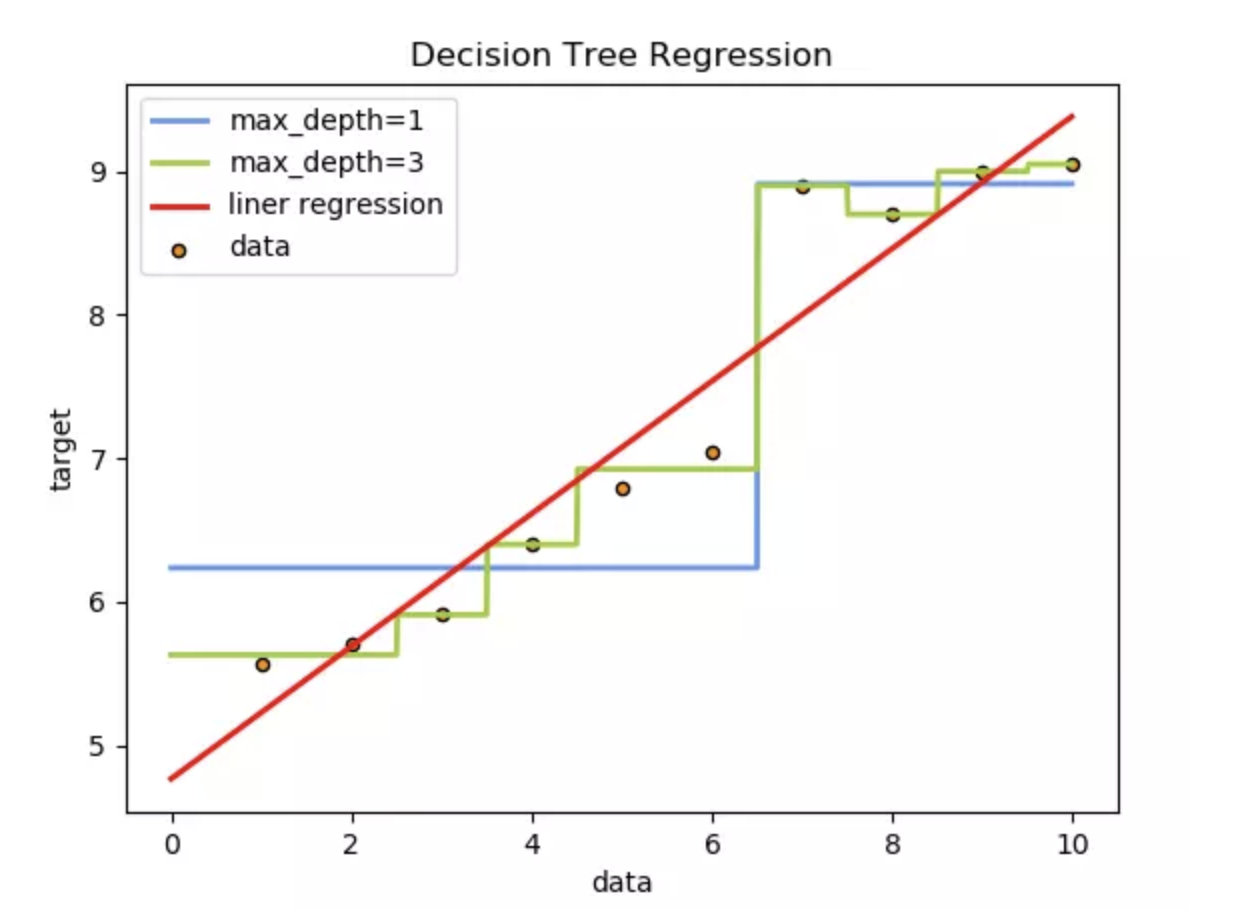
4 小结
-
回归决策树算法总结【指导】
-
输入:训练数据集D:
-
输出:回归树f(x).
-
流程:在训练数据集所在的输入空间中,递归的将每个区域划分为两个子区域并决定每个子区域上的输出值,构建二叉决策树
:
- (1)选择最优切分特征j与切分点s,求解[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-17DSdMof-1664890813141)(https://tva1.sinaimg.cn/large/006y8mN6gy1g8wecce1fpj31am04wwez.jpg)]遍历特征j,对固定的切分特征j扫描切分点s,选择使得上式达到最小值的对(j,s).
- (2)用选定的对(j,s)划分区域并决定相应的输出值:
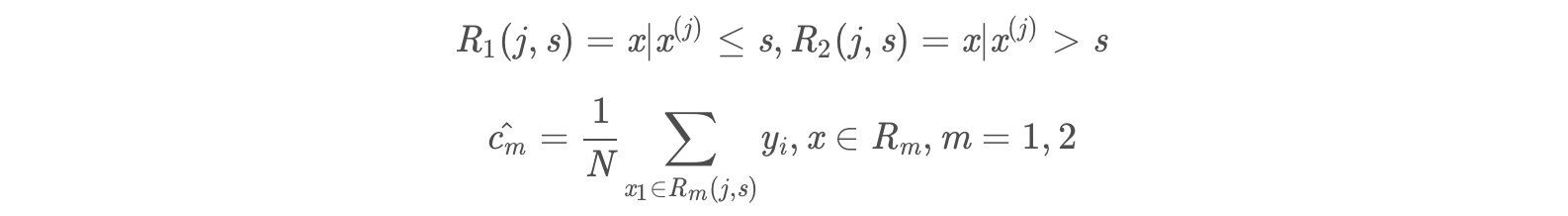
- (3)继续对两个子区域调用步骤(1)和(2),直至满足停止条件。
- (4)将输入空间划分为M个区域R1,R2,……,Rm, 生成决策树:
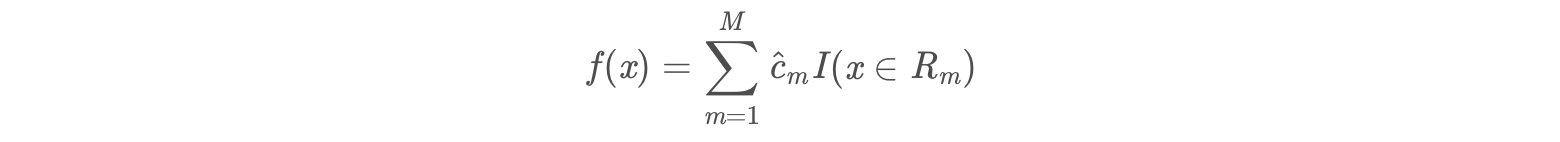
-
以上是关于机器学习回归决策树算法的主要内容,如果未能解决你的问题,请参考以下文章