第二节：半监督聚类之AP（Affinity Propagation）聚类（近邻传播聚类）

Posted 2022-09-26 快乐江湖

文章目录

• 一：基本思想
• 二：相关定义及术语
• • （1）相似度 Similarity
  • （2）相似度矩阵
  • （3）偏好参数 Preference
  • （4）吸引度和归属度
  • （5）阻尼系数 Damping factor
• 三：算法流程
• • （1）专业描述
  • （2）类比
• 四：SKlearn实现

一：基本思想

近邻传播聚类（Affinity Propagation Clustering, AP聚类）：基本思想是将全部数据点都当作潜在的聚类中心（exemplar），然后数据点亮亮之间连线构成一个网络（相似度矩阵），再通过网络中各条边的消息（responsibility和availability）传递计算出各样本的聚类中心

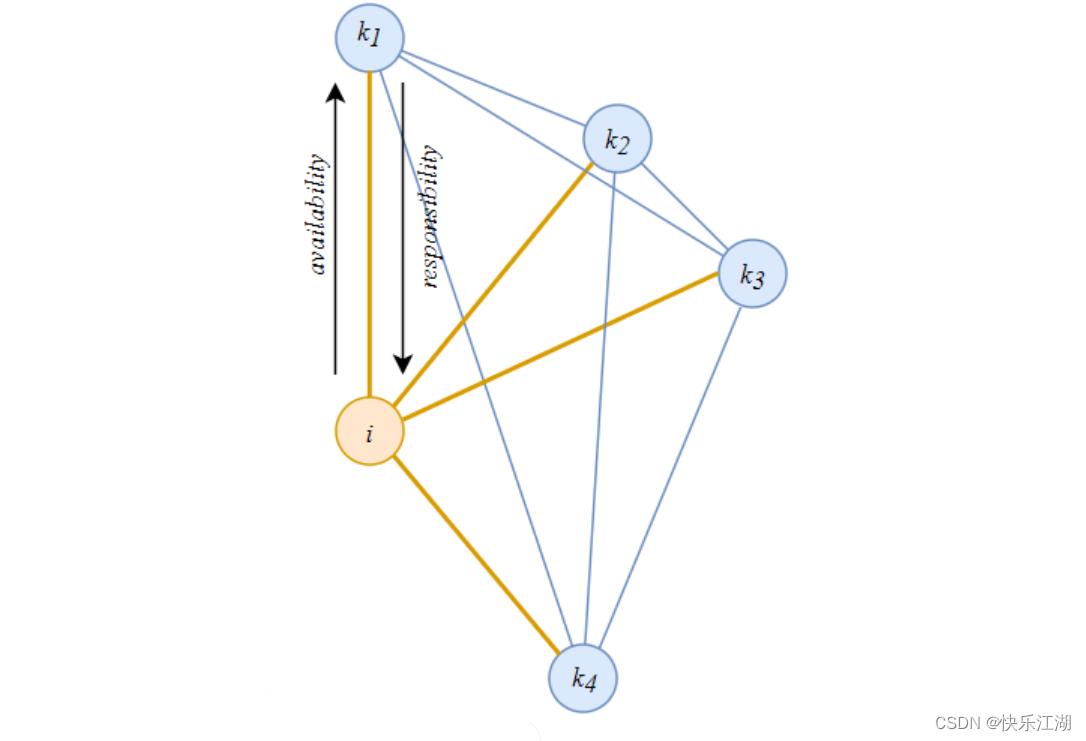
此过程中，共有如下两种消息在各节点之间传递

• 吸引度（responsibility）：对于$r(i,k)$而言，用于定量描述样本$k$作为样本$i$的聚类中心的程度
• 归属度（availability）：对于$a(i,k)$而言，用于定量描述样本$i$支持样本$k$作为其聚类中心的程度

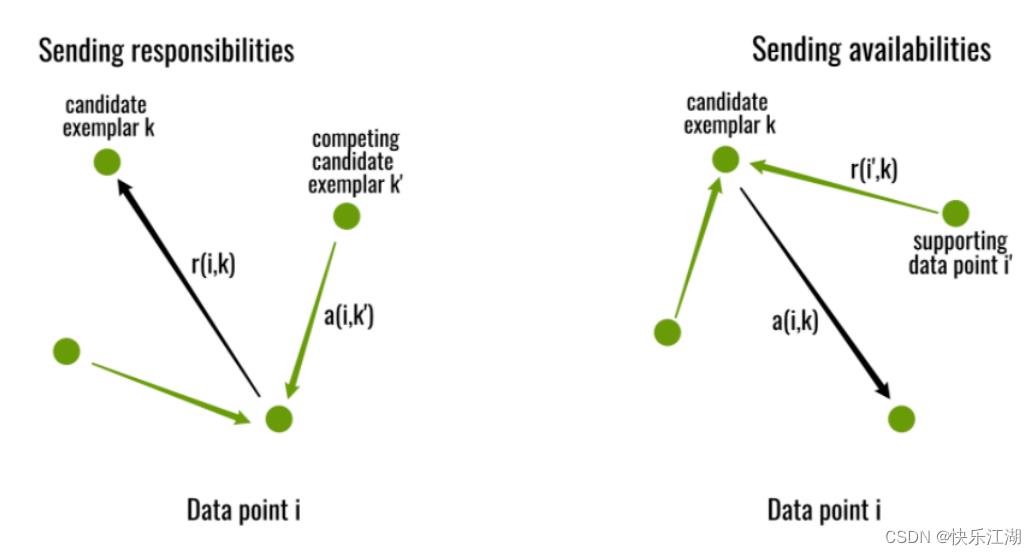
吸引度和归属度会分别形成吸引度矩阵和归属度的矩阵，然后算法会不断迭代更新两个矩阵

二：相关定义及术语

（1）相似度 Similarity

相似度（Similarity）：对于数据点$i$和$k$，使用$s(i,k)$描述两点之间的相似度，反映出了$j$作为$i$的聚类中心能力的大小，采用欧氏距离负值表示。$s(i,k)$值越大就表示$i$,$j$之间距离越近，也即$j$作为$i$的聚类中心的能力越强

$$s(i,k)=-||x_i-x_k|{|}^2$$

（2）相似度矩阵

相似度矩阵：作为算法的初始化矩阵，$n$个点就有由$n$×$n$个相似度组成的矩阵

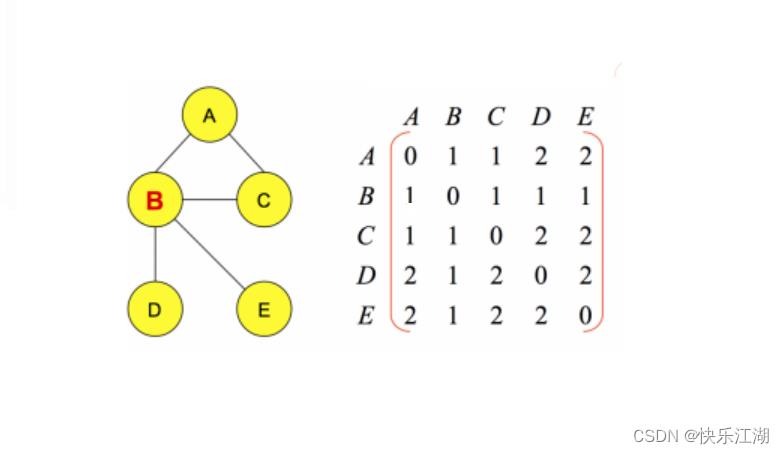
（3）偏好参数 Preference

偏好参数Preference：相似度矩阵中，主对角线上的值理论上为0，但是为了后续更好的应用相似度来更新吸引度和归属度，所以引入了该参数，用于定义相似度矩阵主对角线上的值。偏好参数越大说明各数据点成为聚类中心的能力越强，最终聚类中心的个数也就越多。偏好参数一般设置为相似度矩阵中所有值的最小值或中位数

（4）吸引度和归属度

吸引度（responsibility）：对于$(i,k)$而言，用于定量描述样本$k$作为样本$i$的聚类中心的程度

$$r(i,k)\leftarrow s(i,k)-\underset{k^{丶}s.t.k^{丶}\ne k}{\max }a(i,k^{丶})+s(i,k^{丶})$$

• $a(i,k^{丶})$表示除$k$外其他点对$i$的归属度，初始值为0
• $s(i,k^{丶})$表示除$k$外其他点对$i$的相似度
• $r(i,k)$值大于0，表示数据点$k$成为聚类中心的能力强。但是注意此时只考虑哪个点$k$成为点$i$的聚类中心可能性最大，但是没有考虑整个吸引度最大的$k$是否也经常成为其他点的聚类中心

归属度（availability）：对于$a(i,k)$而言，用于定量描述样本$i$支持样本$k$作为其聚类中心的程度

$$a(i,k)\leftarrow min0,r(k,k)+\sum _{i^{丶}s.t.i^{丶}\notin i,k}max0,r(i^{丶},k)$$

$$a(k,k)\leftarrow \sum _{i^{丶}\ne k}max(0,r(i^{丶},k)$$

• $r(i^{丶},k)$表示点$k$作为除$i$外其他点的聚类中心的相似度值，取所有大于等于0的吸引度值，加上$k$作为聚类中心的可能程度。即点$k$在这些吸引度值大于0的数据点的支持下，数据点$i$选择$k$作为其聚类中心的累积证明

$r(i,k)+a(i,k)$越大，则$k$点作为聚类中心的可能性就越大，并且$i$点隶属于以$k$点为聚类中心得的聚类可能性也就越大

（5）阻尼系数 Damping factor

阻尼系数 Damping factor：为防止数据振荡，引入阻尼系数，每个信息值等于前一次更新的信息值的$\lambda$倍加上此轮更新值的$1-\lambda$倍（$\lambda$位于0-1之间，默认为0.5）

三：算法流程

（1）专业描述

1. 给定数据集$D$
2. 计算相似度矩阵，并且设置偏好参数 Preference（这里设置为中值）
3. 计算吸引度矩阵$R$
4. 计算归属度矩阵$A$（注意开始计算时$R$和$A$需要进行初始化）
5. 迭代更新$R$和$A$，直至聚类中心在一定程度上不再更新或者达到最大的迭代次数
6. 根据得到的聚类中心，对数据进行聚类

（2）类比

近邻传播聚类算法中涉及的参数较多，尤其是在吸引度和归属度的计算公式，所以这里我们可以将该聚类算法比作一个选举过程进行理解

• 数据集中的所有点都会参加选举，它们既是选民也是参选人，聚类的目标是要选出几个人作为代表
• $s(i,k)$是指$i$对选$k$这个人有一个固定的偏好程度
• $r(i,k)$是指$k$在对$i$这个选民的竞争中的优势程度（用$s(i,k)$减去最强竞争者的评分）
• $r(i,k)$的更新过程就是选民$i$对各个参选人的挑选
• 从 a ( i , k ) ← m i n 0 , r ( k , k ) + ∑ i 丶 s . t . i 丶 ∉ i , k m a x 0 , r ( i 丶 , k ) a(i,k)\\leftarrow min\\0,r(k,k)+\\sum\\limits_i^丶s.t. i^丶\\notin\\i,k\\max\\0,r(i^丶,k)\\ a(i,k)←min0,r(k,k)+i丶以上是关于第二节：半监督聚类之AP（Affinity Propagation）聚类（近邻传播聚类）的主要内容，如果未能解决你的问题，请参考以下文章

  R语言Affinity Propagation+AP聚类实战

  均值漂移（MeanShift）谱聚类（Spectral clustering）AP聚类(Affinity propagation)聚类应用（客户分群）聚类应用（睡眠分析）

  Affinity Propagation+聚类

  Affinity Propagation+聚类

  数据挖掘聚类之k-means（转载）

  第一节：半监督聚类算法概述