第一节：半监督聚类算法概述

Posted 2022-09-12 快乐江湖

文章目录

• 一：半监督聚类
• 二：约束信息
• • （1）标签约束
  • （2）成对约束
  • • A：概述
    • B：举例

一：半监督聚类

半监督聚类（semi-supervised clustering）：传统的聚类学习任务是一种无监督学习任务，也即假设所有样本数据的簇标签未知。但是在某些学习任务中，用户具有某些领域的背景知识，也即约束信息。所以人们希望将这些领域知识应用到聚类任务中，所以这类学习任务称之为半监督聚类。半监督聚类可以分为：

• 广义的半监督聚类：在实际聚类任务中，相对于数据本身而言，数据的约束信息是更难以获取的，用户只能获取较为明显数据样本的标签，或只能得到施加在样本点之间的约束，所以这些信息称之为广义的半监督聚类
• 狭义的半监督聚类：它只限于针对样本点的约束信息

所以半监督聚类主要研究：如何利用少量的约束信息来得到更加准确的聚类结果，同时不仅利用约束样本提供的信息，而且考虑所有无约束样本集所隐含的结构信息

二：约束信息

约束信息：约束信息通常被认为是一种背景知识或领域知识，是分析数据时已知的信息。使用约束信息时，通常要对约束信息和无约束样本的关系做出一些假设，常见的有如下三种假设

• 簇性假设：是指数据倾向于形成分离的簇，并且同一簇中的数据有相同的簇标签
• 局部性假设：是指约束点与其近邻更有可能属于同一类别
• 流形假设：是指同一簇的数据位于一个低纬度流形上，这样聚类时就可以利用流形上的距离测度

根据约束存在方式的不同，约束信息分为如下两种

• 标签约束
• 成对约束

（1）标签约束

标签约束：在半监督聚类中，虽然整个学习任务是无监督的，但是有一部分数据的标签是可知的。标签约束就是指这种数据的已知标签，它可以看成是一种子集

利用标签约束的半监督聚类算法定义为：对于给定数据集$D$，标签约束集$L$，半监督聚类算法利用$L$中的信息将$D$中数据分配到对应的簇中

（2）成对约束

A：概述

成对约束：是一种指明两个实例的相对关系的约束信息；成对约束由以下两个集合构成

• 必连约束集（must-link set, ML）：对于两个数据点$x_i$和$x_j$，如果$(x_i,x_j)\in ML$，则数据点$x_i$和数据点$x_j$在实际中属于同一个簇，此时称$(x_i,x_j)$是一个必连约束（must-link）
• 勿连约束集（cannot-link set, CL）：对于两个数据点$x_i$和$x_j$，如果$(x_i,x_j)\in CL$，则数据点$x_i$和数据点$x_j$在实际中不属于同一个簇，此时称$(x_i,x_j)$是一个勿连约束（cannot-link）

利用成对约束的半监督聚类算法定义为：对于给定数据集$D$，必连约束集$ML$，勿连约束集$CL$，半监督算法的目标是通过最小化聚类的目标函数，利用$ML$和$CL$中的信息将$D$中数据分配到对应簇中

B：举例

下图给出了一个二维空间中数据的成对约束示例，包含两个簇，分别用圆点和三角形表示

• 必连约束集$ML=(x_3,x_4),(x_7,x_8)$使用实线连接
• 勿连约束集$CL=(x_1,x_2),(x_5,x_6)$使用虚线连接

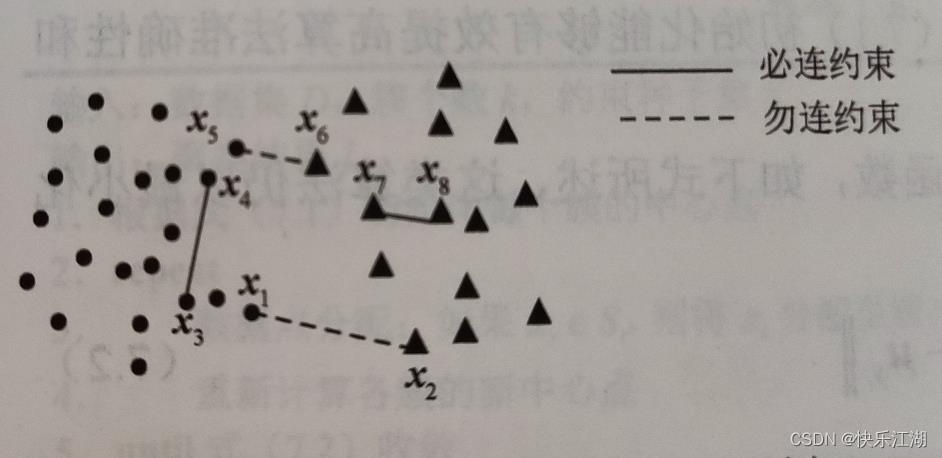
• 对于无监督聚类，不考虑以上的约束信息，由于$d(x_5,x_6)$ < $d(x_3,x_4)$，所以当$k=2$时，传统的$K-Means$方法可能会把$(x_4,x_5,x_6,x_7,x_8)$分到同一个簇中
• 对于半监督聚类，当拥有以上的约束信息后，一个有效利用成对约束的半监督聚类算法会将$(x_1,x_3,x_4,x_5)$分到同一个簇中

---

在很多实际问题中（例如图像检索、语音识别、GPS导航等等），往往难以获取数据的簇标签，但是用户可以指定两个实例是否属于同一簇。在给定标签约束的情况下，依然可以生成对应的必连约束和勿连约束

• 令簇标签相同的样本两两之间生成必连约束
• 令簇标签不同的样本两两之间生成勿连约束