PD控制基于matlab灰狼算法分数阶优化PD滑模控制器含Matlab源码 2006期

Posted 2022-08-08 海神之光

一、灰狼算法优化分数阶模糊控制器参数简介

1 分数阶模糊控制系统数学模型
分数阶控制系统的特征是微分方程，在动力系统或控制算法中，分数阶通常用微分或积分模型表示。

1.1 分数阶微积分
分数阶积分是对整数阶基本算子积分与微分的推广。微积分操作算子通常被定义为aDαt,将分数阶导数和分数阶积分定义为:

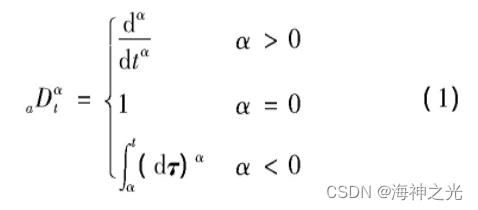
式中：a和t表示操作算子的上下限；α表示分数阶阶次且α∈R;τ表示切向单位向量。最常用的分数阶微积分定义是Riemann-Liouvile(RL)和Grunwald-Letnikou(GL)。分数阶微分阶α被定义如下：

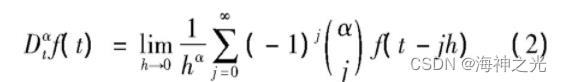
式中：Dαtf(t)表示分数阶导数。

在分数阶导数的数值计算中，α阶导数在kh(k=1,2,…)点，具体表示如下:

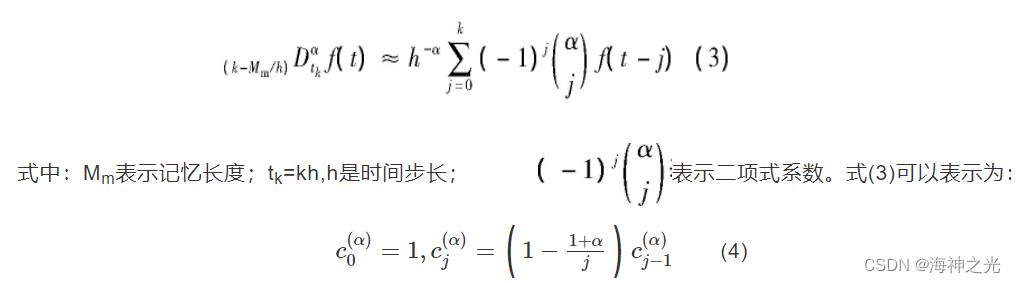
然后，分数阶差分方程的一般数值解被定义如下：

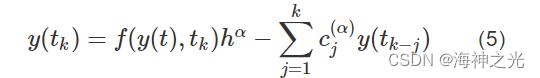
1.2 分数阶近似值算子
假设初始条件为零，分数算子在拉普拉斯域中定义为L(aDαtf(t))=sαF(s),其中sα为离散化微积分算子。Grunwald-Letnikov 近似值因其产生离散性质的等式值而被人们广泛使用。在这种方法下，离散化考虑以下模型：

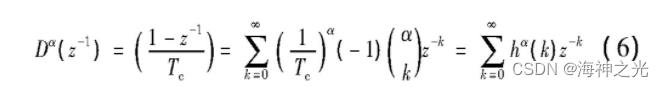
式中：hα(k)是脉冲序列；Tc表示采样频率。已经证明了有理式模型比多项式模型具有更快的收敛速度。因此采用Pade近似的方法，利用文中给出的定义，从脉冲响应中得到分数阶模型，具体模型表示为：

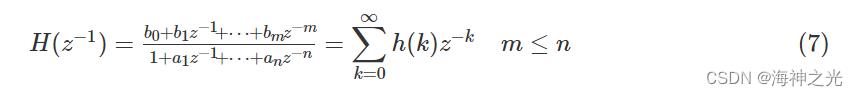
式中：m、n与参数ai、bi是通过调节hα(k)的系数m+n+1得到。

2 模糊控制器
模糊控制器是模拟专家的经验，并用语言形成严格的控制规则，然后通过控制规则控制其计算，实现目标任务。模糊控制器的一个重要的特性是将控制方案划分为多个区域。在每个区域，控制策略都可以通过使用一个规则来简单地建模，该规则将特定的操作按照所形成的区域关联起来。在所列出的文献中，尽管提出了几种模糊控制器模型配置，但是本文选取模糊分数阶PDα+I模型结构，因为此结构具有较好的稳定性与鲁棒性。

控制器配置如图1所示。其中：E、DE和IE分别代表误差、偏导误差和积分误差；e表示偏差值；v表示模糊输出量；Kp、Kd、Ki、Ku为增益值，前三项表示输入项，后一项为输出项。控制函数u是E、DE和IE的非线性映射函数，表示如下：

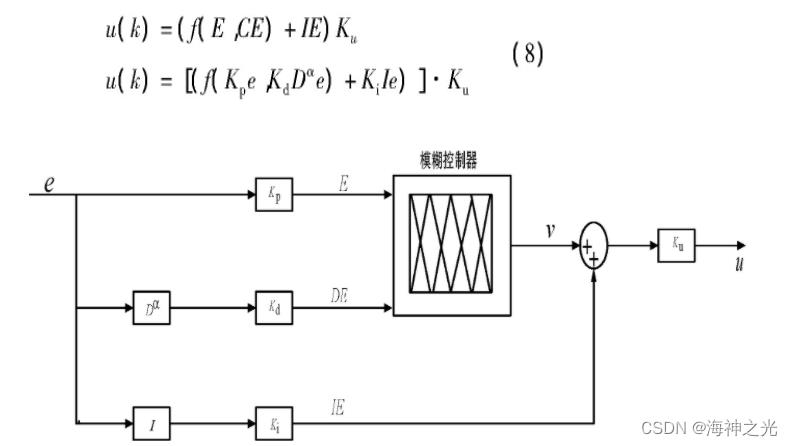
图1 模糊PDα+I控制器

3 GWO
灰狼优化算法是新型的群智能优化算法[14],该算法的灵感来源于灰狼群落的领导、指挥与狩猎行为。在该算法中，灰狼群被划分为四组，分别为α、β、δ、ω,前三种类型是作为领导阶层，ω是最底层灰狼种群，追随前3种种群。α、β、δ灰狼种群的更新公式如下：

D=|C·Xp(t)-X(t)| (9)
X(t+1)=Xp(t)-A·D (10)
A=2a·r1-a (11)
C=2·r2 (12)
式中：D表示灰狼与猎物之间的位置距离向量；t表示当前的迭代时间； A、C是向量系数；Xp是猎物的位置向量；X是灰狼的位置向量；a是步长因子，随着迭代次数的增加由2降到0;r1、r2取[0,1]间的均匀随机值。

在GWO中，认定α、β、δ为捕食猎物的最好的值，在优化的过程中，α、β、δ被认为是最好的解，其他灰狼为ω,不断更新位置朝向α、β、δ种群。根据以下数学模型，调整ω狼群的位置：
Dα=|C1·Xα-X| (13)
Dβ=|C2·Xβ-X| (14)
Dδ=|C3·Xδ-X| (15)
式中：Xα表示α灰狼的位置；Xβ表示β的位置；Xδ表示δ灰狼的位置；C1、C2、C3 是随机值；X表示当前解决方案位置。用式(13)、式(14)和式(15)分别计算当前解位置与α、β、δ灰狼位置之间的距离。定义距离之后，当前解的最终位置计算如下：
X1=Xα-A1·(Dα) (16)
X2=Xβ-A2·(Dβ) (17)
X3=Xδ-A3·(Dδ) (18)

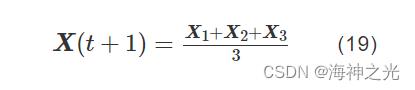
式(13)-式(15)定义了ω灰狼步长分别朝向α、β、δ灰狼位置。式(16)-式(19)定义了ω灰狼最终的位置。A、C这两个向量是随机值，能够有效平衡GWO勘探与开采能力。

Mirjalili 等[14]提出的GWO相比于其他著名的元启发式算法具有很高的性能。该算法具有很强的探测能力，而且能够避免局部最优。此外，较强的平衡勘探与开采能力能够有效解决一些复杂的工程问题。因此应用GWO优化模糊控制器参数问题。

4 用GWO对分数阶模糊控制器参数优化
在分数阶模糊控制系统的设计阶段，将参数计算过程转化为一个多维优化问题，将分数阶模糊控制器参数作为决策变量。在这种方法中，优化问题的复杂性往往产生多模态误差曲面，其代价函数往往难以最小化。提出一种分数阶模糊控制系统参数优化标定算法，采用GWO确定最优的参数值，如图2所示。

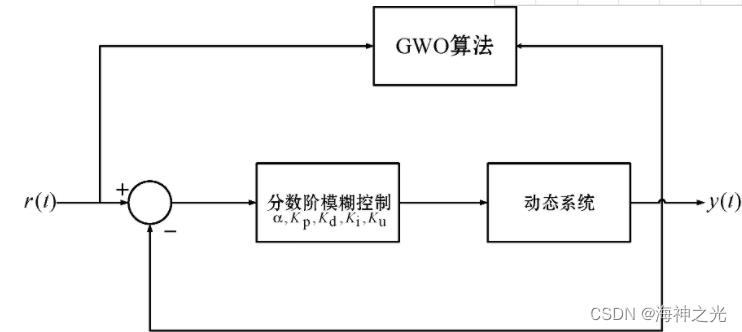
图2 基于GWO优化模糊控制器的参数问题
在GWO求解模糊控制器参数问题中，GWO中的最优解表示分数阶模糊控制器的一组最优的参数。分数模糊控制器参数(α,Kp,Kd,Ki,Ku)确定GWO候选解的维度。GWO的生物空间对应分数模糊控制器参数整定的解空间。另外，GWO的评价函数是分数模糊控制器的积分时间绝对误差(ITAE)[25]。ITAE指标J由以下模型定义：
J(α,Kp,Kd,Ki,Ku)=∫∞0t|r(t)-y(t)| (20)
式中：y(t)表示闭环阶跃响应函数；r(t)表示阶跃函数。
最小化目标函数为：
J(X) X=(α,Kp,Kd,Ki,Ku)∈R5 (21)

约束函数为：
0≤α≤3
0≤Kp≤5
0≤Kd≤5
0≤Ku≤5

控制器的参数值对控制器的性能具有较高的影响。例如，比例系数Kp值增加时，系统会变得敏感，响应速度更快，系统的稳态误差得以减小，从而使控制的精度提高。GWO优化的过程是通过连续计算ITAE值来评价该参数的质量，根据GWO的优化规则，通过连续迭代求出ITAE的最小值，从而得到一组分数阶模糊控制器的控制参数。

二、部分源代码

clear all
clc
close all
tic
%%Initilization
x0=[-pi pi 0 0 0 0];
Ts=[0 5]; %time span
%%Robot Specifications
L1=1; %link 1
L2=1; %link 2
M1=1; %mass 1
M2=1; %mass 2
% 
% 
% Ks=10;
% gama=9;
% alpha=4;
% beta=3;
% miu=1.5;
% % PID parameters for theta 1
% Kp1=38;
% Kd1=6;
% % PID parameters for theta 2
% Kp2=38;
% Kd2=6;

lb=[30 4 30 4 8 0 0 0 0];
ub=[51 12 51 12 20 14 8 5 3];
dim=9;

SearchAgents_no=5; % Number of search agents
Max_iteration=1; % Maximum numbef of iterations


[Best_score,Best_pos,GWO_cg_curve]=GWOr(SearchAgents_no,Max_iteration,lb,ub,dim);

Kpd=Best_pos
[T,X] = ode45(@(t,x) r2dof(t,x,Kpd),Ts,x0);



qd1=sin(4.17*T);
qdot_r1=4.17*cos(4.17*T);
qdot2_r1=-4.17*4.17*sin(4.17*T);
qd2=1.2*sin(5.11*T);
qdot_r2=1.2*5.11*cos(5.11*T);
qdot2_r2=-1.2*5.11*5.11*sin(5.11*T);
%%Output
th1=X(:,1); %theta1 wavwform
th2=X(:,2); %theta2 wavwform
th3=X(:,3);
th4=X(:,4);
th5=X(:,5);
th6=X(:,6);
%torque inputs computation from the 7th,8th states inside ODE
% F1=diff(X(:,5))./diff(T);
% F2=diff(X(:,6))./diff(T);
x1=L1.*sin(th1); % X1
y1=L1.*cos(th1); % Y1
x2=L1.*sin(th1)+L2.*sin(th1+th2); % X2
y2=L1.*cos(th1)+L2.*cos(th1+th2); % Y2


% Positions
GWO_cg_curve

toc

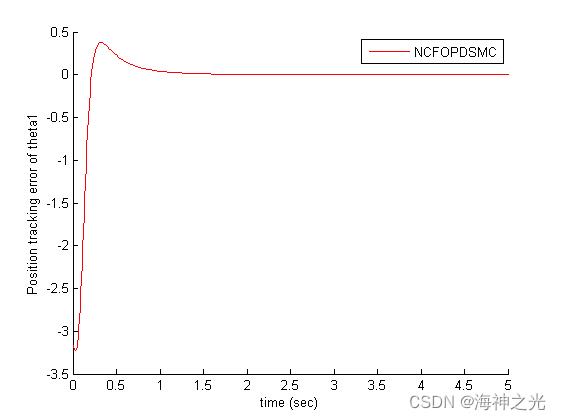
%theta1 error plot
figure(1)
hold on
plot(T,th1-qd1,'r')
legend('NCFOPDSMC')
ylabel('Position tracking error of theta1')
xlabel('time (sec)')
hold off

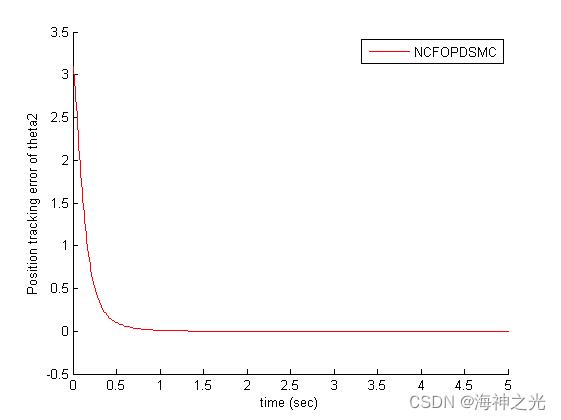
%theta2 error plot
figure(2)
hold on
plot(T,th2-qd2,'r')
legend('NCFOPDSMC')
ylabel('Position tracking error of theta2')
xlabel('time (sec)')
hold off

figure(3)
hold on
plot(T,th1,'r')
legend('qd1','FOPD','FSMC','NCFOPDSMC')
ylabel('Position tracking of theta1')
xlabel('time (sec)')
hold off

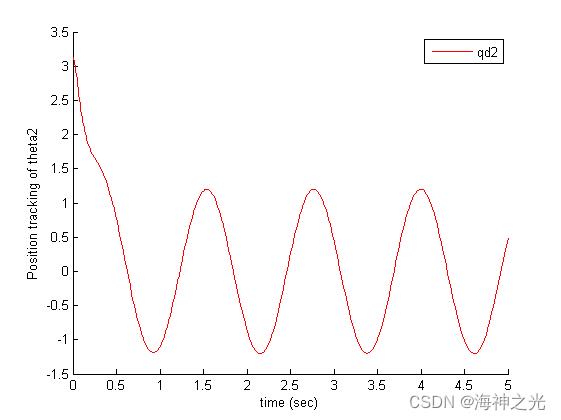
figure(4)
hold on
plot(T,th2,'r')
legend('qd2','FOPD','FSMC','NCFOPDSMC')
ylabel('Position tracking of theta2')
xlabel('time (sec)')
hold off

figure(5)
hold on
plot(T,th5,'r')
legend('FOPD','FSMC','NCFOPDSMC')
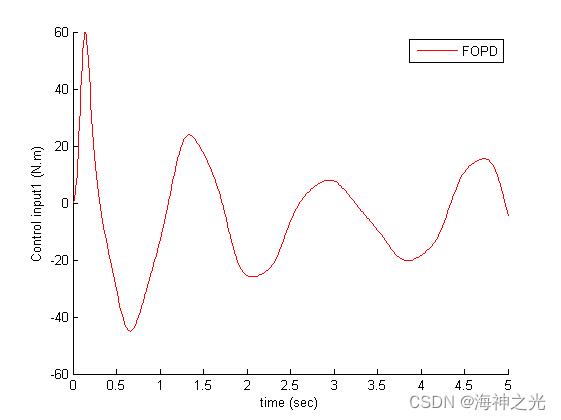
ylabel('Control input1 (N.m)')
xlabel('time (sec)')
hold off

figure(6)
hold on
plot(T,th6,'r')
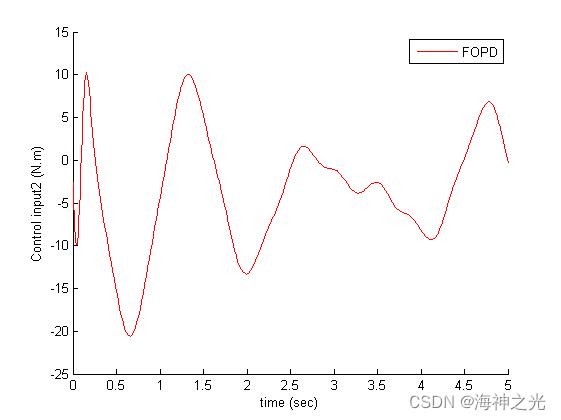
legend('FOPD','FSMC','NCFOPDSMC')
ylabel('Control input2 (N.m)')
xlabel('time (sec)')
hold off

figure(7)
hold on
plot(T,th3,'r')
legend('FOPD','FSMC','NCFOPDSMC')
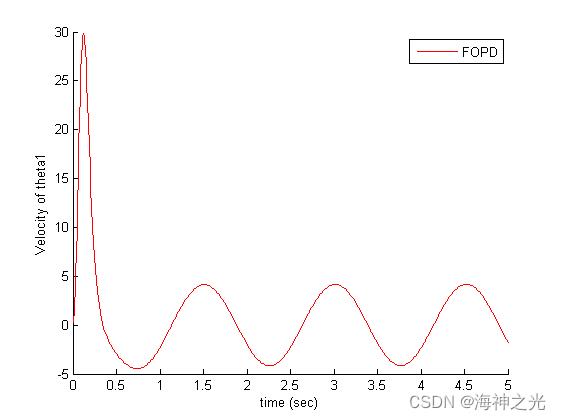
ylabel('Velocity of theta1')
xlabel('time (sec)')
hold off

figure(8)
hold on
plot(T,th4,'r')
legend('FOPD','FSMC','NCFOPDSMC')
ylabel('Velocity of theta2')
xlabel('time (sec)')
hold off

figure (9)
plot(GWO_cg_curve)
% close all
    

三、运行结果

四、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1] 范鲁娜.灰狼算法优化分数阶模糊控制器参数[J].计算机应用与软件. 2021,38(10)

3 备注
简介此部分摘自互联网，仅供参考，若侵权，联系删除