matlab改进灰狼算法求解路径优化

Posted 2021-12-20 张叔zhangshu

灰狼 优 化 算 法 ( grey wolf optimization algo-rithm，GWO)

是模仿灰狼等级划分和灰狼捕食行为而提出的群智能搜索算法。该算法具有控制参数少、收敛速度快和计算简单等优点，已在机器学习、函数寻优、数据挖掘、电力调度、控制器设计调优等方面得到广泛应用。目前应用灰狼优化算法求解 CVRP 的文献较少，因此本文提出一种基于 GWO 的农产品物流配送车辆路径优化方法。研究结果表明，与 PSO 和 GA 相比，在行驶里程和平均行驶成本方面，GWO 的成本最低且行驶里程最少。

GWO 算法

GWO 算法中，灰狼个体分为 α、β、δ 和 ω，其中，α 负责狼群的决策与管理; β 和 δ 为适应度次于 α 的灰狼个体; ω 为其他灰狼个体。GWO 算法主要包括包围、捕猎和攻击三种行为。1． 1 包围在整个算法过程中，首先灰狼包围猎物，

式( 1) 和式( 2) 中，| | 为绝对值符号; ·表示向量积; 珝D 为狼群和猎物之间的距离; 珗A = 2a·珒r1－ a，珗C = 2 ·珒r2; t 为当前迭代次数; 珗Xp为猎物所在位置; 珗X 为当前狼群所在位置; r1、r2为［0，1］之间的随机向量; a 为［2，0］之间的线性递减数。

1． 2 捕猎

包围猎物之后，狼群将捕猎猎物。假定 α、β、δ分别为全局最优解、全局第二解以及全局第三解，对 α、β、δ 重新定位:

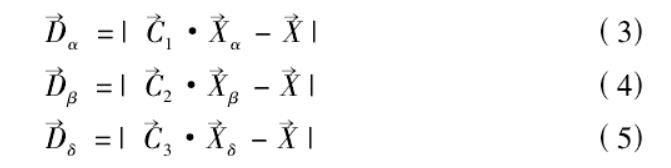
式( 3) ～ 式( 5) 中，珝Dα、珝Dα和 珝Dδ为 α、β、δ 与当前解 珗X 的近似距离; 珗Xα、珗Xβ、珗Xδ为 α、β、δ 的位置;珗C1、珗C2、珗C3为随机向量。当前解 珗X 和更新解 珗X( t +1) 为:

1． 3 攻击狼群

捕食的最后阶段就是攻击捕获猎物，攻击过程主要通过调节参数 a 实现。当 | A | ≤ 1 时，狼群将接近猎物( X*，Y*) 集中攻击猎物; 当| A |＞ 1 时，狼群将远离猎物

问题描述

农产品物流车辆路径优化可表述为［8 －9］: 假设农产品中心仓库，该中心仓库配备有 K 辆物流运输车，车辆载重容量为 qk( k = 1，2，3，…，K) ，配送需 求 点 有 L 个，第 i 个 需 求 点 的 需 求 量 为gi( max( gi) ≤ max( qi) ) ，完成需求点任务 i 农产品装载或卸货的时间为 Ti，其中任务 i 必须在时间段［ETi，LTi］内完成。ETi、LTi分别为任务 i 的最早开始时间和最迟开始时间。若农产品配送车辆早于 ETi到达需求点，则配送车辆等待; 否则，任务将被延迟。农产品物流车辆配

tic
clear
clc
%% 输入数据
dataset=importdata('input.txt');                    %数据中，每一列的含义分别为[序号，x坐标，y坐标]
x=dataset(:,2);                                     %x坐标
y=dataset(:,3);                                     %y坐标
vertexs=dataset(:,2:3);                             %提取各个城市的xy坐标
n=size(dataset,1);                                  %城市数目
m=2;                                                %旅行商数目
start=1;                                            %起点城市
h=pdist(vertexs);                                   %计算各个城市之间的距离，一共有1+2+......+(n-1)=n*(n-1)/2个
dist=squareform(h);                                 %将各个城市之间的距离转换为n行n列的距离矩阵
%% 灰狼算法参数设置
NIND=50;                                            %灰狼个体数目
MAXGEN=200;                                         %最大迭代次数
k=m;                                                %移除相邻路径的数目
%% 初始化种群
population=init_pop(NIND,n,m,start);
init_obj=obj_function(population,n,m,start,dist);   %初始种群目标函数值
%% 灰狼优化
gen=1;                                              %计数器
best_alpha=zeros(MAXGEN,n+m-1);                     %记录每次迭代过程中全局最优灰狼个体
best_obj=zeros(MAXGEN,1);                           %记录每次迭代过程中全局最优灰狼个体的目标函数值

alpha_individual=population(1,:);                   %初始灰狼α个体
alpha_obj=init_obj(1);                              %初始灰狼α的目标函数值
beta_individual=population(2,:);                    %初始灰狼β个体
beta_obj=init_obj(2);                               %初始灰狼β的目标函数值
delta_individual=population(3,:);                   %初始灰狼δ个体
delta_obj=init_obj(3);                              %初始灰狼δ的目标函数值
while gen<=MAXGEN
    obj=obj_function(population,n,m,start,dist);    %计算灰狼种群目标函数值
    %% 确定当前种群中的灰狼α个体、灰狼β个体和灰狼δ个体
    for i=1:NIND
        %更新灰狼α个体
        if obj(i,1)<alpha_obj 
            alpha_obj=obj(i,1); 
            alpha_individual=population(i,:);
        end
        %更新灰狼β个体
        if obj(i,1)>alpha_obj && obj(i,1)<beta_obj 
            beta_obj=obj(i,1); 
            beta_individual=population(i,:);
        end
        %更新灰狼δ个体
        if obj(i,1)>alpha_obj && obj(i,1)>beta_obj && obj(i,1)<delta_obj 
            delta_obj=obj(i,1); 
            delta_individual=population(i,:);
        end
    end
    %% 更新当前种群中灰狼个体的位置
    for i=1:NIND
        r=rand;
        individual=population(i,:);                 %第i个灰狼个体
        %概率更新灰狼个体位置
        if r<=1/3
            new_individual=cross(individual,alpha_individual,n);
        elseif r<=2/3
            new_individual=cross(individual,beta_individual,n);
        else
            new_individual=cross(individual,delta_individual,n);
        end
        population(i,:)=new_individual;             %更新第i个灰狼个体
    end
    %% 局部搜索操作
    [alpha_individual,alpha_obj]=LocalSearch(alpha_individual,n,m,k,start,dist);
    [beta_individual,beta_obj]=LocalSearch(beta_individual,n,m,k,start,dist);
    [delta_individual,delta_obj]=LocalSearch(delta_individual,n,m,k,start,dist);
    %% 记录全局最优灰狼个体
    best_alpha(gen,:)=alpha_individual;             %记录全局最优灰狼个体
    best_obj(gen,1)=alpha_obj;                      %记录全局最优灰狼个体的目标函数值
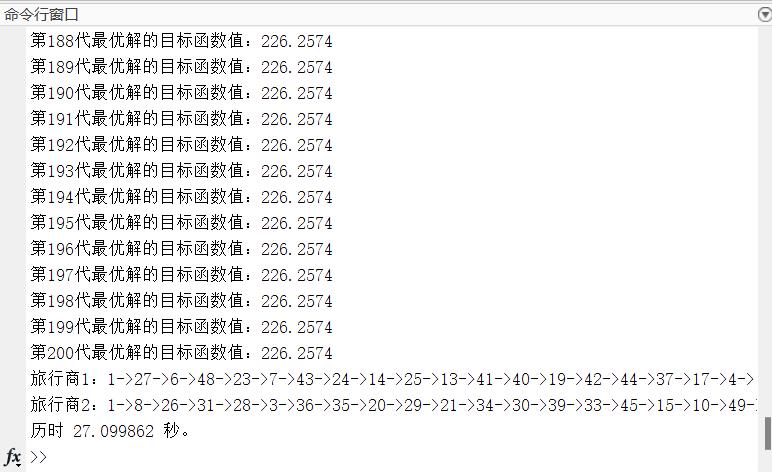
    %% 打印当前代数全局最优解
    disp(['第',num2str(gen),'代最优解的目标函数值：',num2str(alpha_obj)])
    %% 更新计数器
    gen=gen+1;                                      %计数器加1
end
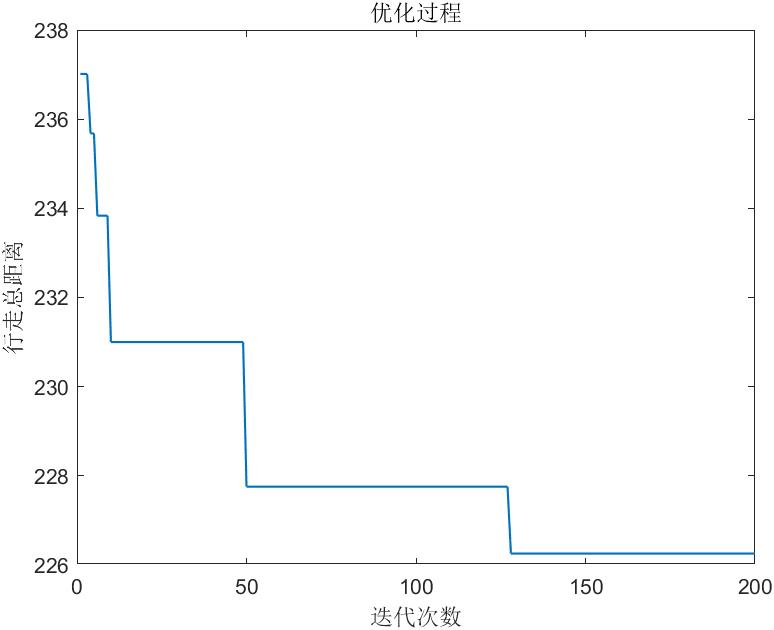
%% 打印每次迭代的全局最优灰狼个体的目标函数值变化趋势图
figure;
plot(best_obj,'LineWidth',1);
title('优化过程')
xlabel('迭代次数');
ylabel('行走总距离');
%% 将全局最优灰狼个体解码为旅行商行走路线方案
bestRP=decode(alpha_individual,n,m,start);          %将全局最优灰狼个体解码为旅行商行走方案
[bestTD,bestETD,bestMETD]=travel_distance(bestRP,dist);   %全局最优灰狼个体的目标函数值
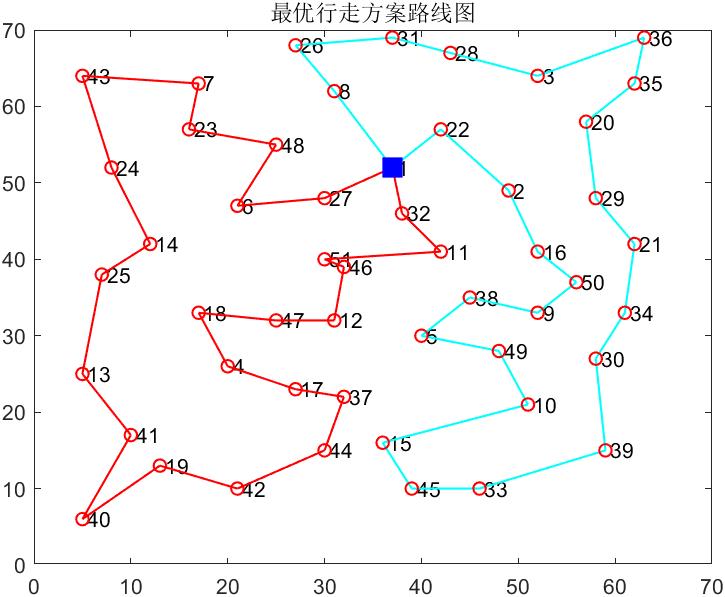
%% 画出最终行走路线图
draw_Best(bestRP,vertexs,start);
toc