声音信号处理基频检测和时频分析

Posted 2022-08-07 studyer_domi

1、内容简介

略
464-可以交流、咨询、答疑

2、内容说明

傅里叶变换建立了信号频谱的概念。所谓傅里叶分析即分析信号的频谱(频率构成)、频带宽度等。要想合成出一段音乐,就要了解该段音乐的基波频率、谐波构成等。因此,必须采用傅里叶变换这一工具。对于连续时间信号,其傅里叶变换为：

由于其变换两边的函数 和都是连续函数, 不适合于计算机处理。 MATLAB语言提供了符号函数FOURIER来实现傅里叶变换,但该函数需要信号的解析表达式。而工程应用中经常需要对抽样数据进行傅里叶分析,这种情况下往往无法得到信号的解析表达式,必须采用傅里叶变换的数值计算方法。

如果的主要取值区间为,定义为区间长度。在该区间内抽样N个点,抽样间隔为:

则有：

可以计算出任意频点的傅里叶变换值,假设的主要取值区间位于,要计算其间均匀抽样的k个值,则有：

其中，为频域抽样间隔。

基音周期检测也称为基频检测(Pitch Detection),它的目标是找出和声带振动频率完全一致的基音周期变化轨迹曲线,或者是尽量相吻合的轨迹曲线。基音周期检测在语音信号的各个处理领域中,如语音分析与合成、有调语音的辨意、低速率语音压缩编码、说话人识别等都是至关重要的,它的准确性及实时性对系统起着非常关键的作用,影响着整个系统的性能。 

浊音信号的周期称为基音周期,它是声带振动频率的倒数,基音周期的估计称为基音检测。基音检测是语音处理中的一项重要技术之一,它在有调语音的辨意、低速率语音编码、说话人识别等方面起着非常关键的作用;但在实现过程中, 由于声门激励波形不是一个完全的周期脉冲串,而且声道的影响很难去除、基音周期的定位困难、背景噪声的强烈影响等一系列因素,基音检测面临着很大的困难。而自相关基因检测算法是一种基于语音时域分析理论的较好的算法。

语音信号s(n)序列的短时平均幅度差函数定义为：

其中，w(m)是窗函数，尺是信号的平均值，因为语音信号的浊音段具有周性，假设基音周期为p，则在浊音段，在k=p，2p，3p…将出现谷点，谷点间的距离即为基音周期。

与短时自相关函数一样，对周期性的浊音语音，也呈现与浊音语音周期相一致的周期特性，不过不同的是在周期的各个整数倍点上具有谷值特性而不是峰值特性，因而通过的计算同样可以确定基音周期。而对于清音信号，却没有这种周期特性。利用的这种特性，可以判定一段语音是浊音还是清音，并估计 出浊音语音的基音周期。由于计算函数只需要加、减和取绝对值运算， 运算量较之短时自相关函数大大下降。同时，函数在基音周期点的谷 值比自相关函数的峰值更加尖锐，因此错判率相对较小，稳健性更高。但是当语音信号的幅度快速变化时，函数的谷值深度会减小，从而影响基音估计的精度。

时频分析相关理论介绍：

短时傅立叶变换（窗口傅立叶变换）是用一个很窄的窗函数取出信号，对其求傅立叶变换，假定信号在这个时窗内是平稳的，得到该时窗内的频率，并过滤掉了窗函数以外的信号频谱，确定频率在特定的时间内是存在的，然后沿着信号移动窗函数，得到信号频率随时间的变化关系，这样就得到了时频分布。可知，短时傅立叶变换的定义为：这种变换是线性的，而且满足叠加原理。换言之，如果是几个信号分量的线性组合，那么各个信号分量的时频线性组合可以得到的时频表示：线性由于不会产生交叉项干扰，所以是区分多分量信号的希望的性质，而且小波变换也是线性时频变换。傅立叶变换可以分别从信号的时域和频域观察信号 ，但却不能把二者联合起来描述信号。因为信号的时域中不包含任何频域信息；而频域中不包含时域信息。同时短时傅立叶变换概念直接，算法简单，已经成为研究非平稳信号十分有力的工具，在信号瞬时频率的估计领域得到了广泛的应用，并且是其它时频分析的基础。但是它存在两个问题：对窗函数的长度选择与窗函数的选择问题。为了得到更好的频域效果，因为窗函数的长度与频谱图的频率分辨率密切相关，因此信号的观察时间必须比较长。当信号变化很快时，反应频率与时间变化的关系将会受到影响；然而，当窗函数很短时，对于特定的窗函数来说，将会得到更好的效果。对比其他方法来说，短时傅立叶变换（STFT）虽然有着分辨率不高等明显缺陷，但由于其算法简单，实现容易，所以在很长一段时间里成为非平稳信号分析标准和有力的工具，而且不会产生多信号交叉干扰项，同时我们采用短时傅里叶变换算法估计瞬时频率对于频率分集和频率编码脉冲信号来说会更加方便。

语谱图是一种在语音分析以及语音合成中具有重要实用价值的时频图,它可以反映语音信号动态频谱特性,被视为语音信号的可视语言。其中语音信号是由发音器官的物理运动过程而产生的一种典型的非平稳信号。研究语谱图的主要理论方法就是傅立叶分析和短时傅里叶分析以及快速傅里叶变换。语音信号可以假定在10~30ms这样的短时间段内是平稳的,那么就可以应用稳态分析的方法来处理该段非平稳的音频信号。语谱图可以用二维的图谱来表示,即横坐标表示时间,纵坐标表示频率,时间和频率所对应的像素点的值表示能量值的大小,这种能量的大小是通过颜色来表示的,颜色深,表示该点的语音能量越强。具体可以概括为:首先根据原始音频信号长度来进行适当分帧,接着使用窗函数进行加窗处理,对加窗以后达到的每一帧音频信号进行快速傅里叶变换,根据傅里叶变换的系数计算相应时间和相应频率点上的信号能量,再将该能量进行分贝表示并且归一化,最后再对以上得到的数据矩阵进行伪彩色映射得到语音信号的语谱图。根据需要,可以得到二维灰度显示的语谱图、二维彩色显示的语谱图或者三维显示的语谱图。该方法同样适用于声乐信号的分析和处理。

二、乐理知识介绍：

乐音的基本特征可以用基波频率、谐波频谱和包络波形3个方面来描述。 基波频率：每个指定音调的唱名都对应固定的基波信号频率。所谓唱名是指平日读乐谱唱出的1(do)、2(re)、3(mi)、… ,每个唱名并未固定基波频率。当指定乐曲的音调时才知道此时唱名对应的频率值。如C调“ 1”的基波频率为261.63HZ,F调“1”的基波频率为349.23HZ,F调“ 5”的基波频率为523.25HZ。 谐波频谱:在音乐领域中称谐波为“泛音”,由谐波产生的作用称为音色变化。当指定音调之后,仅指定了乐音信号的基波频率,谐波情况并未说明。各种乐器,如钢琴或单簧管,都可以发出某一音调下的唱名,而人的听觉会明显感觉两者不同,这是由于谐波成分有所区别,频谱结构各异。包络波形:不同类型的乐器,包络形状也不相同。在音乐合成实验中,为简化编程描述,通常把复杂的包络函数用少量直线近似。于是,乐音波形的包络呈拆线。有时为了保证在乐音的邻接处信号幅度为零,也可以用指数衰减的包络来表示,这也是最简单的办法。

3、仿真分析

 

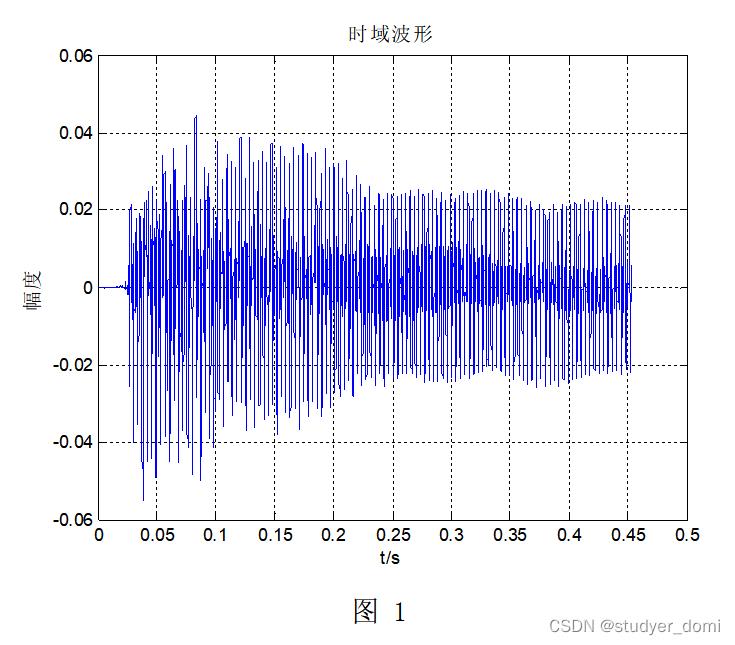
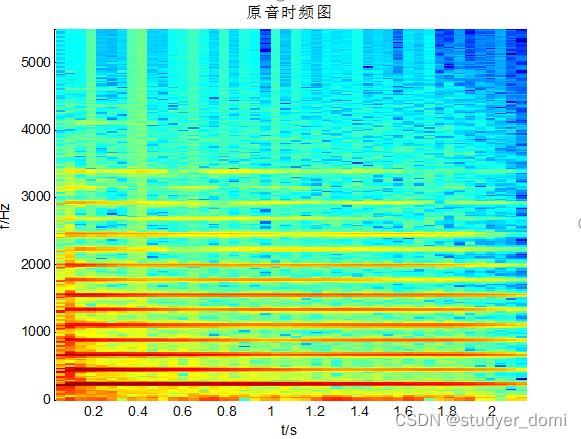
4、参考论文

略