实时音频编解码之四 LPC和LSF

Posted 2022-05-18 shichaog

​
本文谢绝任何形式转载，谢谢。
1.5.1 基频

语音信号的基频（pitch）通常用$F0$或$F_0$表示，基频是物理意义上的概念，人耳听到的基频称为基音，基音反应的是人耳对基频的感知。对于低比特率的编码器，基频的准确性对于合成的语音质量是至关重要的，基频反映的是准静态语音信号的周期性，这一周期性和声带的震动频率相关，基频是声带短时平均震动次数，由于基频是由人的器官发声形成而不是器件的震动产生，因此存在显著的变动，工程上将周期变动和幅度的变用抖动（jitter）和振幅微扰（shimmer）表示，基频取决于人的声带和声道生理结构，婴儿的基频在500Hz左右，儿童在250~400 Hz ，女性在120Hz~500Hz（周期为2ms~8ms），男性在50Hz~250Hz（周期为4ms~20ms），男人的基频比女人和小孩的要低些，对于个体而言$F0$​取决于声道的长度，这和一个人的身高也是有关系的。基频滞后（称为pitch lag，是按采样点计数的延迟值）是基频周期的一种表示方式，可以通过信号自相关最大值确定基频滞后，为了防止基频跳动，通常需要对信号进行预处理，且对基频进行跟踪和平滑处理过滤跳跃值，大部分基频跟踪算法先用带通滤波器滤波和高频分量预处理，然后再利用短时相关性进行基频估计，最后在进行数学意义上的平滑后处理。听觉上F1对人耳的影响比F0大，图1-15显示了基频及其谐波关系，频谱包络对于参数编码器至关重要。

图1-15 基频及其谐波关系

基频通常逐帧计算，由于声道共振峰、语音段起始难以确定以及噪声和回声等使得准确基频估计较为困难，工程实现中基频估计需要在计算复杂度和性能平衡，很多算法用于估计基频周期，其中最为常用的算法是自相关方法，且自相关有如Levsion递归等快速算法。
设x[n]为采集到的语音信号，n是采样点索引，设帧长为N，某帧结束索引为m，则自相关值为：
$$r_{xx}[l,m]=\sum _{n=m-N+1}^{m}x[n]x[n-l]$$
上式反应了帧$x[n],n=m-N+1,...,m$和时移信号$x[n-l]$之间的相似性，基频滞后值通常在基频存在的可能范围内搜索（如8kHz采样率时，基频范围54.4Hz~400Hz，周期2.5ms~18.3ms，而滞后值$l$在20~147），选择自相关最大的$l$为滞后值，这一滞后值（20~147）可以用7比特编码，因为147-20=127可以用$2^7=128$表示。在计算自相关之前，通常需要进行低通滤波以去掉高频成份和带外噪声的干扰。

1.4.2 全零点和全极点滤波

M阶全极点滤波器的传递函数是：
$$H(z)=\frac{1}{A(z)}=\frac{1}{1+\sum _{i=1}^M{a}_i{z}^{-i}}$$
当输入信号是$x[n]$，输出信号是$y[n]$时，时域响应如下：
$$y[n]=x[n]-\sum _{i=1}^M{a}_{i}y[n-i]$$
其表达形式和IIR滤波器一致。

M阶全零点滤波器的传递函数是：
$$A(z)=1+\sum _{i=1}^M{a}_i{z}^{-i}$$
类似的，当输入信号是$x[n]$，输出信号是$y[n]$时，时域响应如下：
$$y[n]=x[n]+\sum _{i=1}^M{a}_{i}x[n-i]$$
其表达形式和FIR滤波器一致。

上述全零点和全极点滤波器的传递函数存在互逆的关系，
$a_i$是滤波器的系数。上述两式称为滤波器的直接型实现方式，还有格型实现方式，在格型实现方式中会引入反射系数。反射系数方法可以直接从系数值监督滤波器的稳定性，格型滤波实现可以不用求解系数$a_i$也增加了滤波的稳定性，基于建模的语音编码方式根据语音生成的特点，采用较为简单的全零点模型对声道进行建模。
1.4.3 LPC

精确重构短时功率谱包络对于音质和清晰度是非常重要的，谱峰对于感知质量更为关键，而LPC参数的包络谱（反应了短时内的共振峰信息）更有益于谱峰的表示，对于低比特率语音编码器，LPC广泛用于谱包络编码，语音编码中LPC是逐帧获取的，通常50帧/秒，LPC通常10~20阶，为压缩比特率通常会对LPC进行量化压缩，由于LPC系数是逐帧获取的，因而有两种方式对齐进行量化，分别是标量量化和矢量量化，标量量化是逐点量化，点与点之间是独立的，而矢量量化是对每帧提取的一组LPC系数量化，其目标是最小化各组失真，这使得矢量量化在各量化比特率下失真都比标量量化小。
语音的相关性有短时和长时两种，短时相关性的滞后小于2ms，而长时相关滞后时间通常大于2ms，这是因为长时相关性基于语音信号的周期性特征，短时相关性确定了功率谱包络，长时相关性确定了功率谱的精细结构，这里的LPC系数是由短时相关性获取的，短时相关性是声道形状的函数。

语音是连续信号，如下图所示，短时采样点之间是相关的，

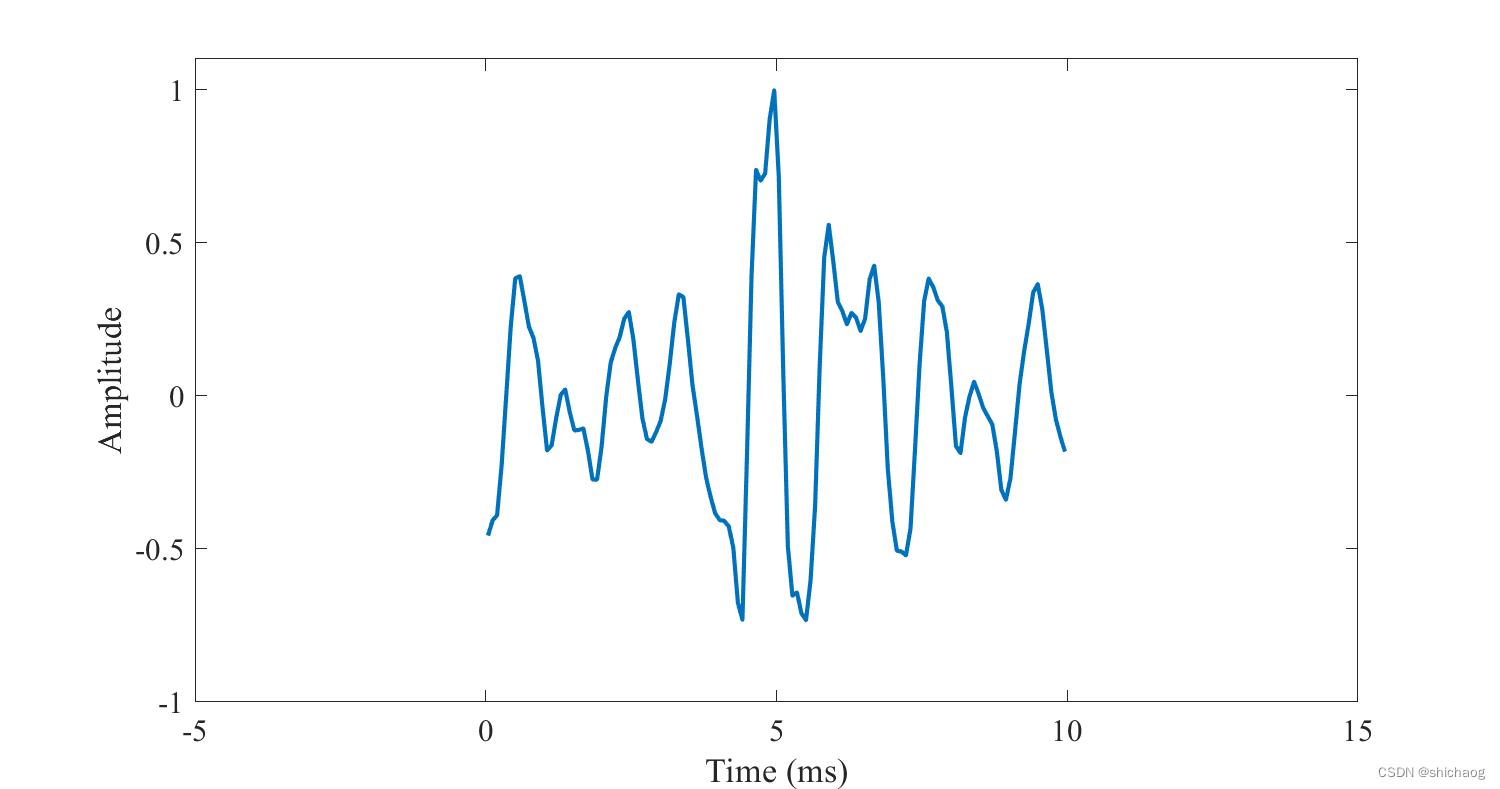
根据这一相关性，由前一个采样点$x[n-1]$可以预估当前采样点$\hat{x}[n]$，当前点的真实值可以用下式计算：
$$x[n]\approx \hat{x}[n]=x[n-1]$$
使用越多（对于语音多达50个左右）的历史采样点真实值，估计当前点真实的有效信息越多，准确性越高，可以用p个点估计当前点的值：
$$\hat{x}[n]=-\sum _{k=1}^P{a}_k^{(P)}x[n-k]$$
这是一个标准的线性预测器，是自回归模型，预测器的误差（预测残差）定义为：
$$e[n]=x[n]-\hat{x}[n]=x[n]+\sum _{k=1}^P{a}_k^{(P)}x[n-k]=\sum _{k=0}^P{a}_k^{(P)}x[n-k],a_0=1$$

线性预测器的P个系数（因符合自回归滤波模型，故这里P也称为阶数，即LPC系数的阶数），$a_1,a_2,\cdots ,a_p$是LPC系数，P值通常是10~20，$e[n]$被称为残差信号，由于两个相关信号相减之后的残差信号自身相关性很弱，因而残差信号谱包络是近乎平坦的，将残差信号用Z域表示为：
$$E[z]=A[z]S[z]$$
其中 A [