文献翻译阅读-NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis

Posted 2023-03-29 Super__B

目录

• 信息
• 简介
• 相关工作
• • 神经3D表示
  • 视角合成和基于图像的渲染
• 方法
• • 体渲染技术（用离散形式表示连续积分）
  • 优化神经场的技术
  • • 位置编码
    • 分层体积抽样
    • 实施细节
• 结果
• 结论
• 参考

信息

NeRF，即Neural Radiance Fields（神经辐射场）的缩写。研究员来自UCB、Google和UCSD。

Title：NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis

Paper：https://arxiv.org/pdf/2003.08934.pdf

Code：https://github.com/bmild/nerf

简介

通过优化底层场景提出了一种新视角合成的方法，这种算法采用的是全连接的神经网络来映射场景向量，其中输入是连续的5D表示(位置信息$(x,y,z)$+视角方向($\theta ,\varphi$))，输出是体积密度$\sigma$+该空间位置的视角相关的辐射(可以理解为color)。沿着相机光线查询5D表示来合成视图（使用经典的体渲染技术），该技术可微所以要求输入是一系列的已知相机姿势的照片。
前驱知识介绍：

• 体积密度$\sigma$：不透明度即射线通过点$(x,y,z)$累计的辐射量；
• 全程使用神经网络全连接，并未使用卷积层，用的是MLP(多层感知机)去学习神经辐射场这个函数；
• 位置编码：使得MLP可表达更高频函数-解决了分辨率低问题；
• 分层抽样：解决对高频场景需充分采样问题。
• 整体步骤：
  • 使用相机光线穿过场景采样一系列3D点；
  • 使用这些点和其相关的2D视角方向作为NN的输入产生$\sigma$和颜色；
  • 使用体渲染技术将$\sigma$和颜色生成对应的2D图像；
  • 用真实图像和生成图像做均方误差优化参数。
    收集上半球面的3D图像输入，即可生成各种位姿的新视角的2D图像

nerf优势

• 将具有复杂连续场景的表示为5D神经辐射场的方法，参数化为基本的MLP网络；
• 可微的体渲染技术优化标准的RGB图像值，分层抽样策略使得MLP的容量分配给可见场景内容的空间；
• 位置编码升维输入的5D坐标使得nerf可以表征更高频的场景内容。

相关工作

神经3D表示

优化坐标映射到距离函数/占用域的深度网络，但是在真实3D场景表现很弱比如ShapeNet；之后通过可微分的渲染函数放宽了真实3D形状的要求，可以允许只用2D图像来优化；Sitzmann的工作是用不直接的神经3D表示输出特征向量和RGB值在每一个3D坐标，提出了一种由递归神经网络组成的可微分渲染函数，该网络沿着每条射线行进以确定曲面的位置。
尽管这些方法已经可以有效表达复杂场景建模，但是还限制于几何复杂度低的简单形状，导致渲染出来的图像过于平滑。

视角合成和基于图像的渲染

密集视图采样：可以通过简单的采样插值重建逼真的视图
稀疏视图采样：计算机视觉和图像社区已经有重大进展
现有的方法：

1. mesh-based 表示方法-局部最小值问题，并且需要固定网格在优化之前，在不受约束的真实场景不可用；
2. 体渲染：输入一堆RGB图像，既适合复杂场景又能可微优化。早期是用观察的图像直接可体素网格上色，近期是使用多场景大型数据集训练NN再预测采样的体积表示，再用alpha合成或者沿射线合成渲染新的视图。但是由于离散采样，时间和可见复杂度较差，根本限制了缩放到更高分辨率图像的能力。—文章在全连接的网络参数内编码连续体积来规避该问题（更高质量并且存储成本低）。

方法

整体训练框架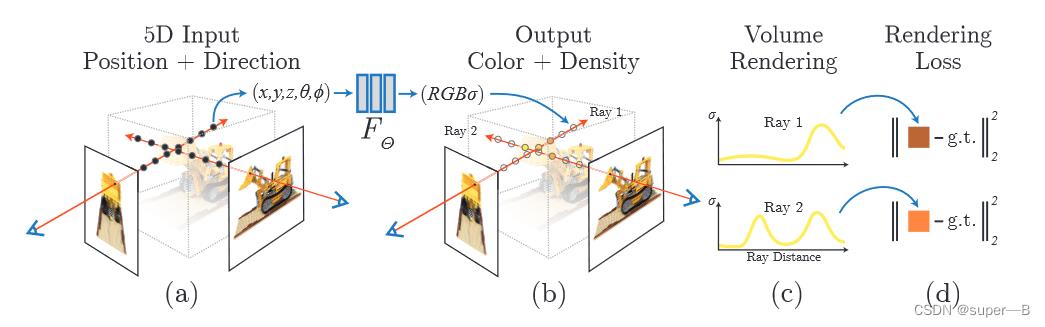
1.沿相机射线采样5D坐标($x,y,z,\theta ,\varphi$)，其中视角用三维笛卡尔坐标$d$表示；
2. 将位置信息给MLP生成对应的($r,g,b,\sigma$)；
3. 使用体渲染技术将($r,g,b,\sigma$)合成图像；
4. 体渲染函数可微，最小化合成图像和真实观测图像的残差来优化。

细节：$\sigma$只用位置信息$x$预测，($r,g,b$)用位置信息$x$和$d$预测—MLP先用8层全连接(使用RELU激活函数、每层256个通道)，使得输入$x$后输出$\sigma$+一个256维的特征向量$vector$；该$vector$再和相机射线方向$d$作为输入送入另一个全连接层(RELU+128通道)，输出视角相关的RGB值。

体渲染技术（用离散形式表示连续积分）

参数说明：

• $\sigma (x)$—射线在$x$处终止的概率即不透明度；
• $r(t)=o+td$—射线$r$的方向；
• $C(r)$—射线$r$在时间起点到时间终点的预测颜色值；
• $T(t)$—沿$t_n$到$t$的射线累计透射率（即射线从$t_n$到$t$不撞击任何粒子的概率）可以理解为光线射到这“还剩多少光”；
• $\sigma (t)$—表示不透明度；
• ${\delta }_i=t_{i+1}-t_i$—是相邻样本的距离；

积分形式：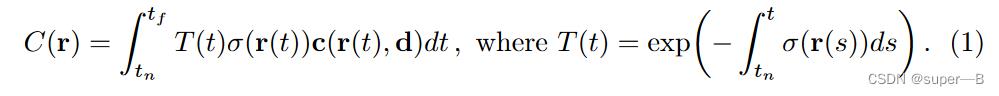
公式也说明密度只与位置信息有关；颜色与位置信息和观测方向都有关系。
如何沿着射线对空间中的颜色进行积分？

1. 一个点的密度越高，射线通过它之后变得越弱，密度和透光度呈反比；
2. 一个点的密度越高，这点在这个射线下的颜色反应在像素上的权重越大；

分层抽样:把$[t_n,t_f]$均匀N等分，然后每个小区间随机抽一个样本$t_i$离散形式：

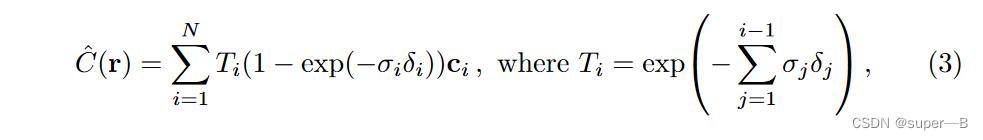注意：原来的积分权重是$T(t)\sigma (r(t))$，离散的形式是$T_i(1-exp(-{\sigma }_i{\delta }_i))$，而$1-exp(-{\sigma }_i{\delta }_i)$是和密度${\sigma }_i$呈正比的。

优化神经场的技术

位置编码

问题：尽管MLP可以无限逼近真实函数，但是在颜色和几何图像的高频变化下依然存在表现很差，如红圈图像部分直接模糊—由Rahaman的工作知深度神经网络倾向于学习低频部分。
解决方案：将输入先用高频函数映射到更高维可见，可以更好拟合包含高频变化的数据。所以把神经网络函数由两个函数组成：$F_{\Theta }=F_{\Theta }^{{}^{\prime }}\circ {\rm Y}$。
其中$F_{\Theta }^{{}^{\prime }}$是常规的MLP函数，${\rm Y}$是一个映射函数-实现高维编码器作用。
${\rm Y}(\cdot )$作用于每一个分量：$(x,y,z)$和$d$，并且归一化到$[-1,1]$，在文章中$L$值对于${\rm Y}(x)$取10（相当于原来的3维增加了7维），对于${\rm Y}(d)$取4。

分层体积抽样

问题：对渲染图像没有贡献的自由空间和遮挡区域仍然被重复采样+空间的密度分布不均匀，如果射线均匀随机采样的话，渲染效率会比较低。并且从上面分析可知道，整个渲染过程就是对射线的采样点颜色进行加权求和，其中权重是$w_i$。
解决方案：用两个网络表示场景：“粗”+“细”
对渲染公式中的颜色权重$w_i$作为对应区间采样的概率，我们训练两个辐射场网络，一个粗糙网络（Coares）一个精细网络（Fine）。粗糙网络是在均匀采样得到比较少($N_c$)的点进行渲染并训练的网络，用来对输出$w_i$进行采样概率估计。—重写了离散函数形式如下所示：

再将结果归一化：${\hat{w}}_i=w_i/\sum _{j=1}^{N_c}{w}_j$，以${\hat{w}}_i$为概率分布采样$N_f$个点，用$N_c$

论文泛读NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis

NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis | NeRF: 用于视图合成的神经辐射场的场景表示 | 2020年

出自文献：Mildenhall B, Srinivasan P P, Tancik M, et al. Nerf: Representing scenes as neural radiance fields for view synthesis[C]//European Conference on Computer Vision. Springer, Cham, 2020: 405-421.

Fig. 1：通过场景的一些图片作为输入，我们提出一种优化连续的 5D 神经辐射场表示的方法

摘要

• 我们提出一种方法，使用较少的视图（view）作为输入，对一个连续、隐含的体积场景函数（volumetric scene function）进行优化，从而实现了关于复杂场景的新视图合成的最先进的结果。
• 我们的算法用全连接深度网络来表示场景，其输入是 5D 坐标：空间位置$(x,y,z)$ 和视角方向（viewing direction）$ (θ,ϕ)$；其输出是体积密度（volume density）和该空间位置上发射出来的辐射亮度（radiance，与视角相关）。
• 通过沿着相机光线（camera rays）获取 5D 坐标，使用经典的立体渲染（volume rendering）技术，我们将输出的颜色和密度投影到图像上，从而实现视图合成。
• 由于立体渲染是可导的，神经网络的优化，只需要提供一系列确定相机位姿的图像。

1 介绍

• 我们的工作，用新的方法解决了在

  视图合成（view synthesis）

  中长期以来的问题。

  • 我们直接优化一个连续的 5D 场景表示（scene representation）的参数（网络权重），根据捕获到图像，最小化渲染误差。
  • 我们把静态场景表示为连续的 5D 函数（指输入是 5D ），输出在各个空间点 $(x,y,z)$ 和各个方向 $(\theta ,\varphi )$ 发射出来的辐射亮度和密度（就像可导的透明度，控制穿过 $(x,y,z)$ 的射线，可以累加多少辐射亮度）。
  • 我们的方法是优化一个深度全连接的神经网络，没有用到卷积层，全连接神经网络又称多层感知器（MLP）；我们用这个 MLP 来表示这样的函数：根据一个 5D 坐标 $(x,y,z,\theta ,\varphi )$，回归输出一个体积密度和视角相关的 RGB 颜色。

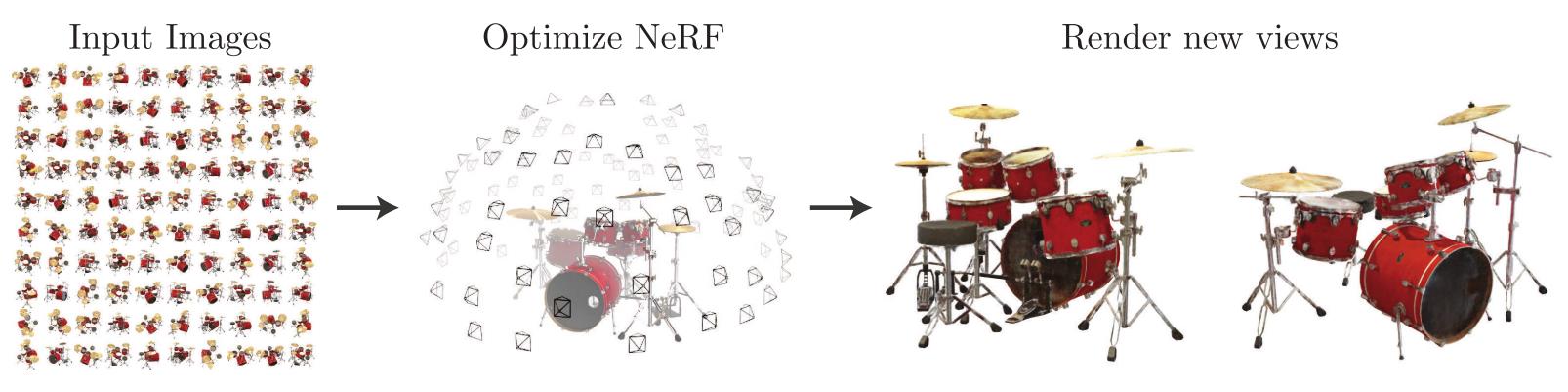
• 整个流水线如下图所示：

Fig. 2: 神经辐射场场景表示 和 可导的渲染流程 的概述。我们的图像合成，通过（图 a）沿着相机光线采样出 5D 坐标（位置和视角方向）；（图 b）把位置喂给 MLP，生成颜色和体积密度；（图 c）使用立体渲染技术，利用这些值得到一张图像。由于这个渲染函数是可导的，因此我们可以最小化 合成图像 和 真实观察图像 的残差，进行场景表示的优化。

• 为了根据某一视角（viewpoint），渲染出这个神经辐射场（Neural Radiance Field, NeRF），我们：

1. 1. 使相机光线穿过场景，生成一组 3D 采样点；
   2. 让这些 3D 点和对应的 3D 视角方向作为神经网络的输入，生成一组颜色和密度；
   3. 使用经典的立体渲染技术，累加这些颜色和密度，得到 2D 图像。

• 由于以上过程是可导的，我们可以使用梯度下降来优化模型，最小化 观测图像 与 模型回归计算的图像之间的误差。
  • 这可以鼓励神经网络学习的场景模型具有一致性（coherent），即在包含场景内容的位置，可以得到较大的体积密度，和准确的颜色。
• 我们发现对于复杂的场景，用简单的方法优化 NeRF 效果不理想：
  • 很难得到高分辨率的收敛结果；
  • 也不能高效利用相机光线所需的采样点。
• 于是，我们这样解决以上问题：
  • 用一个位置编码（positional encoding）对输入 5D 坐标进行变换，使得 MLP 可以表示高频函数；
  • 提出层次化的采样流程（hierarchical sampling procedure），减少所需的采样点。
• 我们的方法保留了体积表示的优点：
  • 可以表示复杂的几何和外观；
  • 可以通过投影图像进行梯度下降的优化。
• 重要的是，我们的方法克服了体积表示的一个关键问题：在表示高分辨率的复杂场景时，离散的体素网格的存储空间成本非常高。
• 总结下来，本文的贡献如下：
  • 包含复杂几何和材质的连续场景的表示方法：使用参数化为 MLP 的 5D 神经辐射场；
  • 基于立体渲染技术的可导的渲染流程，用于网络的优化。其中还包括层次化的采样策略，专注于可见的场景内容（visible scene content），充分利用了 MLP 的容量。
  • 使用位置编码，将输入 5D 坐标映射到更高维的空间，让 NeRF 可以学习表示高频的场景内容。

2 相关工作

3 神经辐射场的场景表示

我们把一个连续的场景表示为一个 5D 向量值函数（vector-valued function）：

• 输入是 3D 位置 $x=(x,y,z)$ 和 2D 视角方向 $(\theta ,\varphi )$
• 输出是发射颜色 $c=(r,g,b)$ 和体积密度 $\sigma$。

在实际中，我们把视角方向表示为 3D 笛卡尔单位向量 $d$。我们用一个 MLP 网络来近似这个连续的 5D 场景表示：
$$F_{\Theta }:(\mathbf{x},\mathbf{d})\to (\mathbf{c},\sigma )$$
我们优化该网络的权重，使之对于每个输入 5D 坐标，都会得到对应的密度和有方向的发射颜色。

我们约束了预测体积密度 σ 的网络的输入仅仅是位置 X，而预测 RGB 颜色 C 的网络的输入是位置和视角方向，通过这种方式可以鼓励网络学习到多视角连续的表示。

• 在具体实现上，MLP $F_{\Theta }$ 首先用 8 层的全连接层（使用 ReLU 激活函数，每层有 256 个通道），处理 3D 坐标 $x$，得到 $\sigma$ 和一个 256 维的特征向量。
• 这个 256 维的特征向量，与视角方向一起拼接起来，喂给另一个全连接层（使用 ReLU 激活函数，每层有 128 个通道），输出方向相关的 RGB 颜色。

图 3 可以观察到，我们的方法可以表示出非朗伯体效应（non-Lambertian effects）。从图 4 可以观察到，如果训练模型时没有视角的依赖（只有 X 一个输入），那么模型会很难表示出高光（specularity）。

Fig. 3：视角相关的发射辐射亮度。在（a）和（b），我们从不同视角定位相同位置的两个点。我们的方法可以预测两个 3D 点变化的高光现象。在图（c）中我们可以看到这个性质，在视角方向的半球上连续地呈现。

Fig. 4：展示我们的整个模型如何受益于视角相关的辐射亮度，以及如何受益于把输入坐标传入高频率位置编码的方法。如果去除视角相关性（view dependence），会导致模型失去镜面（高光）反射；如果移除位置编码，会大大降低模型表征高频几何和纹理信息的能力，导致过度平滑的外观。

4 辐射场的立体渲染

我们的 5D 神经辐射场把场景表示为：任意空间点上的体积密度和有方向的辐射亮度。使用经典的立体渲染的原理，我们可以渲染出任意射线穿过场景的颜色。体积密度 $\sigma (x)$ 可以解释为：光线停留在位置 X� 处的无穷小粒子的可导概率。在最近和最远边界为 $t_n$ 和 $t_f$ 的条件下，相机光线 $r(t)=o+td$ 的颜色 $C(r)$为：
$$\begin{array}{c}C(\mathbf{r})={\int }_{t_n}^{t_f}T(t)\sigma (\mathbf{r}(t))\mathbf{c}(\mathbf{r}(t),\mathbf{d})dt,\text{ where }T(t)=\exp \left(-{\int }_{t_n}^t\sigma (\mathbf{r}(s))ds\right)\end{array}$$

函数 $T(t) $表示沿着光线从 $t_n$ 到 $t$ 所累积的透明度（accumulated transmittance） ，即 光线从 $t_n$ 出发到 $t$，穿过该路径的概率。视图的渲染需要求这个积分 $C(r)$，它是就是虚拟相机穿过每个像素的相机光线，所得到的颜色。

我们使用求积法（quadrature）进行积分的数值求解。确定性的求积分不太适合 MLP，我们采用的是**分层抽样（stratified sampling）**的方法。我们把 $[t_n,t_f]$分成均匀分布的小区段，接着对每个小区段进行均匀采样：
$$\begin{array}{c}{t}_i\sim \mathcal{U}\left[t_n+\frac{i-1}{N}\left(t_f-t_n\right),t_n+\frac{i}{N}\left(t_f-t_n\right)\right]\end{array}$$
我们使用采样的样本，用积分法则来计算 $C(r)$：
$$\begin{array}{c}\hat{C}(\mathbf{r})=\sum _{i=1}^N{T}_i\left(1-\exp \left(-{\sigma }_i{\delta }_i\right)\right){\mathbf{c}}_i,\text{ where }{T}_i=\end{array}$$

论文笔记：NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis

论文阅读《Block-NeRF: Scalable Large Scene Neural View Synthesis》

英文文献翻译的几款实用工具

论文阅读《Point NeRF:Point-based Neural Radiance Fileds》

将外国文献翻译成中文