论文阅读《Block-NeRF: Scalable Large Scene Neural View Synthesis》

Posted 2023-04-02 CV科研随想录

论文地址：https://arxiv.org/pdf/2202.05263.pdf
复现源码：https://github.com/dvlab-research/BlockNeRFPytorch

---

概述

  Block-NeRF是一种能够表示大规模环境的神经辐射场（Neural Radiance Fields）的变体，将 NeRF 扩展到渲染跨越多个街区的城市规模场景。该方法将场景分解为单独训练的 NeRF，使渲染时间与场景大小解耦，并允许对环境进行每个街区的更新。Block-NeRF为每个单独的 NeRF 添加外观嵌入（appearance embeddings）、学习姿态优化（learned pose refinement）和可控曝光（controllable exposure），并引入了一种在相邻 NeRF 之间对齐外观（aligning appearance）方法来融合不同场景信息。

---

模型架构

  将场景分为多组Block-NeRF，每个Block可以并行独立训练，并在推理过程中进行融合。使得可以对单独的block更新而无需对整个场景进行重新训练。在此过程中，动态选择相关的 Block-NeRF 进行渲染，在跨越场景时以平滑的方式合成场景。为了实现这种平滑的合成方式，优化了Appearance代码来适应照明条件，并使用每个Block-NeRF到新视图的距离来计算插值权值。

Block 大小与位置

  在每个十字路口放置一个Block-NeRF，覆盖十字路口本身与任意连接街道的75%的场景，使得任何两个相邻的街区之间有50%的场景重叠。

独立Block-NeRF的训练过程

外观编码：使用 MLP 来学习不同外观变化的条件，如不同的天气与光照条件。还可以通过控制外观编码（appearance embedding）来对不同环境进行线性插值，得到不同条件下的环境信息（如多云和晴朗的天空，或者白天与晚上），如图3与图4所示：

位姿优化：Learned Pose Refinement是通过在每个Block-NeRF中训练一个额外的神经网络来实现的，这个神经网络可以根据输入的图像和初始的相机姿态，输出一个修正后的相机姿态。使得Block-NeRF就可以利用更准确的相机姿态来生成更高质量的新视角图像。
输入图像曝光：将相机曝光信息输入到模型的外观预测部分，使得NeRF补偿视觉上的差异，使用 4 层的 $sin$ 来对曝光信息进行编码。

瞬态（移动）物体：Transient Objects是指在训练图像中出现的临时物体，如行人、车辆等，它们会影响Block-NeRF学习场景的静态结构，因为它们会导致视角不一致。通过以下步骤来消除场景中的瞬态物体的影响：

• 首先，对于每个训练图像，使用一个分割算法来检测并去除Transient Objects，得到一个纯净的背景图像。
• 然后，对于每个Block-NeRF，使用去除了Transient Objects的背景图像来训练神经网络，从而学习场景的静态结构。
• 最后，在渲染新视角图像时，使用原始的训练图像（包含Transient Objects）作为输入，并将分割算法得到的掩码作为额外的输入送入Block-NeRF中，从而在输出图像中保留或去除Transient Objects。
  这样做的好处是，Block-NeRF可以灵活地处理不同场景下的Transient Objects，并且可以在渲染时根据用户需求选择是否显示它们。
  场景可见性预测：Visibility Prediction的具体实现是这样的：
• 首先，对于每个Block-NeRF，构建一个小的多层感知机（MLP）$f_v$ ，以位置信息 $x$ 和方向信息 $d$ 作为输入，用来学习样本点可见性的近似值。
• 然后，对于每个Block-NeRF，使用其训练图像中的采样点作为输入，计算其可见性近似值，并将其与由密度函数得到的透射率$T_i$作为监督信号进行训练。
• 最后，在合并多个Block-NeRF时，使用 $f_v$ 来判断一个给定的场景区域是否对该Block-NeRF可见，并根据可见性近似值来加权不同Block-NeRF的输出颜色。
  Visibility Prediction可以有效地解决不同Block-NeRF之间的遮挡问题，并且可以提高渲染质量和效率。

Block_Nerf合并

Block-NeRF选择：一个大型场景由多个 Block 组成，Block-NeRF使用两种策略进行Block选择（1）只考虑在目标视点设定半径范围内的Block-NeRF。（2）计算每个候选Block的相关可见性，如果平均可见性小于阈值，则舍弃该Block。如图2所示，可见性可以由一个独立的模块计算，且不需要在目标图像的分辨率下进行渲染。通过筛选，通常剩余1-3个Block-NeRF有待合并。
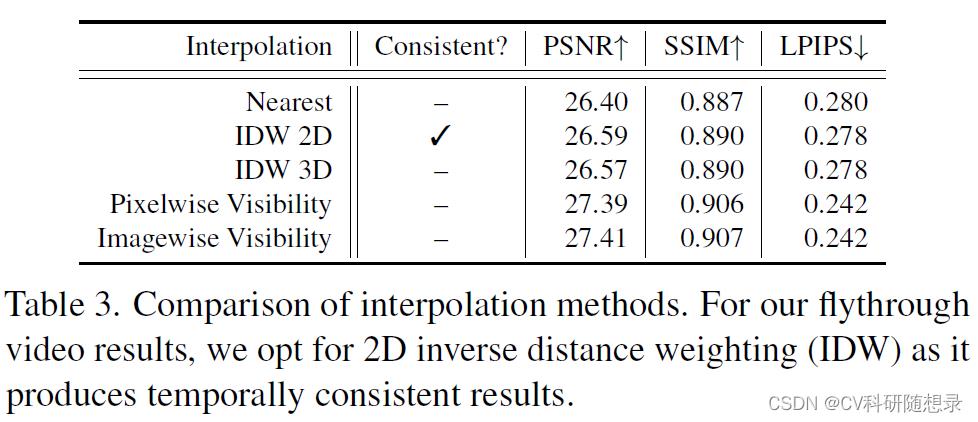
Block-NeRF合成：使用相机原点 $c$ 与每个Block-NeRF 的中心 $x_i$ 之间的逆距离加权系数对候选 Block 插值（$w_i\propto distance(c,x_i{)}^{-p}$, $p$ 影响Block之间的混合速率）。插值在二维图像中进行，在不同Block-NeRF之间产生平滑的过渡。
场景外观匹配：

Appearance Matching是为了在不同block之间消除外观上的不一致性，使得渲染结果更加自然和真实。具体步骤如下：

• 对于每个block，为其分配一个外观编码（appearance code），这是一个随机初始化的向量，用于控制block的颜色和光照。
• 对于每对相邻的block，选择一个三维区域作为匹配位置（matching location），这个区域要求在两个block中都有较高的可见度。
• 对于每个匹配位置，冻结两个block对应的NeRF网络的权重，只优化其中一个block的外观编码，使得两个block在该位置渲染出来的颜色值之间的L2损失最小。
• 重复上述步骤，直到所有相邻的block都进行了外观匹配。
  以此实现大场景中不同block之间外观上的对齐，如图6所示。

---

实验结果

论文阅读|node2vec: Scalable Feature Learning for Networks

论文阅读|node2vec: Scalable Feature Learning for Networks

文章目录

• • 论文阅读|node2vec: Scalable Feature Learning for Networks
  • • Abstract
    • Introduction
    • Feature Learning Framework
    • • Classic search strategies
      • node2vec
    • 参考资料

Abstract

Node2vec:一种用于学习网络中节点的连续特征表示的算法框架。学习节点到低维特征空间的映射，以最大化保留节点网络领域概念，并设计了一个baised（偏向）随机游走过程，有效探索不同的领域。

---

Introduction

任何有监督的机器学习算法都需要一组信息丰富的、有辨别力的和独立的特征。 在网络的预测问题中，这意味着必须为节点和边构建特征向量表示。 非典型解决方案涉及基于专业知识的手工工程特定领域特征。 即使不考虑特征工程所需的繁琐工作，这些特征通常是为特定任务设计的，并且不会在不同的预测任务中泛化。另一种方法是通过解决优化问题来学习特征表示。 特征学习的挑战在于定义目标函数，这涉及平衡计算效率和预测准确性的权衡。

node2vec 可以学习根据节点的网络角色或它们所属的社区组织节点的表示。 通过开发一系列有偏随机游走来实现这一点，它可以有效地探索给定节点的不同邻域。

贡献如下：

• 提出了 node2vec，这是一种用于网络中特征学习的高效可扩展算法，可使用 SGD 有效优化新的网络感知、邻域保留目标。
• 算法的灵活性，适用于等价网络？
• 扩展了node2vec和其他基于邻域保留目标的特征学习方法，从节点到节点对，用于基于边的预测任务。
• 应用于现实网络中进行多标签分类和链路预测

---

Feature Learning Framework

$f:V\to R^d$，d为特征维度，f为大小为$|V|$的矩阵，对于每个源节点 $u\in V$ ，我们将 $N_S(u)\subset V$ 定义为通过邻域采样策略 S 生成的节点 u 的网络邻域。

优化以下目标函数：
$$ma{x}_f\sum _{u\in V}logPr(N_S(u)|f(u))$$
为优化问题易于处理，论文中做出两个标准假设：

• 有条件的独立。 我们通过假设观察邻域节点的可能性独立于给定源的特征表示观察任何其他邻域节点来分解似然：
  $$Pr(N_S(u)|f(u))=\prod _{n_i\in N_S(u)}Pr(n_i|f(u))$$

• 特征空间中的对称性。 源节点和邻域节点在特征空间中彼此具有对称效应。 对条件似然进行建模，每个源-邻域节点对作为由其特征的点积参数化的softmax单元：
  $$Pr(n_i|f(u))=\frac{exp(f(n_i)\cdot f(u))}{{\sum }_{v\in exp(f(v)\cdot f(u)}}$$

通过上述假设，目标函数可简化为
$$ma{x}_f\sum _{u\in V}[-log{Z}_u+\sum _{n_i\in N_S(u)}f(n_i)\cdot f(u)]$$

Classic search strategies

论文将源节点的邻域采样问题视为一种局部搜索形式。对于上图中的源结点u，我们的目标是生成（采样）其邻域$N_S(u)$。为了采样策略的公平，将邻域$N_S(u)$的大小限制为k个节点，然后为单个节点u采样多个集。通常，生成k个节点的邻域$N_S$有两种极端采样策略：

• Breadth-first Samping（BFS）
• Depth-first Samping（DFS）

BFS体现了网络结构的微观等效性；

DFS体现了网络结构的宏观等效性；

node2vec

Random Walks（随机游走）

通常，给定一个源结点u，游走长度固定为$l$,$c_i$表示游走的第i个节点，令初始节点为$c_0=u$，节点$c_i$由以下分布生成：
$$P(c_i=x|c_{i-1}=v)=\{\begin{array}{l}\frac{{\pi }_{vx}}{Z},if(v,x)\in E\\ 0,otherwise\end{array}$$
其中${\pi }_{vx}$是节点v和x之间的非归一化转移概率，Z是归一化常数。

Search bias α（有偏搜索α）

带有两个参数p和q的二阶随机游走，考虑一个游走，它刚刚遍历了边（t，v），现在位于图中节点v。步行现在需要决定下一步，此时评估从v开始的边**（v，x）上的转移概率${\pi }_{vx}$。将非归一化转移概率设置为${\pi }_{vx}=\alpha pq(t,x)\cdot w_{vx}$，其中
$${\alpha }_{pq}(t,x)=\{\begin{array}{l}\frac{1}{p},if{d}_{tx}=0\\ 1,if{d}_{论文阅读|node2vec:\; Scalable\; Feature\; Learning\; for\; Networks}\end{array}$$

论文阅读｜深读node2vec: Scalable Feature Learning for Networks

论文阅读：Fast, Scalable, and Programmable Packet Scheduler in Hardware

阅读报告：Scalable Processing of Contemporary Semi-Structured Data

论文精读：XGBoost: A Scalable Tree Boosting System

论文精读：XGBoost: A Scalable Tree Boosting System