深度学习之线性代数

Posted 2022-07-04 彭祥.

这里主要介绍一些张量的计算，如求和，转置等
标量运算

import torch
x=torch.tensor(3.0)
y=torch.tensor(4.0)
print(x*y,x+y,x-y,x**y,x/y)#这种单一元素(标量)可以进行各种四则运算等
print(x.shape)

矩阵转置

import torch
x=torch.arange(20).reshape(5,4)
print(x)
print(x.t())#矩阵转置
B = torch.tensor([[1, 2, 3], [2, 0, 4], [3, 4, 5]])
print(B)
print(B==B.t())#对称矩阵转置后与原矩阵相同

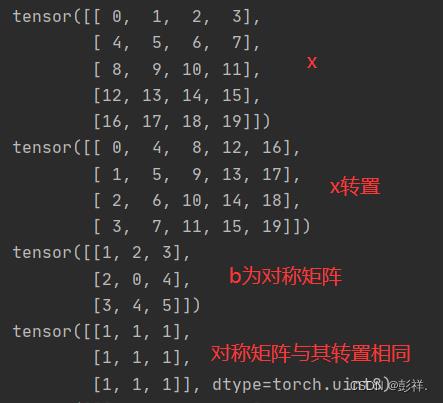
关于python中的赋值，其只是将地址赋给了某个变量，当其改变时，会一同改变，可使用y=x.clone()来重新生成数据

#降维
import torch
A = torch.arange(12, dtype=torch.float32).reshape(3,4)
A_sum_axis0 = A.sum([1])#0为按列求和，1为按行求和，[0,1]为全部,此时即实现了降维
print(A,A_sum_axis0, A_sum_axis0.shape)
A = torch.arange(24, dtype=torch.float32).reshape(2,3,4)
sum_A = A.sum(1)#3维时则丢掉了一个变为一个维度，即丢失行维度，同理，0为丢失第一个，2为第三个
print(A_sum_axis0)
print(A)

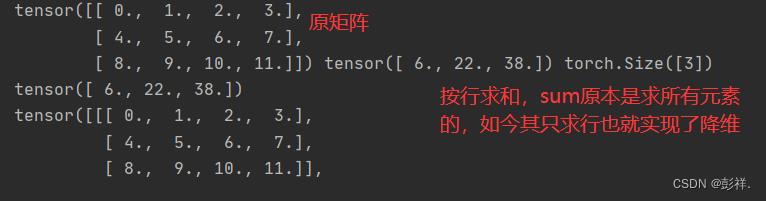
keepdims会将维度不降而变成一

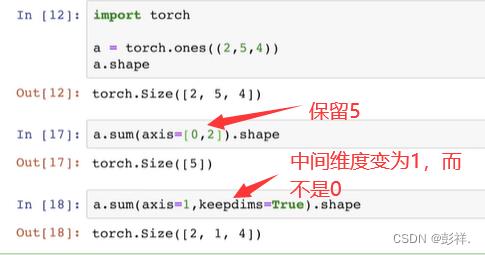
累加求和

import torch
A = torch.arange(12, dtype=torch.float32).reshape(3,4)
A_sum_axis0=A.cumsum(0)
print(A)
print(A_sum_axis0)

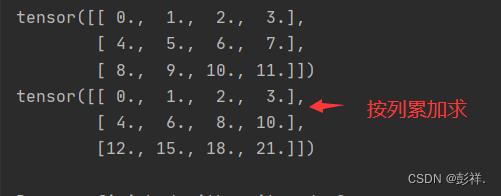
import torch
y = torch.ones(4, dtype = torch.float32)
print(y)
print(torch.dot(y,y))#向量点积
y = torch.ones(4, dtype = torch.float32)
x=torch.arange(12,dtype = torch.float32).reshape(3,4)
print(torch.mv(x,y))#向量*矩阵
B = torch.ones(4, 3)
print(torch.mm(x, B))#矩阵*矩阵