人工智能深度学习入门练习之(12)TensorFlow – 数学基础
Posted huanghanyu
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了人工智能深度学习入门练习之(12)TensorFlow – 数学基础相关的知识,希望对你有一定的参考价值。
在创建TensorFlow中的应用程序之前,最好能先理解TensorFlow所需的数学概念。数学被认为是任何机器学习算法的核心。
线性代数
- 标量(scalar) 一个单独的数
- 向量(vector) 一列数,即一维数组
- 矩阵(matrix) 二维数组
- 张量(tensor) 多维数组
矩阵加法
如果2个矩阵维数相同,则这2个矩阵可以相加。矩阵相加时,2个矩阵对应位置的元素进行相加。
示例
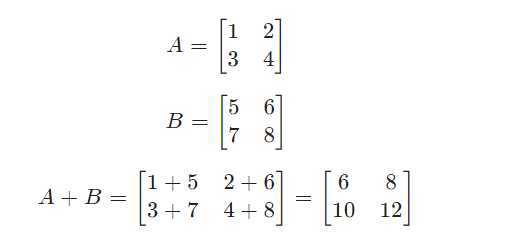
矩阵减法
矩阵减法与矩阵加法类似,2个维数相同的矩阵,对应位置元素进行相减运算。
示例
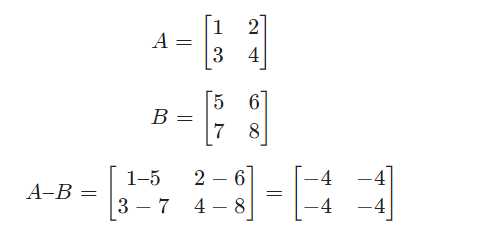
矩阵乘法
2个矩阵相乘,跟加减法稍有不同,不是对应元素相乘。
假设矩阵A (形状m x n) 与 B (形状p x q)相乘,必须n = q,即A的列数必须与B的行数相同,得到的结果是C(形状m x q),其中元素的算法如下:
示例
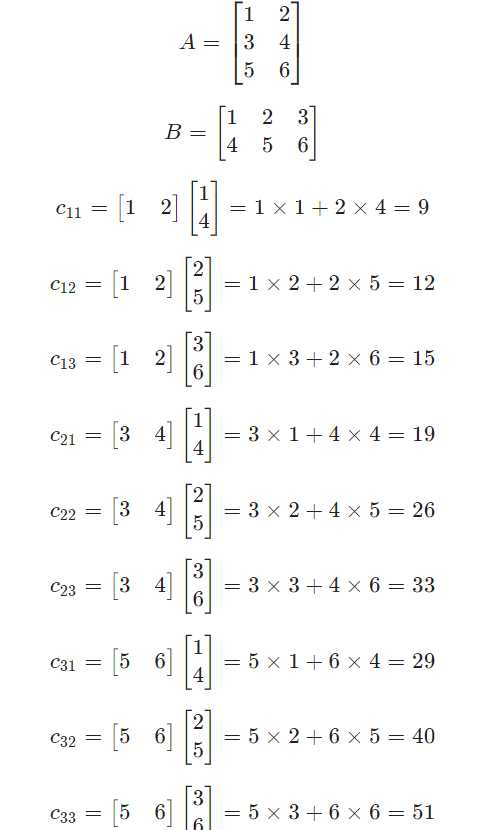

矩阵转置
矩阵转置是指把一个矩阵的列转置为行得到一个新矩阵,矩阵A的转置可以表示为A^TAT。
示例
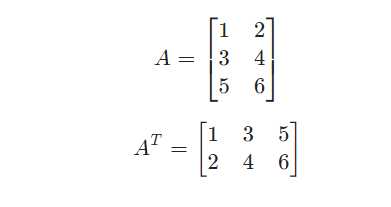
向量点积
向量是一维数组,2个长度相同的向量可以求点积。点积是指2个长度相同的向量,对应元素相乘然后再相加得到的值。
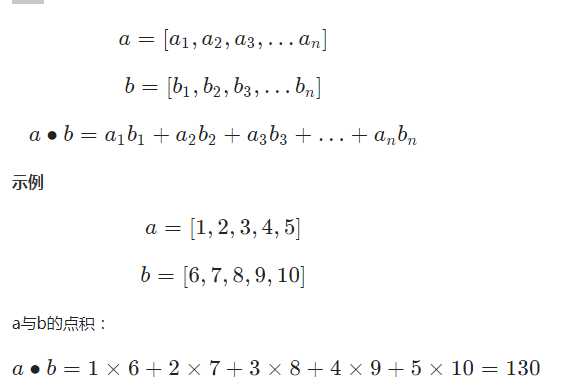
以上是关于人工智能深度学习入门练习之(12)TensorFlow – 数学基础的主要内容,如果未能解决你的问题,请参考以下文章