k近邻&kd树

Posted 2023-03-27

参考技术A

k近邻算法是懒惰学习的代表算法。之所以说k近邻懒惰，是因为它没有显示的训练过程。它的思路很简单， 手头有一些带标签的样本，现在给定一个新的样本，找出已有样本中距离新样本最近的k个样本点，然后取这k个样本点标签的投票结果。

k近邻算法本身并不复杂，但有几个细节需要注意：

（1）距离度量

不同的距离度量可能产生不同的k近邻，从而直接影响预测结果。至于度量的选取要结合应用场景， 关键在于我们需要知道在特定场景中如何量化两样本之间的相似度。

（2）k值选择

k值的选择没有经验性的方法，一般只能通过交叉验证来选取合适的k值。

如果k值选择较小，就相当于用较小的邻域中的训练实例进行预测，“学习”的近似误差会减小，只有与输入实例较近的训练实例才会对预测起作用，但估计误差会增大，预测结果会对近邻的实例点非常敏感，如果近邻的实例点恰巧是噪声，预测就会出错。相反如果k值选择较大，就相当于用较大的领域中的训练实例进行预测，近似误差会增大，但估计误差会减小。

对于k近邻法来说，k越大模型越简单，这一点乍一看不容易理解，但其实我们可以考虑极端情况k=N（N为样本数），此时任何新样本都会被归入当前样本集中实例最多的类别，从而丢失大量信息。反之，k越小模型越复杂，模型将面临过拟合风险。

（3）投票法

k近邻使用多数表决的投票法看起来十分自然，但我们也可以从 最小化经验误差 的角度来理解，如果分类的损失函数为0-1损失函数，则误分类概率为：

对于给定实例 ，其最近邻的k个训练实例构成集合 ，若涵盖 的区域的类别是 ，则误分类概率为：

要使误分类率最小即经验风险最小，就要使 最大，这正是投票法（多数表决）所做的事情。

kd树是一种对k维空间中的实例点进行储存以便对其进行快速检索的树形数据结构。 kd树是二叉树，表示对k维空间的一个划分。构造kd树相当于不断用垂直于坐标轴的超平面将k维空间切分，构成一系列k维超矩形区域。

构造平衡kd树的流程 如下：

输入：k维空间数据集

（1）构造根结点，根结点对应于包含 的k维空间的超矩形区域。

（2）对深度为 的结点，选择 为切分的坐标轴（ ），以该结点区域中所有实例的 坐标的中位数为切分点，将该结点对应的超矩形区域划分为两个子区域，切分由通过切分点并与坐标轴 垂直的超平面实现。

（3）重复（2）直至划分得到的两个子区域中没有实例存在为止。

用kd树进行最近邻搜索的流程 如下：

输入：构造好的kd树，目标节点x

（1）在kd树中找到包含目标节点 的叶结点：从根结点出发，递归地向下访问kd树。若目标 当前维的坐标小于切分点坐标则移动到左子结点，否则移动到右子结点，直至子结点为叶结点为止。

（2）以此叶结点为“当前最近点”。

（3）递归地向上回退：

（4）当回退到根结点，搜索结束，此时的“当前最近点”即为 的最近邻点。

以上就是利用kd树进行最近邻搜索的过程，同样的方法可以推广到k近邻。现在我们来思考一下这个算法的本质。

其实我个人理解的是， kd树的构造就是二分法在k维的应用。 但是不太相同的是，kd树算法并不是选定一个轴后不断二分直至结束，而是做一次二分换一个轴，这是因为如果我们只选定一个轴做二分得到的结果并不能反映各样本之间距离的远近，而兼顾各个轴则能一定程度上度量样本之间的距离。

我们可以想象3维的情况，kd树最终会形成一系列的小正方体，我们要想找距离一个新样本点最近的样本点，只需要找到新样本点所在的小正方体，然后check这个小正方体中的样本以及和这个小正方体 相邻 的小正方体中的样本哪个距离新样本最近即可（相邻这个概念是很重要的，为便于理解，考虑在一维的情况下，此过程为找到新样本所在区间，然后检查此区间以及左右相邻区间中的样本点即可）。而 相邻 这个概念刚好和kd树的构造过程相符，我们不断回退的过程其实就是检查 各个不同方向上 的相邻超矩形的过程。这个过程十分高效，不难看出，平衡kd树寻找最近邻的复杂度是 。

机器学习k近邻算法kd树实现优化查询

目录

• 1 kd树简介
• • 1.1 什么是kd树
  • 1.2 原理
• 2 构造方法
• 3 案例分析
• • 3.1 树的建立
  • 3.2 最近领域的搜索
  • • 3.2.1 查找点(2.1,3.1)
    • 3.2.2 查找点(2,4.5)
• 4 总结

---

1 kd树简介

1.1 什么是kd树

问题导入：

实现k近邻算法时，主要考虑的问题是如何对训练数据进行快速k近邻搜索。

这在特征空间的维数大及训练数据容量大时尤其必要。

**k近邻法最简单的实现是线性扫描（穷举搜索），即要计算输入实例与每一个训练实例的距离。计算并存储好以后，再查找K近邻。**当训练集很大时，计算非常耗时。

为了提高kNN搜索的效率，可以考虑使用特殊的结构存储训练数据，以减小计算距离的次数。

根据KNN每次需要预测一个点时，我们都需要计算训练数据集里每个点到这个点的距离，然后选出距离最近的k个点进行投票。当数据集很大时，这个计算成本非常高，针对N个样本，D个特征的数据集，其算法复杂度为O（DN2）。

kd树：为了避免每次都重新计算一遍距离，算法会把距离信息保存在一棵树里，这样在计算之前从树里查询距离信息，尽量避免重新计算。其基本原理是，如果A和B距离很远，B和C距离很近，那么A和C的距离也很远。有了这个信息，就可以在合适的时候跳过距离远的点。

这样优化后的算法复杂度可降低到O（DNlog（N））。感兴趣的读者可参阅论文：Bentley，J.L.，Communications of the ACM（1975）。

1989年，另外一种称为Ball Tree的算法，在kd Tree的基础上对性能进一步进行了优化。感兴趣的读者可以搜索Five balltree construction algorithms来了解详细的算法信息。

1.2 原理

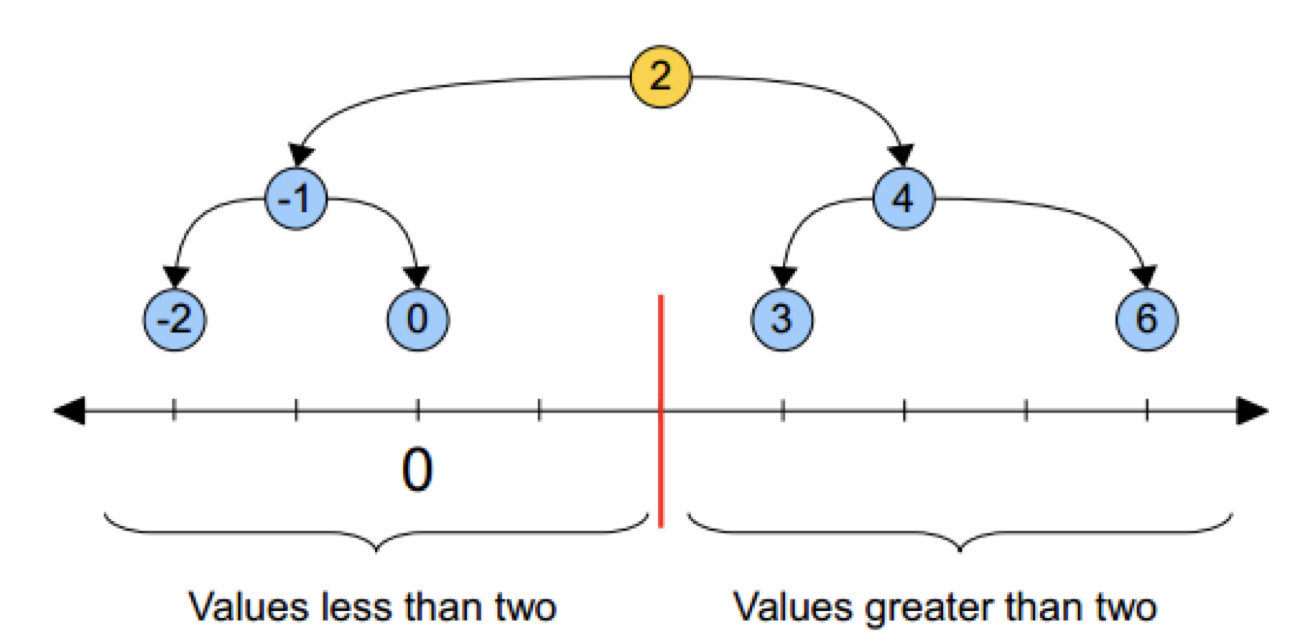
黄色的点作为根节点，上面的点归左子树，下面的点归右子树，接下来再不断地划分，分割的那条线叫做分割超平面（splitting hyperplane），在一维中是一个点，二维中是线，三维的是面。

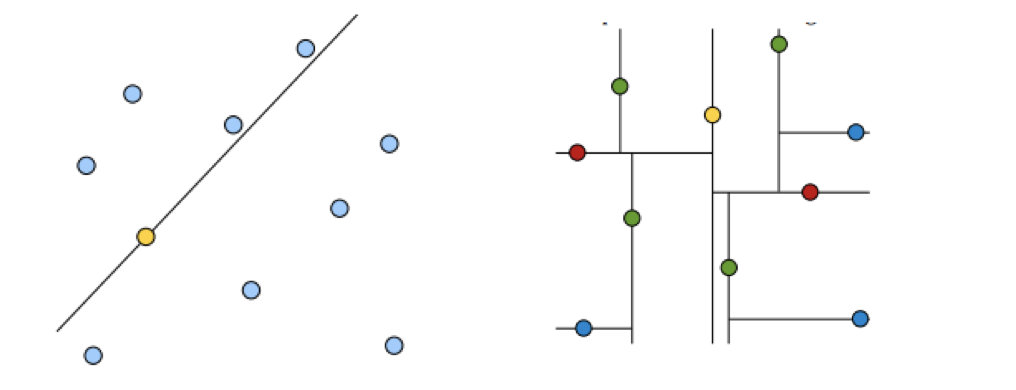
黄色节点就是Root节点，下一层是红色，再下一层是绿色，再下一层是蓝色。

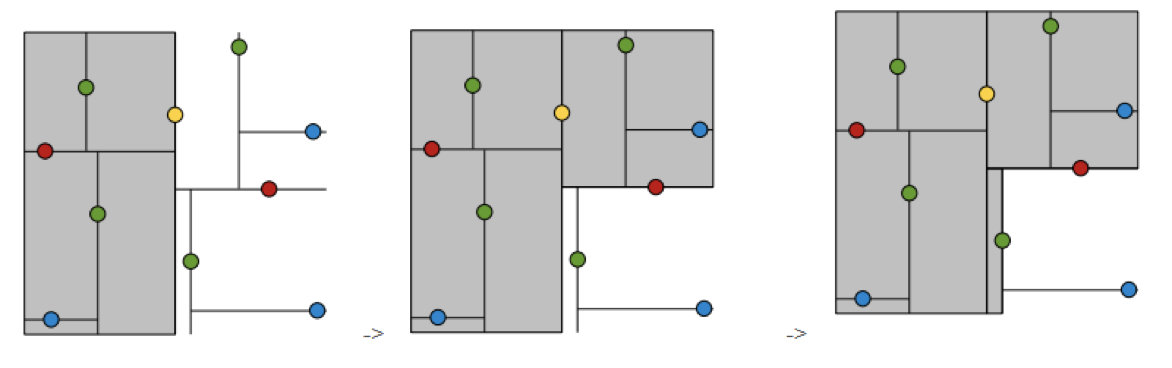
1.树的建立；

2.最近邻域搜索（Nearest-Neighbor Lookup）

kd树(K-dimension tree)是**一种对k维空间中的实例点进行存储以便对其进行快速检索的树形数据结构。**kd树是一种二叉树，表示对k维空间的一个划分，构造kd树相当于不断地用垂直于坐标轴的超平面将K维空间切分，构成一系列的K维超矩形区域。kd树的每个结点对应于一个k维超矩形区域。利用kd树可以省去对大部分数据点的搜索，从而减少搜索的计算量。

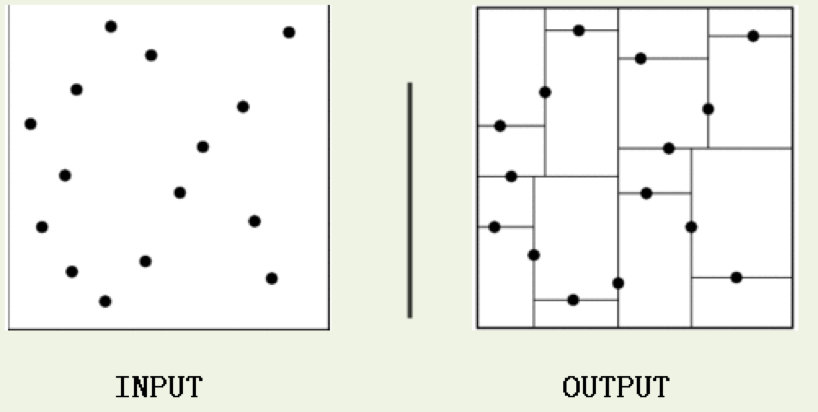
类比“二分查找”：给出一组数据：[9 1 4 7 2 5 0 3 8]，要查找8。如果挨个查找（线性扫描），那么将会把数据集都遍历一遍。而如果排一下序那数据集就变成了：[0 1 2 3 4 5 6 7 8 9]，按前一种方式我们进行了很多没有必要的查找，现在如果我们以5为分界点，那么数据集就被划分为了左右两个“簇” [0 1 2 3 4]和[6 7 8 9]。

因此，根本就没有必要进入第一个簇，可以直接进入第二个簇进行查找。把二分查找中的数据点换成k维数据点，这样的划分就变成了用超平面对k维空间的划分。空间划分就是对数据点进行分类，“挨得近”的数据点就在一个空间里面。

2 构造方法

（1）构造根结点，使根结点对应于K维空间中包含所有实例点的超矩形区域；

（2）**通过递归的方法，不断地对k维空间进行切分，生成子结点。**在超矩形区域上选择一个坐标轴和在此坐标轴上的一个切分点，确定一个超平面，这个超平面通过选定的切分点并垂直于选定的坐标轴，将当前超矩形区域切分为左右两个子区域（子结点）；这时，实例被分到两个子区域。

（3）上述过程直到子区域内没有实例时终止（终止时的结点为叶结点）。在此过程中，将实例保存在相应的结点上。

（4）通常，循环的选择坐标轴对空间切分，选择训练实例点在坐标轴上的中位数为切分点，这样得到的kd树是平衡的（平衡二叉树：它是一棵空树，或其左子树和右子树的深度之差的绝对值不超过1，且它的左子树和右子树都是平衡二叉树）。

KD树中每个节点是一个向量，和二叉树按照数的大小划分不同的是，KD树每层需要选定向量中的某一维，然后根据这一维按左小右大的方式划分数据。在构建KD树时，关键需要解决2个问题：

（1）选择向量的哪一维进行划分；

（2）如何划分数据；

第一个问题简单的解决方法可以是随机选择某一维或按顺序选择，但是更好的方法应该是在数据比较分散的那一维进行划分（分散的程度可以根据方差来衡量）。

第二个问题中，好的划分方法可以使构建的树比较平衡，可以每次选择中位数来进行划分。

3 案例分析

3.1 树的建立

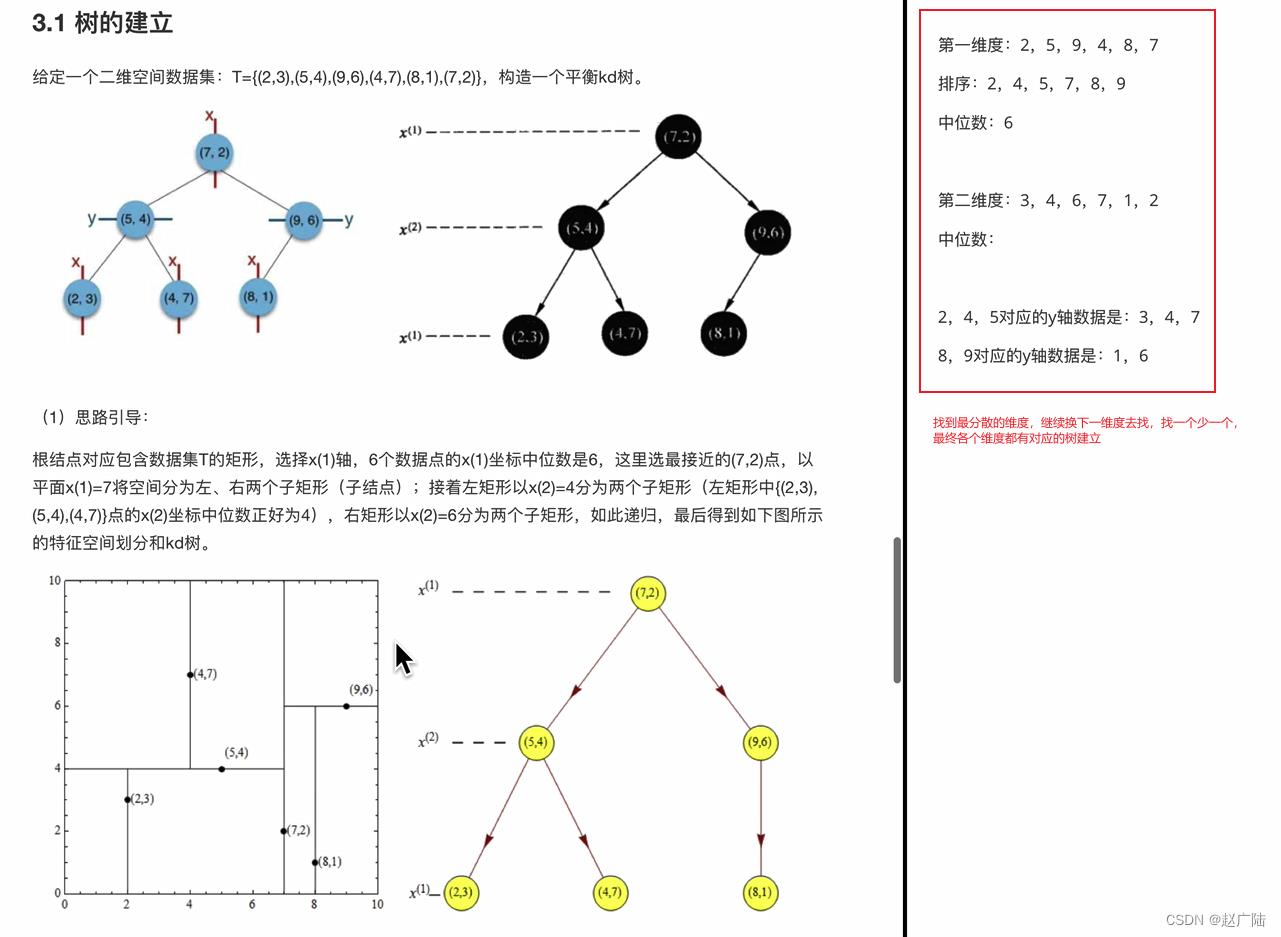
给定一个二维空间数据集：T=(2,3),(5,4),(9,6),(4,7),(8,1),(7,2)，构造一个平衡kd树。

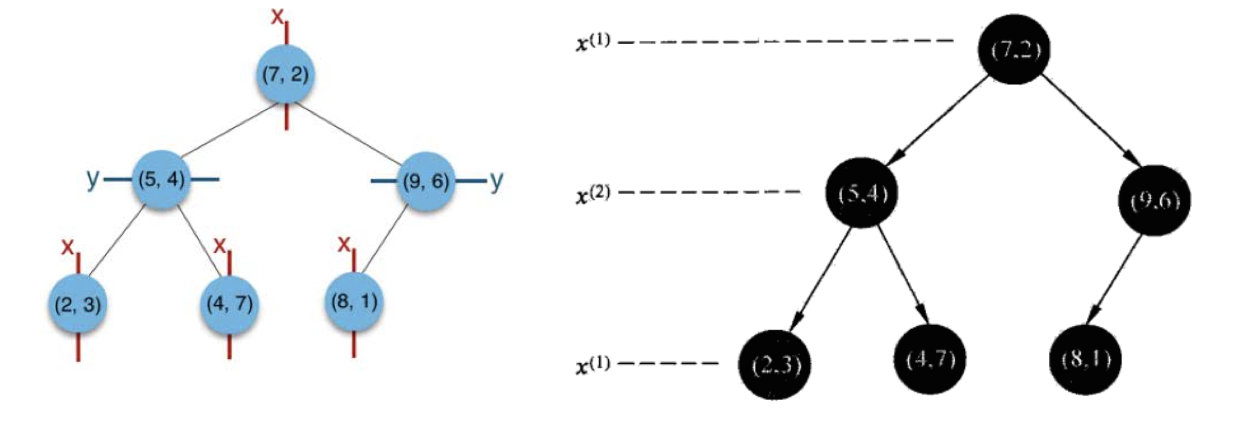
（1）思路引导：

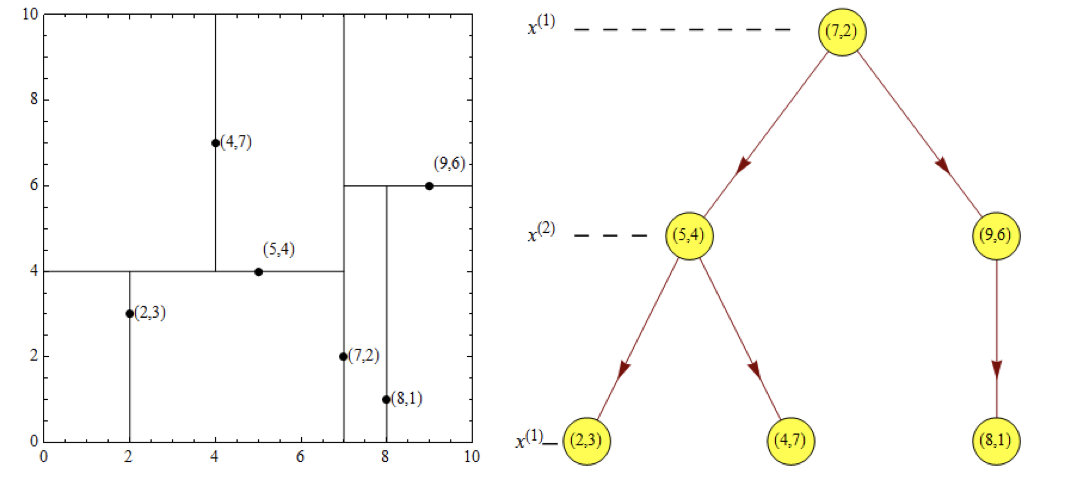
根结点对应包含数据集T的矩形，选择x(1)轴，6个数据点的x(1)坐标中位数是6，这里选最接近的(7,2)点，以平面x(1)=7将空间分为左、右两个子矩形（子结点）；接着左矩形以x(2)=4分为两个子矩形（左矩形中(2,3),(5,4),(4,7)点的x(2)坐标中位数正好为4），右矩形以x(2)=6分为两个子矩形，如此递归，最后得到如下图所示的特征空间划分和kd树。

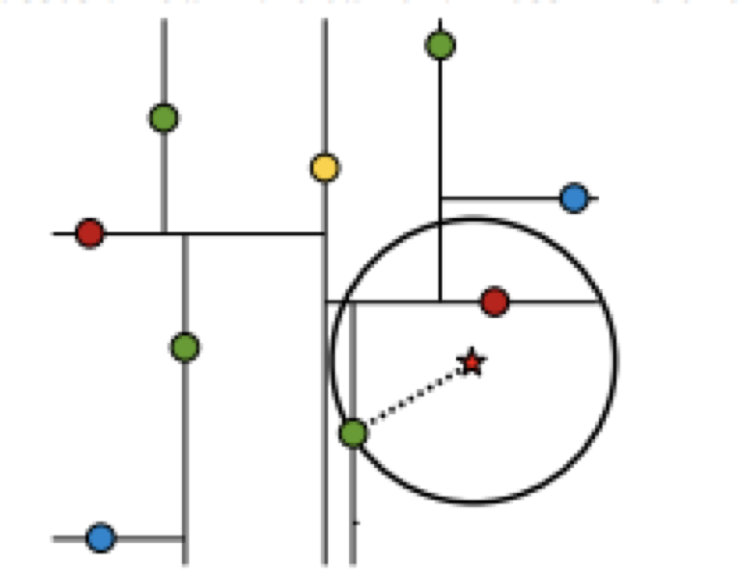
3.2 最近领域的搜索

假设标记为星星的点是 test point， 绿色的点是找到的近似点，在回溯过程中，需要用到一个队列，存储需要回溯的点，在判断其他子节点空间中是否有可能有距离查询点更近的数据点时，做法是以查询点为圆心，以当前的最近距离为半径画圆，这个圆称为候选超球（candidate hypersphere），如果圆与回溯点的轴相交，则需要将轴另一边的节点都放到回溯队列里面来。

样本集(2,3),(5,4), (9,6), (4,7), (8,1), (7,2)

3.2.1 查找点(2.1,3.1)

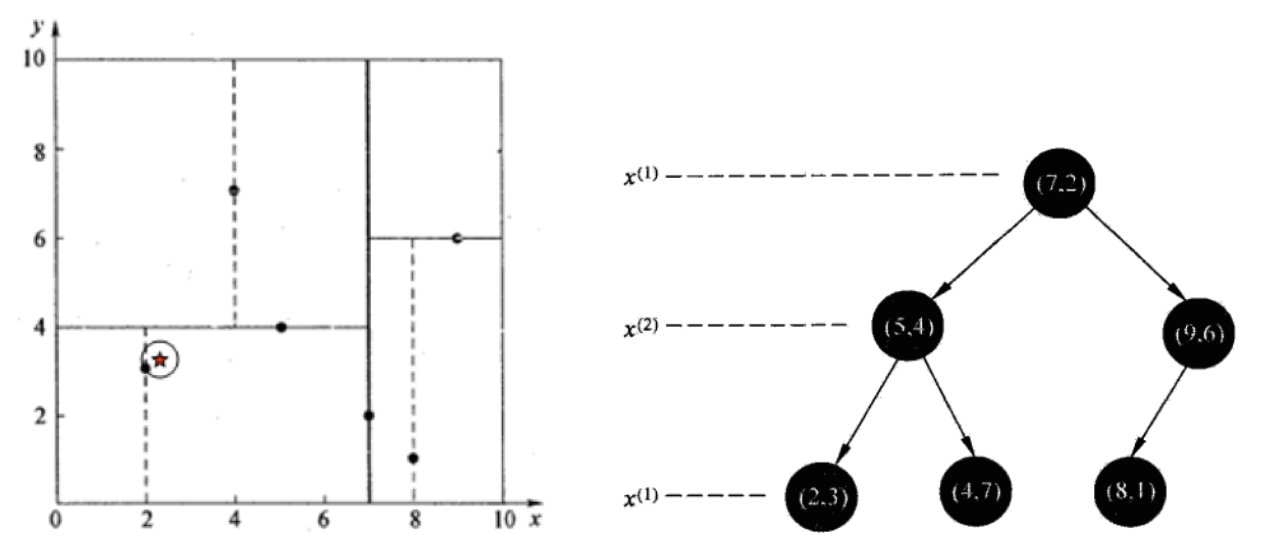
在(7,2)点测试到达(5,4)，在(5,4)点测试到达(2,3)，然后search_path中的结点为<(7,2),(5,4), (2,3)>，从search_path中取出(2,3)作为当前最佳结点nearest, dist为0.141；

然后回溯至(5,4)，以(2.1,3.1)为圆心，以dist=0.141为半径画一个圆，并不和超平面y=4相交，如上图，所以不必跳到结点(5,4)的右子空间去搜索，因为右子空间中不可能有更近样本点了。

于是再回溯至(7,2)，同理，以(2.1,3.1)为圆心，以dist=0.141为半径画一个圆并不和超平面x=7相交，所以也不用跳到结点(7,2)的右子空间去搜索。

至此，search_path为空，结束整个搜索，返回nearest(2,3)作为(2.1,3.1)的最近邻点，最近距离为0.141。

3.2.2 查找点(2,4.5)

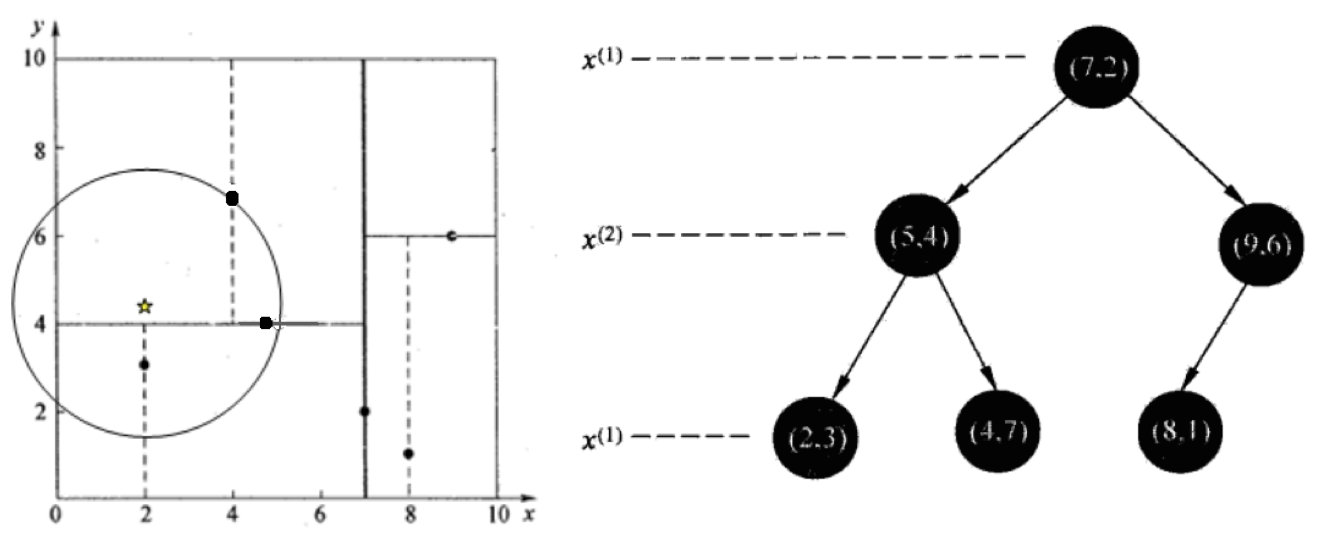
在(7,2)处测试到达(5,4)，在(5,4)处测试到达(4,7)【优先选择在本域搜索】，然后search_path中的结点为<(7,2),(5,4), (4,7)>，从search_path中取出(4,7)作为当前最佳结点nearest, dist为3.202；

然后回溯至(5,4)，以(2,4.5)为圆心，以dist=3.202为半径画一个圆与超平面y=4相交，所以需要跳到(5,4)的左子空间去搜索。所以要将(2,3)加入到search_path中，现在search_path中的结点为<(7,2),(2, 3)>；另外，(5,4)与(2,4.5)的距离为3.04 < dist = 3.202，所以将(5,4)赋给nearest，并且dist=3.04。

回溯至(2,3)，(2,3)是叶子节点，直接平判断(2,3)是否离(2,4.5)更近，计算得到距离为1.5，所以nearest更新为(2,3)，dist更新为(1.5)

回溯至(7,2)，同理，以(2,4.5)为圆心，以dist=1.5为半径画一个圆并不和超平面x=7相交, 所以不用跳到结点(7,2)的右子空间去搜索。

至此，search_path为空，结束整个搜索，返回nearest(2,3)作为(2,4.5)的最近邻点，最近距离为1.5。

4 总结

• kd树的构建过程
  • 1.构造根节点
  • 2.通过递归的方法，不断地对k维空间进行切分，生成子节点
  • 3.重复第二步骤，直到子区域中没有实例时终止
  • 需要关注细节：a.选择向量的哪一维进行划分；b.如何划分数据
• kd树的搜索过程【知道】
  • 1**.二叉树搜索比较待查询节点和分裂节点的分裂维的值**，（小于等于就进入左子树分支，大于就进入右子树分支直到叶子结点）
  • 2.顺着“搜索路径”找到最近邻的近似点
  • 3.回溯搜索路径，并判断搜索路径上的结点的其他子结点空间中是否可能有距离查询点更近的数据点，如果有可能，则需要跳到其他子结点空间中去搜索
  • 4.重复这个过程直到搜索路径为空