Miller Rabin算法的在应用中的考虑

Posted 2023-03-25

参考技术A

(i)　　(ii)　　p k ,1　　pk , t　　k 2 4 2　　k 3 / 2 2 tk　　for k 2　　t 1 / 2 4 2 tk　　(iii) p 7 k 2 5t k , t20　　1 k15 / 4 27　　k / 2 2 t　　12 k 2　　k / 4 3t　　for k / 9　　(iv) pk , t　　t k / 4, k　　1 k15 / 4 2　　7　　21　　k / 2　　2t for t　　k / 4, k 21　　Miller-Rabin算法的应用主要集中在构建密码安全体系的素数生成模块中，当输入的待测数n是很大(例如： 1024bits)的随机数的时候，算法的误判概率远远小于上面给出的理论 上的误判概率上界。设Pk,t 代表(k=log2 n，t是测试的轮数)在 素数生成算法中应用t轮Miller-Rabin 算法给出错误结果的概 率，则有如上所示的误判概率公式。　　在一般的密码安全体系中，误判概率小于 (1/2)就可以满足安全需求。表2给出了当p(k,t) ≤ (1/2)80的时候对应的k和t的值。
表2 k,t对应值 k 100 150 200 25 300 350 400 450 550 650 850 1300 t 27 18 15 12 9 8 7 6 5 4 3 2 在基底的选择上，因为以2作为基底可以剔除很大部分 合数，并且对以2为底的模幂的运算很快，所以可以考虑在 应用中固定使用基底2，其它基底随机选择，这样的改进可 以提高算法的运行速度。

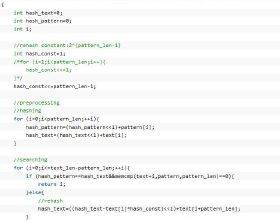
Pollard rho算法+Miller Rabin算法 BZOJ 3668 Rabin-Miller算法

BZOJ 3667: Rabin-Miller算法

Time Limit: 60 Sec  Memory Limit: 512 MB
Submit: 1044  Solved: 322
[Submit][Status][Discuss]

Description

 

Input

第一行：CAS,代表数据组数（不大于350），以下CAS行，每行一个数字，保证在64位长整形范围内，并且没有负数。你需要对于每个数字：第一，检验是否是质数，是质数就输出Prime 
第二，如果不是质数，输出它最大的质因子是哪个。 

Output

第一行CAS(CAS<=350，代表测试数据的组数) 
以下CAS行：每行一个数字，保证是在64位长整形范围内的正数。 
对于每组测试数据：输出Prime，代表它是质数，或者输出它最大的质因子，代表它是和数 

Sample Input

6
2
13
134
8897
1234567654321
1000000000000

Sample Output

Prime
Prime
67
41
4649
5

HINT

 

数据范围： 

保证cas<=350，保证所有数字均在64位长整形范围内。 

分析：虽然题目叫做Miller rabin算法，不过真正上也需要Pollard rho算法

  1 /*貌似这个代码在BZOJ上的评测器就会运行错误，但是在POJ上一道原题却通过了（POJ上语言选C++可以过，选择G++就过不了）*/
  2 #include<iostream>
  3 using namespace std;
  4 #include<cstdio>
  5 #define S 10
  6 #include<cstdlib>
  7 #include<ctime>
  8 #define ll long long
  9 ll cas, maxz=-1;
 10 ll read()
 11 {
 12     ll ans=0;char c;
 13     c=getchar();
 14     while(c<‘0‘||c>‘9‘) c=getchar();
 15     while(c>=‘0‘&&c<=‘9‘) 
 16     {
 17         ans=ans*10+c-‘0‘;
 18         c=getchar();
 19     }
 20     return ans;
 21 }
 22 ll quick_mul_mod(ll a,ll b,ll c)//a*b%c
 23 {
 24     ll ret=0;
 25     a%=c;b%=c;
 26     while(b)
 27     {
 28         if(b&1)
 29         {
 30             ret+=a;
 31             ret%=c;
 32             b--;
 33         }
 34         a<<=1;
 35         a%=c;
 36         b>>=1;
 37     }
 38     return ret;
 39 }
 40 ll gcd(ll a,ll b)
 41 {
 42     if(a==0) return 1;
 43     if(a<0) return gcd(-a,b);
 44     if(b==0)
 45     return a;
 46     return gcd(b,a%b);
 47 }
 48 ll Pollard_rho(ll x,ll c)
 49 {
 50     ll x1=rand()%(x-1)+1;
 51     ll x2=x1;
 52     int i=1,k=2;
 53     while(1)
 54     {
 55         i++;
 56         x1=(quick_mul_mod(x1,x1,x)+c)%x;
 57         ll d=gcd(x2-x1,x);
 58         if(d!=1&&d!=x) return d;
 59         if(x2==x1) return x;
 60         if(i==k)
 61         {
 62             x2=x1;
 63             k+=k;
 64         }
 65     }
 66     
 67 }
 68 ll quick_mod(ll a,ll b,ll c)//ji suan a^b%c
 69 {
 70     ll ans=1;
 71     a%=c;
 72     while(b)
 73     {
 74         if(b&1)
 75         {
 76             b--;
 77             ans=quick_mul_mod(ans,a,c);
 78         }
 79         b>>=1;
 80         a=quick_mul_mod(a,a,c);
 81     }
 82     return ans;
 83 }
 84 bool Miller_rabin(ll n)
 85 {
 86     if(n==2) return true;
 87     if(n<=1||!(n&1)) return false;
 88     ll u=n-1,t=0;
 89     while(!(u&1))
 90     {
 91         u>>=1;
 92         t++;
 93     }
 94     for(int i=0;i<S;++i)
 95     {
 96         ll x=rand()%(n-1)+1;
 97         x=quick_mod(x,u,n);
 98         for(int i=1;i<=t;++i)
 99         {
100             ll y=quick_mul_mod(x,x,n);
101             if(y==1&&x!=1&&x!=n-1)
102               return false;
103             x=y;
104         }
105         if(x!=1) return false;
106     }
107     return true;
108 }
109 void findpri(ll n)
110 {
111     if(n==1) return;
112     if(Miller_rabin(n))
113     {
114         maxz=max(maxz,n);
115         return;
116     }
117     ll p=n;
118     while(p==n)
119       p=Pollard_rho(p,rand()%(n-1)+1);
120     findpri(p);
121     findpri(n/p);
122 }
123 int main()
124 {
125     srand(time(0));
126     cas=read();
127     while(cas--)
128     {
129         maxz=0;
130         ll n=read();
131         findpri(n);
132         if(maxz==n)/*最大的质因数就是本身*/
133           printf("Prime\n");
134         else printf("%lld\n",maxz);
135     }
136     return 0;
137  }