大话卷积神经网络CNN(干货满满)
Posted 我是管小亮
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了大话卷积神经网络CNN(干货满满)相关的知识,希望对你有一定的参考价值。
声明:
1)该文章整理自网上的大牛和机器学习专家无私奉献的资料,具体引用的资料请看参考文献。
2)本文仅供学术交流,非商用。所以每一部分具体的参考资料并没有详细对应。如果某部分不小心侵犯了大家的利益,还望海涵,并联系博主删除。
3)博主才疏学浅,文中如有不当之处,请各位指出,共同进步,谢谢。
4)此属于第一版本,若有错误,还需继续修正与增删。还望大家多多指点。大家都共享一点点,一起为祖国科研的推进添砖加瓦。
文章目录
O、前言
本博客创作的主要目的,是对时下最火最流行的深度学习算法的基础知识做一个简介,本人看过许多教程,感觉对小白不是特别友好,尤其是在踩过好多坑之后,于是便有了写这篇博客的想法。本文文中会有相关部分的链接,并且在博客的最后会给出 个人推荐的学习资源,如果着急寻找资源的同学可以通过目录直接跳到最后。
一、简介
百度百科中对深度学习的定义是深度学习(DL, Deep Learning)是机器学习(ML, Machine Learning)领域中一个新的研究方向,它被引入机器学习使其更接近于最初的目标——人工智能(AI, Artificial Intelligence)。这个定义太大了,反而让人有点不懂,简答来说,深度学习就是通过多层神经网络上运用各种机器学习算法学习样本数据的内在规律和表示层次,从而实现各种任务的算法集合。各种任务都是啥,有:数据挖掘,计算机视觉,语音识别,自然语言处理等。
可能有人会问那么深度学习,机器学习还有人工智能的关系是怎么样的呢?在这个博客中有详细介绍:一篇文章看懂人工智能、机器学习和深度学习,我们这里直接拿出结论:
- AI:让机器展现出人类智力
- 机器学习:抵达AI目标的一条路径
- 深度学习:实现机器学习的技术
深度学习从大类上可以归入神经网络,不过在具体实现上有许多变化,并不像大家听到的一样,觉得这两个概念其实是同一个东西,在知乎上有相关讨论:看“深度学习”和“多层神经网络”的区别?,我们这里直接拿出结论:
- 从广义上说深度学习的网络结构也是多层神经网络的一种。更简单来说,多层神经网络 做的步骤是:特征映射到值。特征是 人工 挑选。深度学习 做的步骤是 信号->特征->值。 特征是由 网络自己 选择。
深度学习的核心是 特征学习,旨在通过分层网络获取分层次的特征信息,从而解决以往需要人工设计特征的重要难题。深度学习是一个框架,包含多个重要算法:
- Convolutional Neural Networks(CNN)卷积神经网络
- AutoEncoder自动编码器
- Sparse Coding稀疏编码
- Restricted Boltzmann Machine(RBM)限制波尔兹曼机
- Deep Belief Networks(DBN)深度信念网络
- Recurrent neural Network(RNN)多层反馈循环神经网络神经网络
对不同的任务(图像,语音,文本),需要选用不同的网络模型才能达到更好的效果。
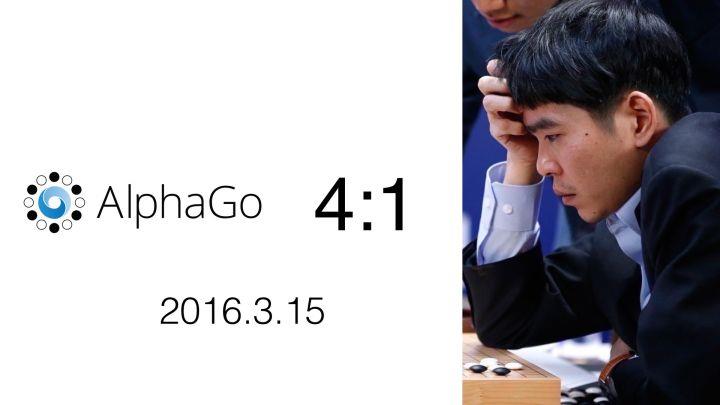
此外,最近几年 增强学习(Reinforcement Learning) 与深度学习的结合也创造了许多了不起的成果,AlphaGo就是其中之一。
大家比较关注的热点新闻,如下图所示:
图片来源:https://zhuanlan.zhihu.com/p/20893777?refer=intelligentunit
二、人类视觉原理
深度学习的许多研究成果,离不开对大脑认知原理的研究,尤其是视觉原理的研究。
1981 年的诺贝尔医学奖,颁发给了 David Hubel(出生于加拿大的美国神经生物学家) 和TorstenWiesel,以及 Roger Sperry。前两位的主要贡献,是“发现了视觉系统的信息处理”——可视皮层是分级的。如下图所示:
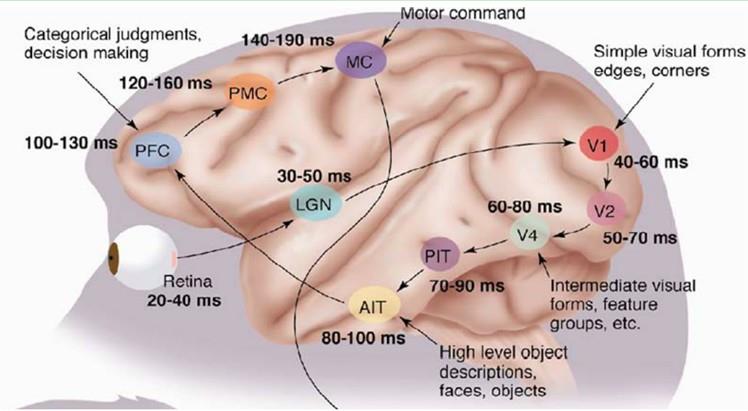
进而通过大量试验研究,发现了人类的视觉原理,具体如下:从原始信号 摄入 开始(瞳孔摄入像素 Pixels),接着做 初步处理(大脑皮层某些细胞发现边缘和方向),然后 抽象(大脑判定,眼前的物体的形状,是圆形的),然后 进一步抽象(大脑进一步判定该物体是只气球)。
下面是人脑进行人脸识别的一个示例。如下图所示:
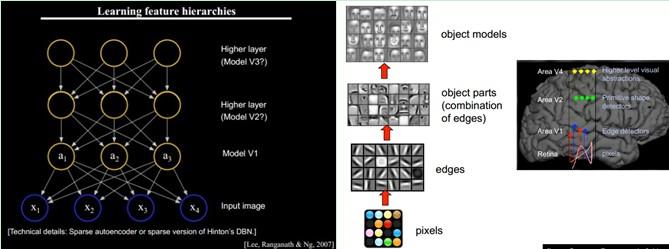
总的来说,人的视觉系统的信息处理是 分级 的。从低级的V1区 提取边缘特征,再到V2区的 形状或者目标的部分 等,再到更高层,整个目标、目标的行为 等。也就是说高层的特征是低层特征的组合,从低层到高层的特征表示越来越抽象,越来越能表现语义或者意图。而抽象层面越高,存在的可能猜测就越少,就越利于分类。
对于不同的物体,人类视觉也是通过这样 逐层分级,来进行认知的。如下图所示:

那么可以很自然的想到:可以不可以模仿人类大脑的这个特点,构造多层的神经网络,较低层的识别初级的图像特征,若干底层特征组成更上一层特征,最终通过多个层级的组合,最终在顶层做出分类呢?答案是肯定的,这也是许多深度学习算法(包括CNN)的灵感来源。
三、神经网络
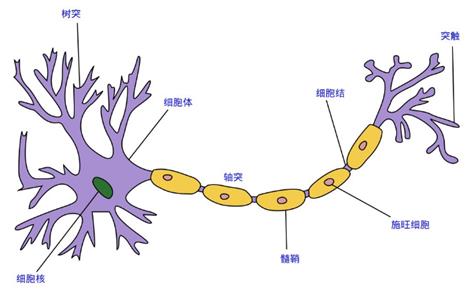
首先什么是神经网络呢?神经网络也指的是 人工神经网络(Artificial Neural Networks,简称ANNs),是一种模仿生物神经网络行为特征的算法数学模型,由 神经元、节点与节点之间的连接(突触) 所构成,如下图所示:
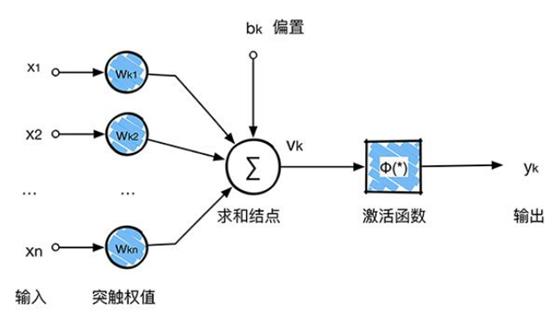
每个神经网络单元抽象出来的数学模型如下,也叫 感知器,它接收多个输入(
x
1
,
x
2
,
x
3
.
.
.
x_1,x_2,x_3...
x1,x2,x3...),产生一个输出,这就好比是神经末梢感受各种外部环境的变化(外部刺激),然后产生电信号,以便于转导到神经细胞(又叫神经元)。如下图所示:
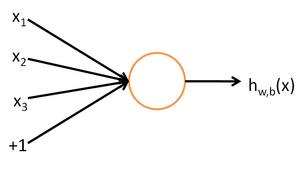
单个的感知器就构成了一个简单的模型,但在现实世界中,实际的决策模型则要复杂得多,往往是由多个感知器组成的多层网络,如下图所示,这也是经典的神经网络模型,由 输入层、隐含层、输出层 构成。如下图所示:
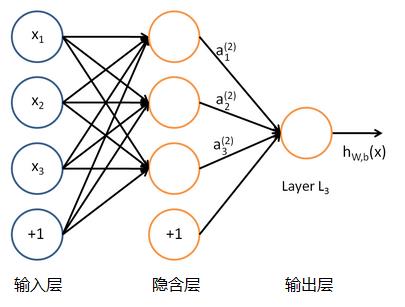
人工神经网络可以映射任意复杂的非线性关系,具有很强的鲁棒性、记忆能力、自学习等能力,在分类、预测、模式识别等方面有着广泛的应用。
四、卷积神经网络
4.1、CNN定义
主角登场,其他人退让!!!如下图所示:
重点来了,什么是卷积神经网络?
百度百科中的定义是 卷积神经网络(Convolutional Neural Networks, CNN)是一类包含卷积计算且具有深度结构的前馈神经网络(Feedforward Neural Networks),是深度学习(deep learning)的代表算法之一,擅长处理图像特别是图像识别等相关机器学习问题。
卷积网络通过一系列方法,成功将数据量庞大的图像识别问题不断降维,最终使其能够被训练。
4.2、卷积(Convolution)
卷积神经网络中的核心即为 卷积运算,其相当于图像处理中的 滤波器运算。对于一个 m × n m \\times n m×n 大小的卷积核,
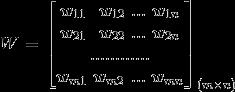
其对某一原图像
X
X
X 进行卷积运算的过程为:卷积核
W
W
W 中的每一个权值
w
w
w 分别和覆盖的原图像
X
X
X 中所对应的像素
x
x
x 相乘,然后再求和。计算公式为:
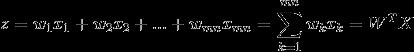
所以一幅图像的一个完整的卷积运算过程为:卷积核以一定的间隔滑动,并对所覆盖的区域进行卷积运算得到值 z,直至遍历完整幅图像。如下图所示:
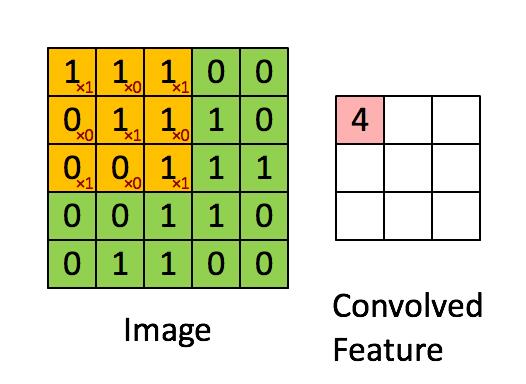
举一个标准的卷积运算例子,初始位置的计算过程是:1x1+1x0+1x1+0x0+1x1+1x0+0x1+0x0+1x1=4,详细的就不推导了。
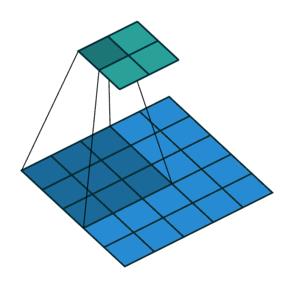
如上图,卷积核大小是3x3的,也就是说其卷积核每次覆盖原图像的9个像素,行和列都滑动了3次,一共滑动3x3=9次,得到了一个
3
×
3
3\\times 3
3×3 的二维数据。这个大小是怎么计算的呢?
首先给出结论,对于一个大小为 n n n 的原图像,经过大小为 f f f 的卷积运算后,其输出图像的尺寸为 n − f + 1 n-f+1 n−f+1。所以对于上图的例子,5-3+1=3即为所求。
4.3、步长(stride)
滑动一定的间距,但这个间距该如何定义呢? 这个概念就是卷积的 “步长”(stride)。经过步长 s s s 的操作后,其输出图像的尺寸为:
⌊ n − f s ⌋ + 1 \\left \\lfloor \\fracn-fs \\right \\rfloor +1 ⌊sn−f⌋+1
其中 n 是图像大小,f 是卷积核大小,s 是步长。
stride = 1 表示卷积核滑过每一个相距是 1 的像素,是最基本的单步滑动,作为标准卷积模式。Stride 是 2 表示卷积核的移动步长是 2,跳过相邻像素,输出图像缩小为原来的 1/2。Stride 是 3 表示卷积核的移动步长是 3,跳过 2 个相邻像素,图像缩小为原来的 1/3,以此类推。。。
详细的卷积层尺寸推算细节可以看一下这个文章——CNN中卷积层的计算细节
4.4、填充(padding)
在标准的卷积过程中,存在两个问题:
- 每次卷积运算后,图像就会缩小尺寸。在经历多次运算后,图像最终会失去其本来的形状,变为 1 × 1 1\\times 1 1×1 的 “柱状”。
- 对于图像边缘的像素,只被一个输出使用,但图像中间的像素,则被多个输出使用。这意味着卷积过程丢掉了图像边缘位置的许多信息。
对于这个问题,可以采用额外的 “假” 像素(通常值为 0, 因此经常使用的术语 ”零填充“ )填充边缘。这样,在滑动时的卷积核可以允许原始边缘像素位于其中心,同时延伸到边缘之外的假像素。假设填充的像素大小为 p p p ,则 n n n 就变成了 n + 2 p n+2p n+2p,故其输出图像的尺寸为 ⌊ n + 2 p − f s ⌋ + 1 \\left \\lfloor \\fracn+2p-fs \\right \\rfloor +1 ⌊sn+2p−f⌋+1。
至于是否选择填充像素,通常有两个选择,分别叫做 Valid 卷积和 Same 卷积。
- Valid 卷积意味着 不填充,即图像会通过卷积并逐渐缩小,输出的图像尺寸即为上述公式: ⌊ n + 2 p − f s ⌋ + 1 \\left \\lfloor \\fracn+2p-fs \\right \\rfloor +1 ⌊sn+2p−f⌋+1。
- Same卷积意味 填充,输出图像的尺寸与输入图像的尺寸相同。
根据上述尺寸的计算公式,令 ⌊ n + 2 p − f s ⌋ + 1 = n \\left \\lfloor \\fracn+2p-fs \\right \\rfloor +1=n ⌊sn+2p−f⌋+1=n,可得到 p = ( n − 1 ) s − n + f 2 p=\\frac(n-1)s-n+f2 p=2(n−1)s−n+f。当 s=1 时, p = f − 1 2 p=\\fracf-12 p=2f−1。
4.5、池化(Pooling)
随着模型网络不断加深,卷积核越来越多,要训练的参数还是很多,而且直接拿卷积核提取的特征直接训练也容易出现过拟合的现象。CNN使用的另一个有效的工具被称为“池化(Pooling)”出现并解决了上面这些问题,为了有效地减少计算量,池化就是将输入图像进行缩小,减少像素信息,只保留重要信息;为了有效地解决过拟合问题,池化可以减少数据,但特征的统计属性仍能够描述图像,而由于降低了数据维度,可以有效地避免过拟合。
给出池化的定义,对不同位置区域提取出有代表性的特征(进行聚合统计,例如最大值、平均值等),这种聚合的操作就叫做 池化,池化的过程通常也被称为 特征映射 的过程(特征降维)。听起来很高深,其实简单地说就是下采样。
池化的过程如下图所示:
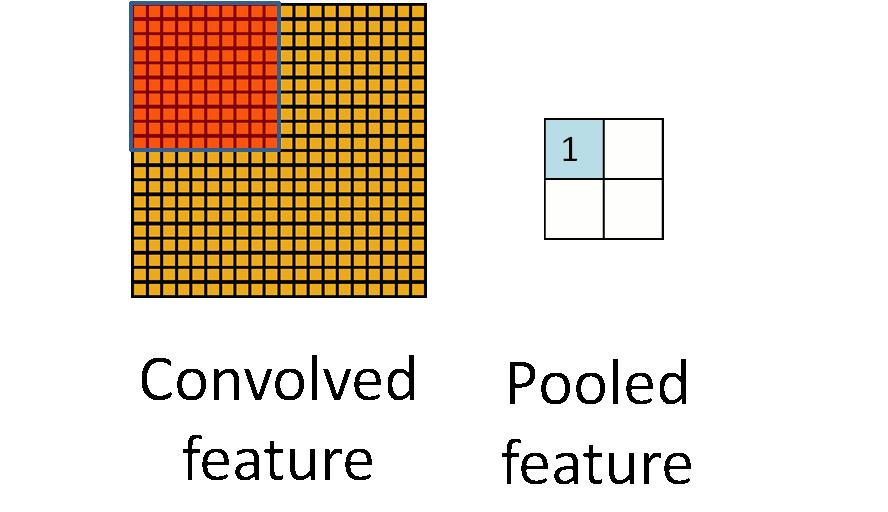
池化主要有两种,除了 最大值池化(Max Pooling) 之外,还有 平均值池化(Average pooling),CNN中随机池化使用的较少。
最大池化是对局部的值取最大;平均池化是对局部的值取平均;随机池化是根据概率对局部的值进行采样,采样结果便是池化结果。概念非常容易理解,其示意图如下所示: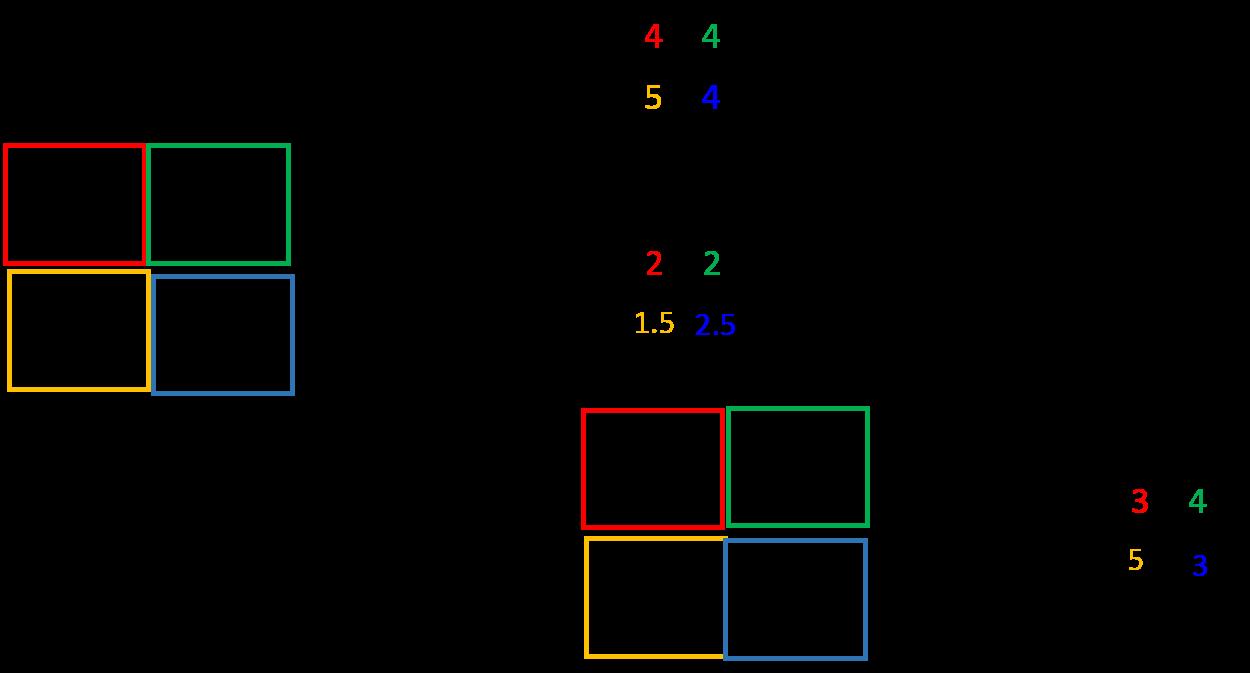
三种池化的意义:
- 最大池化可以获取局部信息,可以更好保留纹理上的特征。如果不用观察物体在图片中的具体位置,只关心其是否出现,则使用最大池化效果比较好。
- 平均池化往往能保留整体数据的特征,能凸出背景的信息。
- 随机池化中元素值大的被选中的概率也大,但不是像最大池化总是取最大值。随机池化一方面最大化地保证了Max值的取值,一方面又确保了不会完全是max值起作用,造成过度失真。除此之外,其可以在一定程度上避免过拟合。
4.6、激活函数
回顾一下感知机,感知机在接收到各个输入,然后进行求和,再经过激活函数后输出。为什么神经网络需要非线性激活函数?
为了使神经网络能够拟合出各种复杂的函数,必须使用 非线性激活函数,用来加入非线性因素,把卷积层输出结果做非线性映射。
在神经网络的正向传播过程中
(
Z
[
l
]
=
W
[
l
]
A
[
l
−
1
]
+
b
[
l
]
,
A
[
l
]
=
g
(
Z
[
l
]
)
)
(Z^[l]=W^[l]A^[l-1]+b^[l], A^[l]=g(Z^[l]))
(Z[l]=W[l]A[l−1]+b[l],A[l]=g(Z[l])),如果我们去掉激活函数
g
g
g,则
A
[
l
]
=
Z
[
l
]
A^[l]=Z^[l]
A[l]=Z[l],这个有时被叫做 线性激活函数(更学术点的名字是 恒等激励函数,因为它们就是把输入值恒等地输出),具体公式如下:
第一层: A [ 1 ] = Z [ 1 ] = W [ 1 ] X + b [ 1 ] A^[1]=Z^[1]=W^[1]X+b^[1] A[1]=Z[1]=W[1]X+b[1]
第二层: A [ 2 ] = Z [ 2 ] = W [ 2 ] A [ 1 ] + b [ 2 ] A^[2]=Z^[2]=W^[2]A^[1]+b^[2] A[2]=Z[2]=W[2]A[1]+b[2]
将 A [ 1 ] A^[1] A[1] 带入可得第二层: A [ 2 ] = Z [ 2 ] = W [ 2 ] ( W [ 1 ] X + b [ 1 ] ) + b [ 2 ] = W [ 2 ] W [ 1 ] X + W [ 2 ] b [ 1 ] + b [ 2 ] A^[2]=Z^[2]=W^[2](W^[1]X+b^[1])+b^[2]=W^[2]W^[1]X+W^[2]b^[1]+b^[2] A[2]大话卷积神经网络CNN,小白也能看懂的深度学习算法教程,全程干货建议收藏!